RS码编码参数的盲识别*
张立民,刘 杰
(1.海军航空工程学院 信息融合研究所,山东 烟台 264001;2.解放军91640部队,广东 湛江 524054;3.航天恒星科技有限公司,北京 100086)
RS码编码参数的盲识别*
张立民1,刘 杰**
(1.海军航空工程学院 信息融合研究所,山东 烟台 264001;2.解放军91640部队,广东 湛江 524054;3.航天恒星科技有限公司,北京 100086)
针对现有的RS(Reed-Solomon)码盲识别计算复杂度较大的问题,提出了一种新的识别方法。首先统计不同码长分组时的码重分布,并定义与理论码重分布之间的相似度系数,通过计算找出最相似的一组即对应正确的码长;然后建立二元假设,并确定判决门限对码根进行判定;通过遍历域内所有的本原多项式,找出完整的连续码根分布,进而完成生成多项式的识别。仿真结果表明,所提方法的计算量较其他方法明显减少,并能有效完成码长和生成多项式的识别,在误码率小于10-3时,对常用RS码的识别率能达到90%以上。
信道编码;RS码;盲识别;码重分布;连续码根
1 引 言
信道编码是为了抵抗信息传输过程中的干扰和噪声而人为加入的冗余。随着现代数字通信系统的发展,信道编码盲识别在自适应调制编码(Adaptive Modulation and Coding,AMC)技术和非协作条件下的通信侦察领域应用广泛,并迅速成为了一个新的研究热点[1-3]。
RS码是多进制BCH(Bose-Chaudhuri-Hocquenghem)码的一个重要子类,它具有纠错能力强、编码结构简单等特点,被广泛应用于各种通信系统中[4]。因此,对RS 码的盲识别进行研究具有重要意义。目前,见于文献的相关方法主要有矩阵分析法、码根统计法和基于伽罗华域傅里叶变换(Galois Field Fourier Transform,GFFT)的方法。文献[5]利用矩阵秩差识别码长,并引入熵函数差值识别本原多项式。文献[6]利用矩阵秩函数识别 RS 码的二进制衍生码长,采用码根统计完成生成多项式的识别。文献[7]将GFFT用于域的本原多项式求解,在此基础上,文献[8]提出了在GFFT后进行频谱累积量统计的检测方法。文献[9]使用非线性变换和中值滤波来充分利用频谱的统计信息,文献[10]引入了衡量谱分量概率分布差异性的欧几里德距离测度。以上方法均需要对码长和本原多项式进行验证,当码长较大时,运算量也随之增大。
针对以上存在的不足,本文提出了一种新的RS码盲识别方法:首先根据RS码的码字重量满足固定分布这一特性,对码长进行识别;然后建立二元假设对码根和本原多项式进行判定,进而完成对生成多项式的识别。
2 问题描述
定义1[11]GF(q)上(q≠2)码长n=q-1的本原 BCH码称为RS码。
在RS码作为差错控制的所有实际应用中,q都设置为2m,并且码符号均取自伽罗华域GF(2m)。对符号取自GF(2m)、信息位长度为k且纠t个错误的RS码,其满足n-k=2t,码最小距离d=2t+1。令α为GF(2m)中的本原元,则其生成多项式g(X)以α,α2,…,α2t为其全部根。由于αi是GF(2m)中的元素,因此其最小多项式即为X-αi。于是,
g(X)=(X-α)(X-α2)…(X-α2t)=g0+g1X+g2X2+…+g2t-1X2t-1+X2t。
(1)
其中:gi∈GF(2m),0≤i<2t,且gi≠0。其奇偶校验矩阵具有如下形式:
(2)
在实际应用中,通过帧同步分析,可以很容易确定RS码的码字起点。在此条件下,需要识别的参数包括码长,编码域对应的本原多项式及生成多项式。
3 RS码盲识别实现
3.1 基于码重统计的码长识别
RS码在实际数字通信系统中以二进制形式进行传输,接收的序列为GF(2m)码元在GF(2)上映射得到的二进制准循环码,其码长为(2m-1)m,码元之间的映射关系由选取的本原多项式决定。以GF(8)为例,表1给出了p1(X)=1+X+X3和p2(X)=1+X2+X3两种情况下GF(8)到GF(2)映射情况。可以看出,GF(2)中“00…0”始终对应GF(2m)中“0”,因此在统计码重时,并不需要考虑实际采用的本原多项式和映射情况,只需以长度(2m-1)×m划分码字,每个码字内按m位比特进行遍历,只要不出现连续全零状态,则码重加1。

表1 GF(8)到GF(2)映射关系Tab.1 Mapping relation from GF(8) to GF(2)
距离比奇偶校验符号数多1的编码称为极大最小距离可分(Maximum Distance Separable,MDS)码。MDS码的码重量分布有如下定理:
定理1[12]GF(q)上[n,k,d=n-k+1]MDS码中重量为i的码字个数为

(3)
RS码构成最重要的一类MDS码,显然其码重量分布也满足上述关系。因此,按可能的码长逆映射得到RS码序列并统计其码重分布,然后根据统计结果估计合适的纠错个数t,由式(3)得到理论码重分布。两者进行对比,符合度最高的则对应正确码长。


(4)
式中:Cov()表示协方差,D()表示方差。定义相似度系数

(5)
当γ最小时,即对应正确码长。
3.2 基于连续码根判定的生成多项式识别
识别出码长后,需要在不同本原多项式下逆映射得到可能的RS编码序列,然后以每个码字为一行,分别建立码字矩阵。设建立的M行n列码字矩阵为V,根据校验关系,有
V·HT=0。
(6)
令vj=(vj,0,vj,1,…,vj,n-1)是矩阵V第j行,hi=(1,αi,α2i,…,α(n-1)i)是矩阵H第i行,由vj·(hi)T=0得
vj(αi)=vj,0+vj,1αi+vj,2α2i+…+vj,n-1α(n-1)i=0,
(7)
可知αi是码多项式
vj(X)=vj,0+vj,1X+vj,2X2+…+vj,n-1Xn-1
(8)
的根。因此,定义二元假设

(9)
然后建立关于αi的统计量,并确定其在两种假设下的概率分布,设定相应判决门限。当统计量大于该门限时,αi为矩阵V中码字的公共根,也即生成多项式g(X)的根。
根据文献[13],GF(2m)上首系数为1的m次本原多项式个数可以由公式c=φ(2m-1)/m求得,其中φ()为欧拉函数。找出所有码字连续偶数个公共码根最多时的情形,即对应正确的本原多项式。
令Mz为矩阵V中满足v(αi)=0的码字个数。在本原多项式p(X)下,若αi不是生成多项式g(X)的根,则根据文献[14],v(αi)=0的概率为pi,1=1/2m,此时Mz服从伯努利分布B(M,pi,1)。令h=Mz/M,当M足够大时,h趋于高斯分布,其概率密度函数为
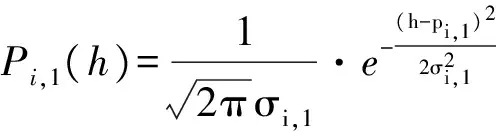
(10)


(11)
根据最小错误概率准则,定义最优判决门限

(12)则当计算出的h满足h>ηopt时,可以判定αi是所有码字多项式的公共根。经计算可得到ηopt的解析值为
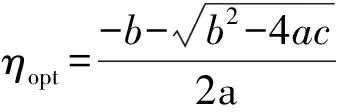
(13)
其中:
a=(1-pi,1)(1-pe)n·[2pi,1+(1-pi,1)(1-pe)n-1]/M,
(14)
b=-2pi,1(1-pi,1)(1-pe)n·[(1-pi,1)(1-pe)n+pi,1]/M,
(15)
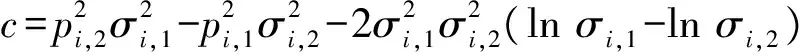
(16)
对于本原多项式p(X),设对应本原元为α,若α不满足判决门限,则说明该本原多项式不符合要求,需要选取新的本原多项式重复验证步骤;反之,若α是生成多项式g(X)的根,则对αi(i=2,3,…)依次进行验证。如果某个本原多项式从α开始存在的连续偶数个根最多,则该多项式对应正确的编码域。在确定生成多项式的连续码根分布及本原多项式后,按式(1)即可得到g(X)。
完整识别过程的流程如图1所示。
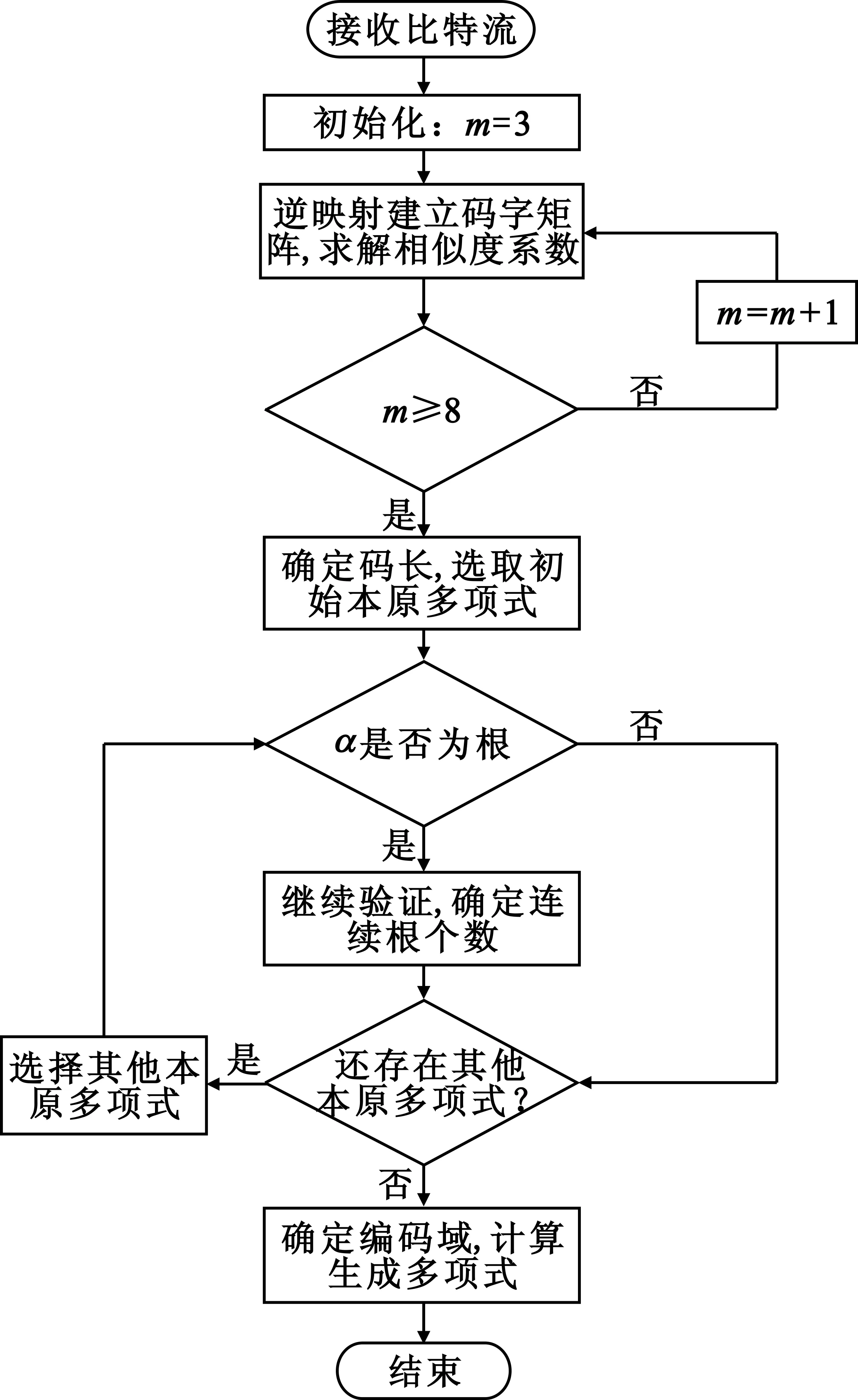
图1 识别流程图
4 仿真验证
仿真分为三部分,首先对所提方法的可行性进行研究,分别对码长和生成多项式的识别进行仿真验证,然后分析了在不同码长下的识别性能,并与其他文献中的方法进行了对比。由于RS码的性能随码长的增加而降低,实际一般使用中短码,m取3~8;同时,实际通信系统中误码率一般为10-6~10-2。因此,进行仿真时采用的编码参数、误码率均在此范围内选取。
4.1 码长识别仿真
以(31,21)RS码为研究对象,选取本原多项式为p(X)=1+X2+X5。首先随机生成0、1随机序列,然后以上述编码参数进行编码,按pe=0.001加入误码,最后得到长度为2.04×106的编码序列。在m为3~8下,按(2m-1)m进行分组,取N=1 000,并选择任意的本原多项式将二元码字映射为GF(2m)中的码字,然后对码字的重量分布进行统计,结果如表2所示(由于篇幅所限,仅列出重量分布中不为0的最后几位)。

表2 不同m值下码重分布统计结果Tab.2 Statistic result of code weight under different m
利用式(5)对相似度系数进行计算,结果如图2所示。
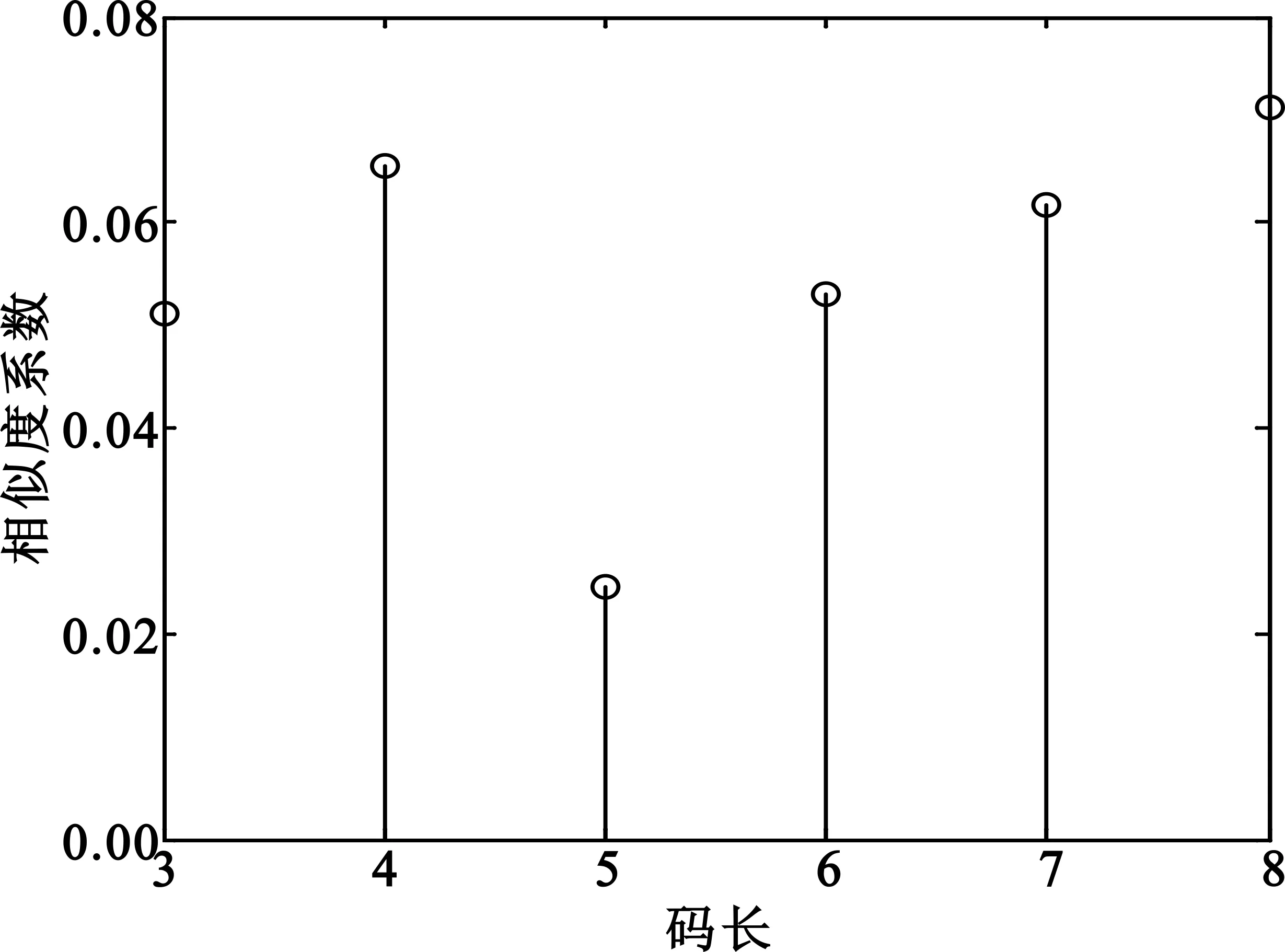
图2 码长识别结果
由图2可以看出,当m为3、4、6、7和8时,由于编码域错误,所得到的码组并不是真实码字,因此其重量分布与理论值相差较大,造成相似系数偏大。当m=5、对应码长n=31时相似度系数最小,因此该处即为正确码长,与实际情况相符。
4.2 生成多项式识别仿真
下面对本原多项式和生成多项式进行识别,仿真条件与上面相同。m=5对应6个本原多项式,分别为p1(X)=1+X2+X5、p2(X)=1+X3+X5、p3(X)=1+X+X2+X3+X5、p4(X)=1+X+X2+X4+X5、p5(X)=1+X+X3+X4+X5和p6(X)=1+X2+X3+X4+X5,在Matlab软件中用十进制分别表示为37、41、47、55、59和61。取M=200,用本原元α对6种本原多项式进行判决,结果如表3所示。可以看出,仅在37处,所得到的h值大于判决门限,因此编码域对应的本原多项式为p1(X)=1+X2+X5,与实际相符。
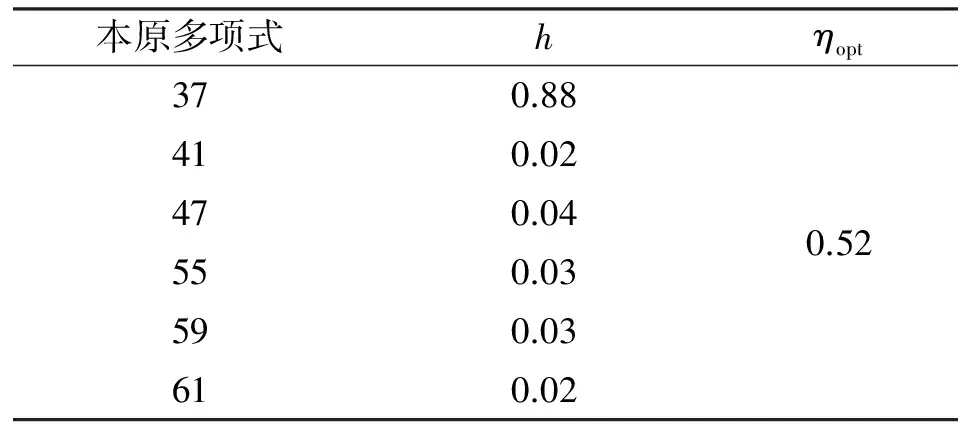
表3 本原根α判定结果Tab.3 Judgment result of primitive element α
然后对除了α以外的其他根进行判定,结果如表4所示。可以看出,α2~α10均符合要求,而从α11开始,计算得到的h值小于判决门限,因此2t=10,k=n-2t=21,与实际相符。对应生成多项式为
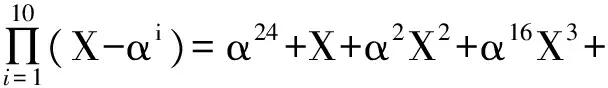
至此,整个识别过程结束。
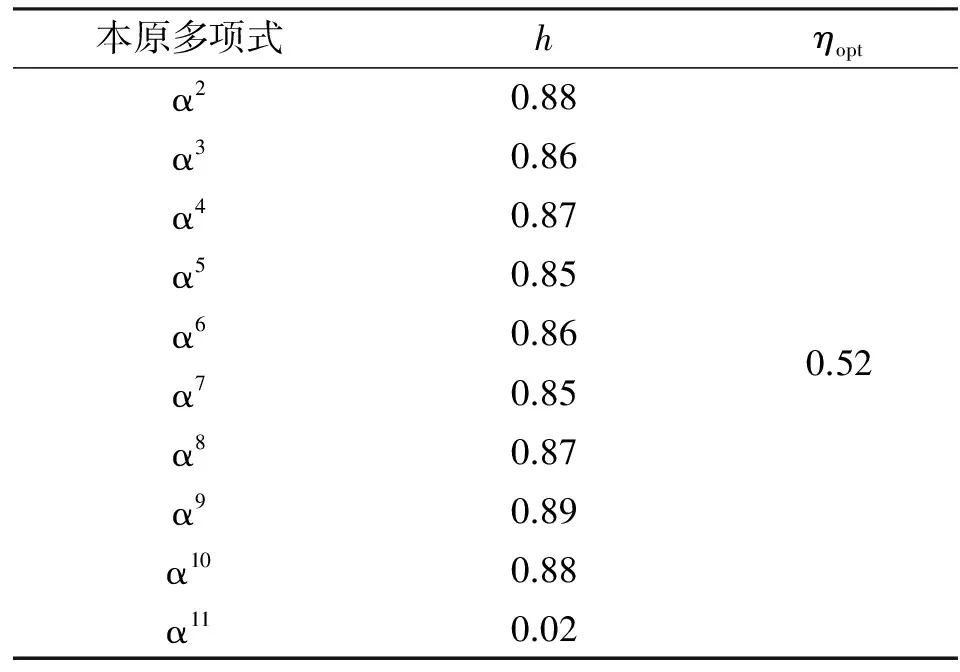
表4 其他码根判定结果Tab.4 Judgment result of other code roots
4.3 识别性能分析
图3给出了m等于5~8四种情况下识别概率随误码率变化的曲线,选取的具体RS码分别为(31,21)码、(63,51)码、(127,113)码和(255,223)码。可以看出,码长越大,识别概率越低。在误码率小于10-3时,对所有码型的识别概率都能达到90%。
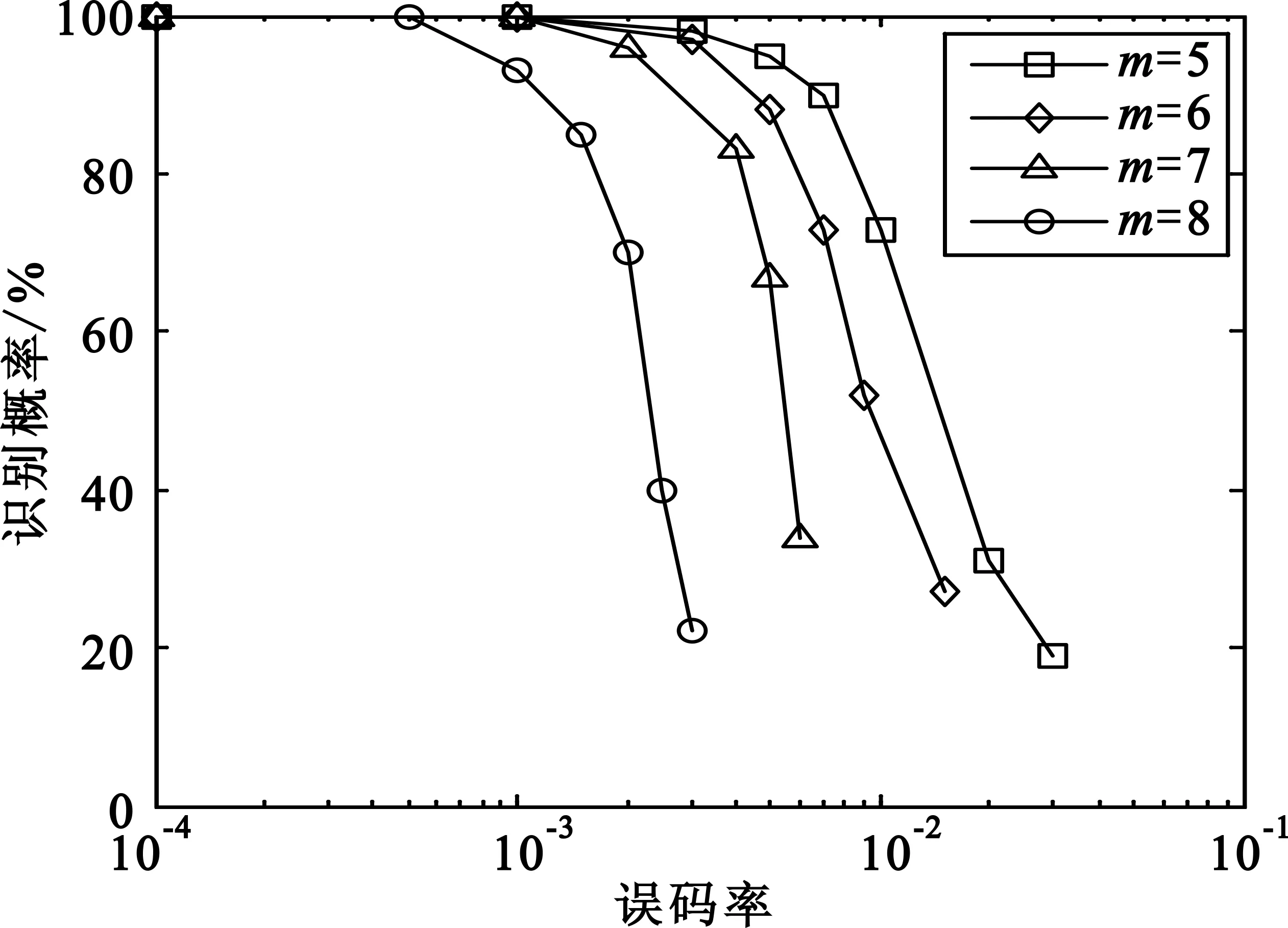
图3 不同码长RS码识别结果
将本文方法与文献[6]中矩阵分析结合码根统计的方法、文献[7]中基于GFFT的方法进行性能对比,对(31,21)RS码进行识别,结果如图4所示。由图可见本文方法略优于文献[6]中的方法,但逊于文献[7]中的方法。原因在于,文献[6]进行矩阵分析时,初等变换的过程会造成错误传播,且进行码根统计时未定义判决门限,因此其抗误码性能比本文差。文献[7]采用变换域方法,通过遍历本原多项式和码长完成识别,在牺牲计算复杂度的前提下获得较好的性能。

图4 识别性能对比
最后,对3种方法的计算复杂度进行分析。本文中,求单个码字码重的计算复杂度为mn,验证元素是否为码字多项式根需要n-1次GF(2m)域乘法和加法,转换到二元域的计算复杂度为(n-1)·[3m(m-1)+m];设文献[6]中识别码长时每个m值下验证1 000次,则矩阵分析需进行500(mn-1)mn次行模2加运算,验证码根的计算复杂度与本文相同;文献[7]中一次GFFT需n2次GF(2m)域乘法和n2-n次GF(2m)域加法,换算到二元域的计算复杂度为3m2n2-2mn2-mn[15]。取N=1 000,M=5n,上述3种方法的理论计算复杂度如图5所示。可以看出,本文方法计算复杂度明显小于其他两种方法,结合图4,说明本文方法适用于低误码率情况下的识别。
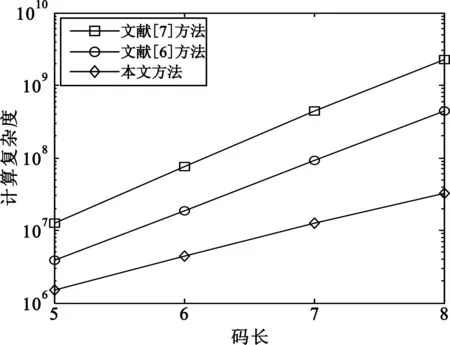
图5 计算复杂度对比
5 结 论
根据RS码的编码结构和特性,本文提出了一种新的RS码盲识别方法,首先给出了基于码重分析的码长识别模型,然后通过搜寻连续码根分布对本原多项式和生成多项式进行识别。与传统方法相比,本文方法能在低误码率(小于10-3)下有效完成对常用RS码的识别,且计算复杂度明显得到降低,因此适用于对实时性要求较高的系统。在后续研究中,需要进一步提升方法在高误码率下的性能。
[1] XIA T,WU H C. Novel blind identification of LDPC codes using average LLR of syndrome a posteriori probability[J].IEEE Transactions on Signal Processing,2014,62(3):632-640.
[2] CHEN W,WU G Q. Blind recognition of(n-1)/n rate punctured convolutional encoders in a noisy environment[J].Journal of Communications,2015,10(4):260-267.
[3] YARDI A D,VIJAYAKUMARAN S,KUMAR A. Blind reconstruction of binary cyclic codes from unsynchronized bit stream[J].IEEE Transactions on Communications,2016,64(7):2693-2706.
[4] LIN S,COSTELLO D J. Error control coding[M].2nd ed. New Jersey,USA:Prentice Hall,2005:158-161.
[5] 李灿,张天琪,刘瑜. 基于伽罗华域高斯列消元法的 RS码盲识别[J].电讯技术,2014,54(7):926-931. LI Can,ZHANG Tianqi,LIU Yu. Blind recognition of RS codes based on Galois field columns Gaussian elimination[J].Telecommunication Engineering,2014,54(7):926-931.(in Chinese)
[6] 闻年成,杨晓静. RS码的盲参数识别[J].计算机工程与应用,2011,47(19):136-139. WEN Niancheng,YANG Xiaojing. Blind recognition of RS codes parameters[J].Computer Engineering and Applications,2011,47(19):136-139.(in Chinese)
[7] 刘健,谢锘,周希元. RS码的盲识别方法[J].电子科技大学学报,2009,38(3):363-367. LIU Jian,XIE Nuo,ZHOU Xiyuan. Blind recognition method of RS coding[J].Journal of University of Electronic Science and Technology of China,2009,38(3):363-367.(in Chinese)
[8] 王丰华,解辉,黄知涛,等. 基于频谱累积量的线性分组码检测识别方法[J].系统工程与电子技术,2013,35(12):2595-2599. WANG Fenghua,XIE Hui,HUANG Zhitao,et al.Blind recognition of linear block code based on spectral cumulants[J].Systems Engineering and Electronics,2013,35(12):2595-2599.(in Chinese)
[9] 解辉,王丰华,黄知涛,等. 基于频谱预处理的RS码盲检测识别方法[J].宇航学报,2013,34(1):128-132. XIE Hui,WANG Fenghua,HUANG Zhitao,et al.Blind detection and recognition of RS code based on spectral preprocessing[J].Journal of Astronautic,2013,34(1):128-132.(in Chinese)
[10] 包昕,陆佩忠,游凌. 基于伽罗华域傅里叶变换的RS码识别方法[J].电子科技大学学报,2016,45(1):30-35. BAO Xin,LU Peizhong,YOU Ling. Recognition of RS coding based on Galois field Fourier transform[J].Journal of University of Electronic Science and Technology of China,2016,45(1):30-35.(in Chinese)
[11] 王新梅,肖国镇. 纠错码——原理与方法[M].西安:西安电子科技大学出版社,2006:259-262.
[12] MACWILLIAMS F J,SLOANE N J A. The theory of error-correcting codes[M].New York:North-Holland Publishing Company,1977:320-321.
[13] 陈鲁生,沈世镒. 编码理论基础[M].北京:高等教育出版社,2005:37- 58.
[14] 王平,曾伟涛,陈健,等. 一种利用本原元的快速RS码盲识别算法[J].西安电子科技大学学报(自然科学版),2013,40(1):105-110. WANG Ping,ZENG Weitao,CHEN Jian,et al.Fast blind recognition algorithm for RS codes by primitive element[J].Journal of Xidian University(Natural Science Edition),2013,40(1):105-110.(in Chinese)
[15] 解辉,黄知涛,王丰华. 信道编码盲识别技术研究进展[J].电子学报,2013,41(6):1166-1173. XIE Hui,HUANG Zhitao,WANG Fenghua. Research progress of blind recognition of channel coding[J].Acta Electronica Sinca,2013,41(6):1166-1173.(in Chinese)
Blind Parameter Recognition of RS Codes
ZHANG Limin,LIU Jie1,SUN Yongwei2,ZHAO Zhimei3
(1.Research Institute of Information Fusion,Naval Aeronautical and Astronautical University,Yantai 264001,China;2.Unit 91640 of PLA,Zhanjiang 524054,China;3.Space Star Technology Co.,Ltd.,Beijing 100086,China)
As the existing methods for Reed-Solomon(RS) codes recognition are very complicated,a new method is proposed. Firstly,code weight distribution under different block length is counted. By defining similarity coefficient to the theoretical code weight,the most similar one is found,which corresponds to the correct code length. Then binary hypothesis test is established with a decision threshold to find code roots. By traversing all the primitive polynomials in the field,the complete distribution of continuous code roots is found,with which generator polynomial is calculated. Simulation results show that the computation cost of this method is significantly less than that of other methods,and it can effectively complete the recognition of code length and generator polynomial which has a recognition probability of 90% for the commonly used RS codes when the bit error rate is less than 10-3.
channel coding;RS codes;blind recognition;code weight distribution;continuous code roots
10.3969/j.issn.1001-893x.2017.06.006
张立民,刘杰,孙永威,等.RS码编码参数的盲识别[J].电讯技术,2017,57(6):650-655.[ZHANG Limin,LIU Jie,SUN Yongwei,et al.Blind parameter recognition of RS codes[J].Telecommunication Engineering,2017,57(6):650-655.]
2016-10-19;
2016-12-23 Received date:2016-10-19;Revised date:2016-12-23
国家自然科学基金重大研究计划项目(91538201);山东省“泰山学者”建设工程项目(ts201511020)
TN911.2
A
1001-893X(2017)06-0650-06
张立民(1966—),男,辽宁开原人,2005年于天津大学获博士学位,现为教授、博士生导师,主要研究方向为卫星信号处理及应用;
Email:iamzlm@163.com
刘 杰(1990—),男,湖北宜昌人,博士研究生,主要研究方向为现代信号处理技术及应用;
Email:iamliu1573@163.com
孙永威(1979—),男,山东威海人,工程师,主要研究方向为电路与系统;
赵志梅(1981—),女,北京人,工程师,主要研究方向为航测遥感。
**通信作者:iamliu1573@163.com Corresponding author:iamliu1573@163.com1,孙永威2,赵志梅3

