利用Kalman滤波修正卫星导航差分RTK定位坐标*

熊 杰

(中国西南电子技术研究所，成都 610036)



利用Kalman滤波修正卫星导航差分RTK定位坐标*

熊 杰**

(中国西南电子技术研究所，成都 610036)

卫星导航差分RTK(Real Time Kinematic)定位方法的定位精度极易受到载波相位整周模糊度固定算法的影响，在模糊度固定失败的情况下，差分RTK定位将出现大幅偏差。针对该问题，基于Jerk模型提出了一种利用Kalman滤波修正差分RTK定位坐标的方法。在传统Jerk模型基础上，将卫星导航系统输出的载体运动速度信息引入状态空间模型的观测方程。基于扩展状态空间模型，利用Kalman滤波器实时修正载体的位置坐标。半实物仿真表明，所提方法能大幅改善卫星导航差分RTK定位精度。

全球卫星导航系统；RTK技术；Jerk模型；Kalman滤波

1 引 言

卫星导航差分RTK(Real Time Kinematic)技术具有高精度实时定位能力，越来越多地应用到飞行器编队飞行、无人机着陆、空中加油、电力、水利、数据链时间同步、CORS网、遥感测绘等诸多技术领域[1-4]。但是，卫星导航差分RTK技术高精度定位能力的获得是以载波相位整周模糊度固定成功为基础的。针对现有常见的载波相位整周模糊度固定算法[5-8]，文献[9-11]对载波相位整周模糊度固定成功概率进行的研究结果表明，现有的载波相位整周模糊度固定算法的固定成功率均不能达到100%，而当载波相位整周模糊度固定失败时，其定位精度将大大恶化[9]。这也就意味着，在某些场合，像飞行器编队飞行、无人机着陆、空中加油这样的应用中，存在着因定位精度恶化而导致的载体飞行安全风险。这就需要对卫星导航差分RTK技术给出的定位结果进行进一步的修正，提高其实时定位精度，从而提高导航系统的可靠性。

针对这一技术需求，在分析卫星导航差分RTK技术的原理上，本文提出了一种基于Kalman滤波的卫星导航差分RTK定位坐标修正算法。该方法基于卫星导航接收机的多普勒观测能力，将载体运动速度信息引入Jerk模型[12-13]，增加状态空间模型的观测方程个数，利用Kalman滤波器实时修正卫星导航差分RTK技术给出的载体坐标，从而提高导航系统的定位精度。半实物仿真实验的结果表明，文中提出的修正方法能大幅改善卫星导航差分RTK定位精度。

2 卫星导航差分RTK定位坐标Kalman滤波修正算法

卫星导航差分RTK定位的核心是载波相位整周模糊度固定算法。常用算法有模糊度搜索滤波器法(Fast Ambiguity Search Filter,FAST)[5]、基于矩阵LDLT和UDUT分解的模糊度固定法[6]、最小二乘模糊度降相关平方差(Least Square Ambiguity Decorrelation Adjustment,LAMBDA)法[7-8]，其中LAMBDA算法被公认为固定整周模糊度最有效的方法。本节在分析LAMBDA算法原理的基础上，提出卫星导航差分RTK定位坐标Kalman滤波修正算法。

2.1 LAMBDA算法基本原理

假设卫星导航系统基站与差分站共视k+1颗卫星，不妨以单频GNSS接收机为例，线性化后的载波相位双差观测方程如下[14]：

ξ=Aη+BN+v。

(1)

式中：ξ∈2k为载波相位双差观测值与伪距双差观测值构成的向量，η∈3表示基线向量，N∈k表示载波相位双差整周模糊度向量，v∈2k表示观测噪声，A∈2k×3表示基线常系数矩阵，B∈2k×k表示模糊度常系数矩阵。方程中的未知量既涉及实数型变量η又涉及整数型变量N，因此一般按照以下3个步骤求解载波相位双差观测方程[14]:

第一步，利用最小二乘求解η和N的浮点解，即

(2)

第二步，固定模糊度浮点解，即

(3)

(4)

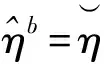
文献[9-11]相继研究了模糊度固定LAMBDA算法的成功概率，结果表明LAMBDA算法并不能完全正确地估计载波相位整周模糊度。根据工程经验，载波相位模糊度固定失败会使得RTK定位出现米级甚至数十米级的定位偏差。这种数量级的定位偏差已不再适合对定位精度要求苛刻的应用场合，如飞行器编队飞行、无人机着陆、空中加油等。因此，有必要实时地修正差分RTK定位坐标，以提高导航系统的可用性、连续性以及可靠性。

2.2 卫星导航差分RTK定位坐标Kalman滤波修正算法

从上节的分析可知，卫星导航差分RTK定位坐标有时会出现大幅偏差，一个很重要的原因是求解方程过程中忽略了卫星导航接收机输出的多普勒观测量。多普勒观测量与速度相关，通过标准最小二乘技术可将多普勒观测量转化为运动载体的速度[14]。一旦多普勒观测量转化成载体速度，即可使用Kalman滤波器实时修正载体位置。本节余下部分将讨论如何将由多普勒观测量估计的差分站速度引入Jerk模型，并基于扩展Jerk模型使用Kalman滤波器实时修正卫星导航差分RTK定位坐标。

Jerk模型由文献[12]首次提出，该模型首次将载体运动的加加速度引入状态方程。文献[13]给出了采样周期T≪1时，该模型的简化表述形式。具体地，对于位于坐标φ的载体，其状态向量定义为

(5)

当采样周期为T≪1，那么载体运动的状态空间模型为

(6)

其中：

(7)

(8)

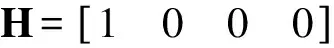
(9)

(10)

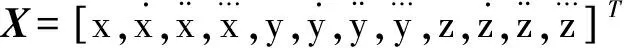
(11)

观测向量Z具有如下形式：

(12)

那么，差分站的增广Jerk模型具有如下状态空间描述：

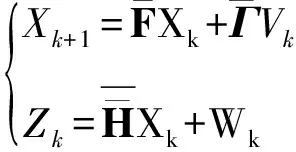
(13)

其中，系数矩阵具有如下形式：

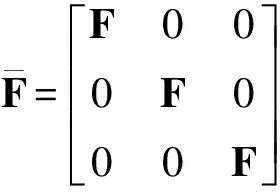
(14)

(15)

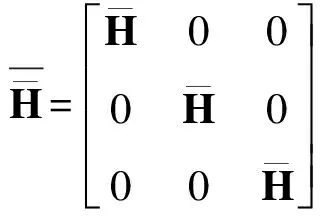
(16)

假设过程噪声Vk为三维零均值高斯白噪声，协方差矩阵为Q；测量噪声Wk为6维零均值高斯白噪声，协方差矩阵为R；假设过程噪声Vk与测量噪声Wk统计独立。

基于状态空间模型，卫星导航差分RTK定位坐标Kalman滤波修正算法递推关系如下：

(17)

3 半实物仿真实验

本文在半实物仿真环境下验证所提卫星导航差分RTK定位坐标Kalman滤波修正算法性能。仿真原理框架如图1所示，仿真环境如图2所示。

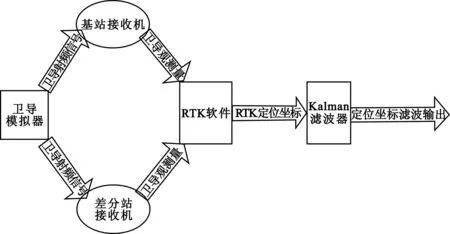
图1 仿真原理框图

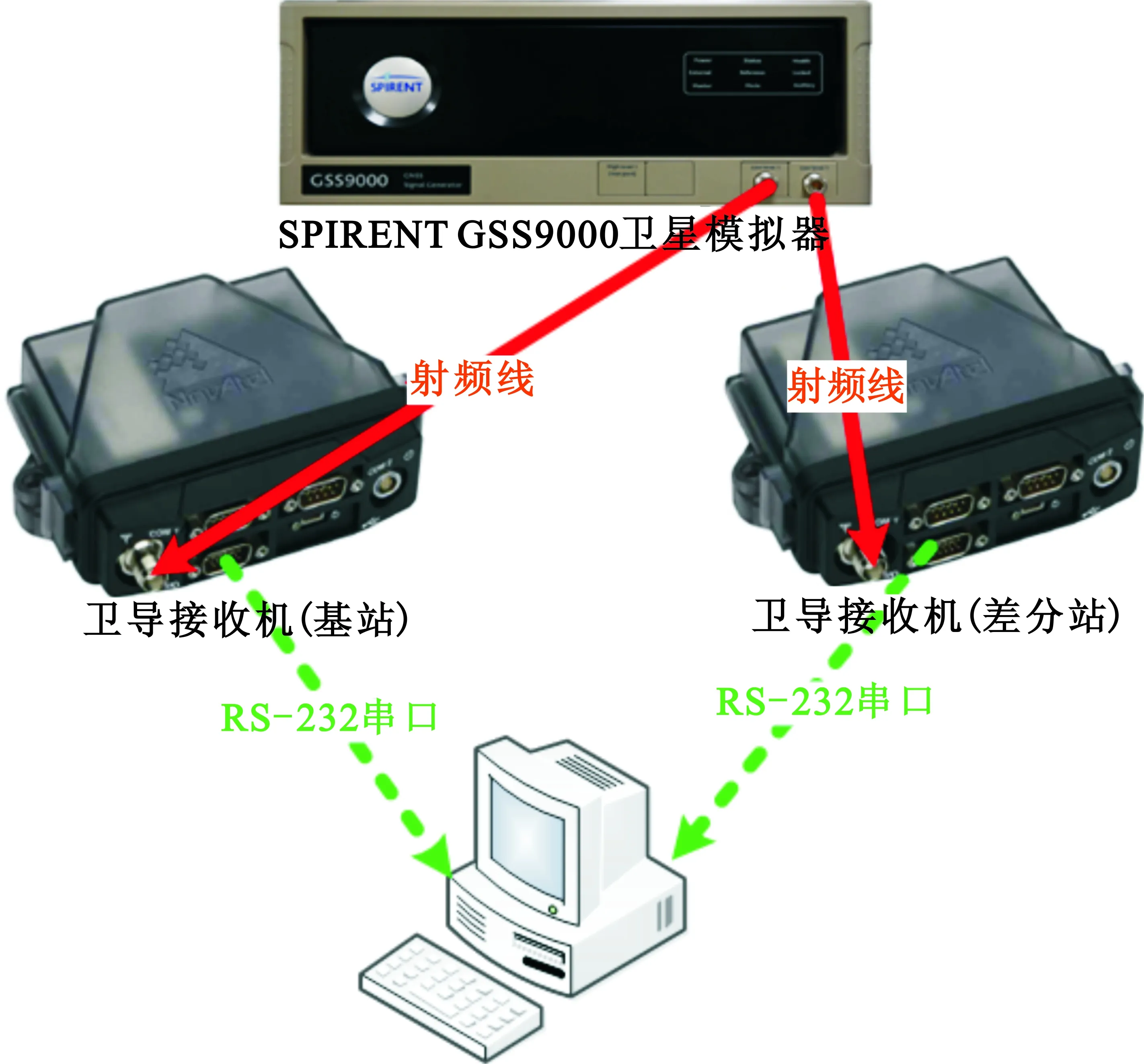
图2 GNSS半实物仿真环境

在图1所示的仿真原理框图中，卫导模拟器不仅能模拟GNSS导航星座播发的卫导射频信号，而且还能同时模拟卫星导航系统基站与差分站的运动轨迹，以及运动轨迹每一点上基站与差分站的GNSS接收机天线收到的卫星导航射频信号；基站卫星导航接收机和差分站卫星导航接收机收到卫星导航模拟器发出的射频信号后产生卫星导航观测量；运行在计算机上RTK定位软件以RS-232串口方式接收基站和差分站发出的卫星导航观测量后实时进行RTK定位，并向Kalman滤波器输出差分站RTK定位坐标；最后由基于扩展Jerk模型构造的Kalman滤波器实时修正差分站RTK定位坐标。

图2所示的仿真环境中SPIRENT GSS9000设备对应图1中的卫导模拟器；两台NovAtel FlexPak6型GNSS接收机中分别配置成基站与差分站，通过射频信号线(图2中实线连线)与SPIRENT GSS9000卫导模拟器射频信号输出端相连；基站与差分站输出的卫导观测量分别由RS-232串口线(图2中虚线连线)输出到计算机；计算机上运行卫星导航差分RTK定位程序，实时输出差分站RTK定位坐标。此外，基于本文所提算法所编写的Matlab程序也同时运行在该计算机上。

实验中，将基站位置设置成始终静止于地面某处，差分站的运动轨迹设置为在基站上空绕基站做匀速圆周机动，飞行高度为2 000 m，机动速度为100 m/s匀速，飞行半径为10 km。GNSS接收机每50 ms输出一次观测量，因此卫星导航差分RTK定位程序与本文算法的定位刷新率均为20 Hz。

基于上述相同的仿真设置，并且在每次仿真实验中差分站至少绕基站机动飞行1圈，独立进行100次仿真定位实验，差分站机动真实轨迹与卫星导航差分RTK定位软件以及经本文算法修正后给出的典型纬度、经度、高度轨迹如图3所示。

(a)纬度轨迹

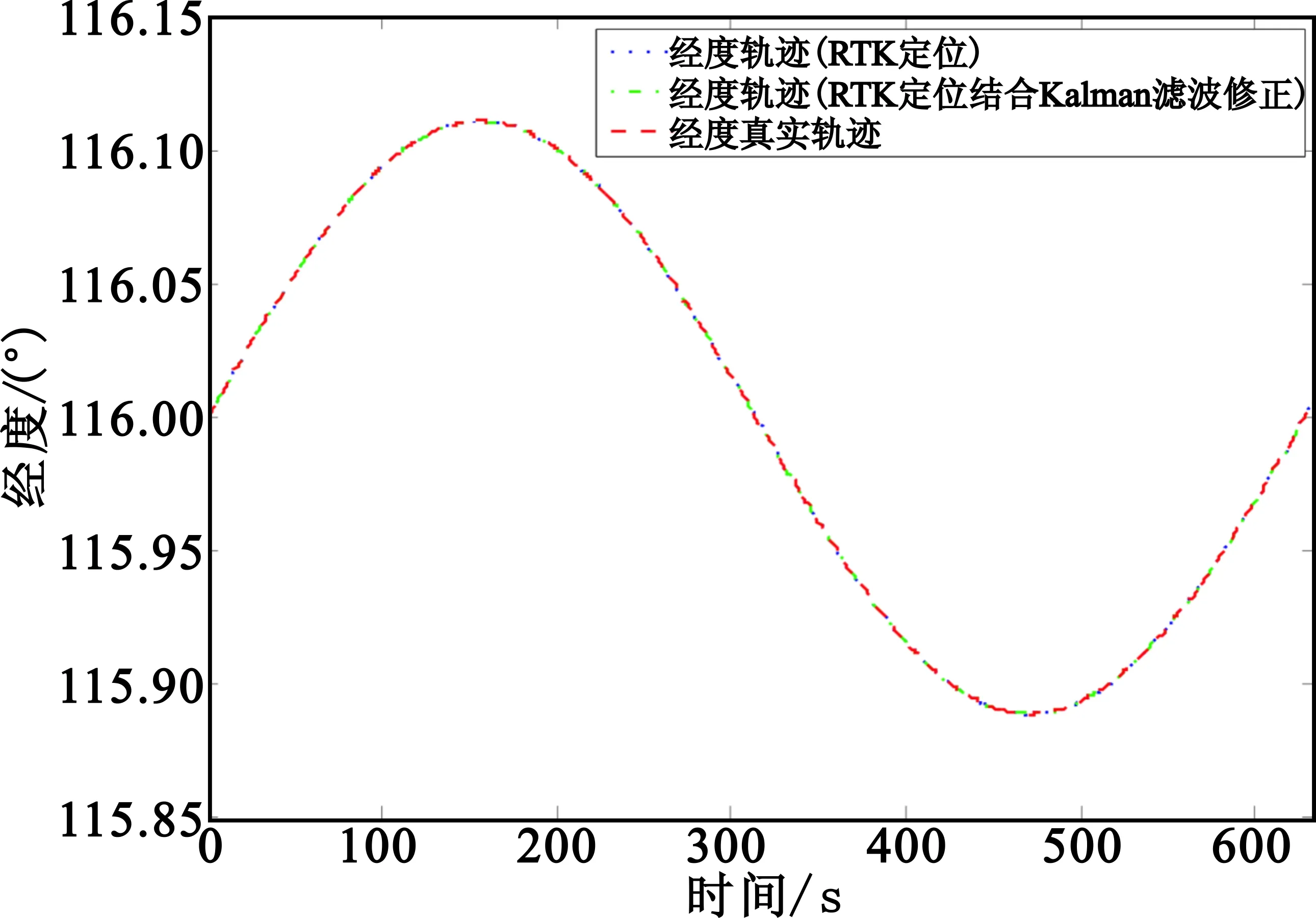
(b)经度轨迹

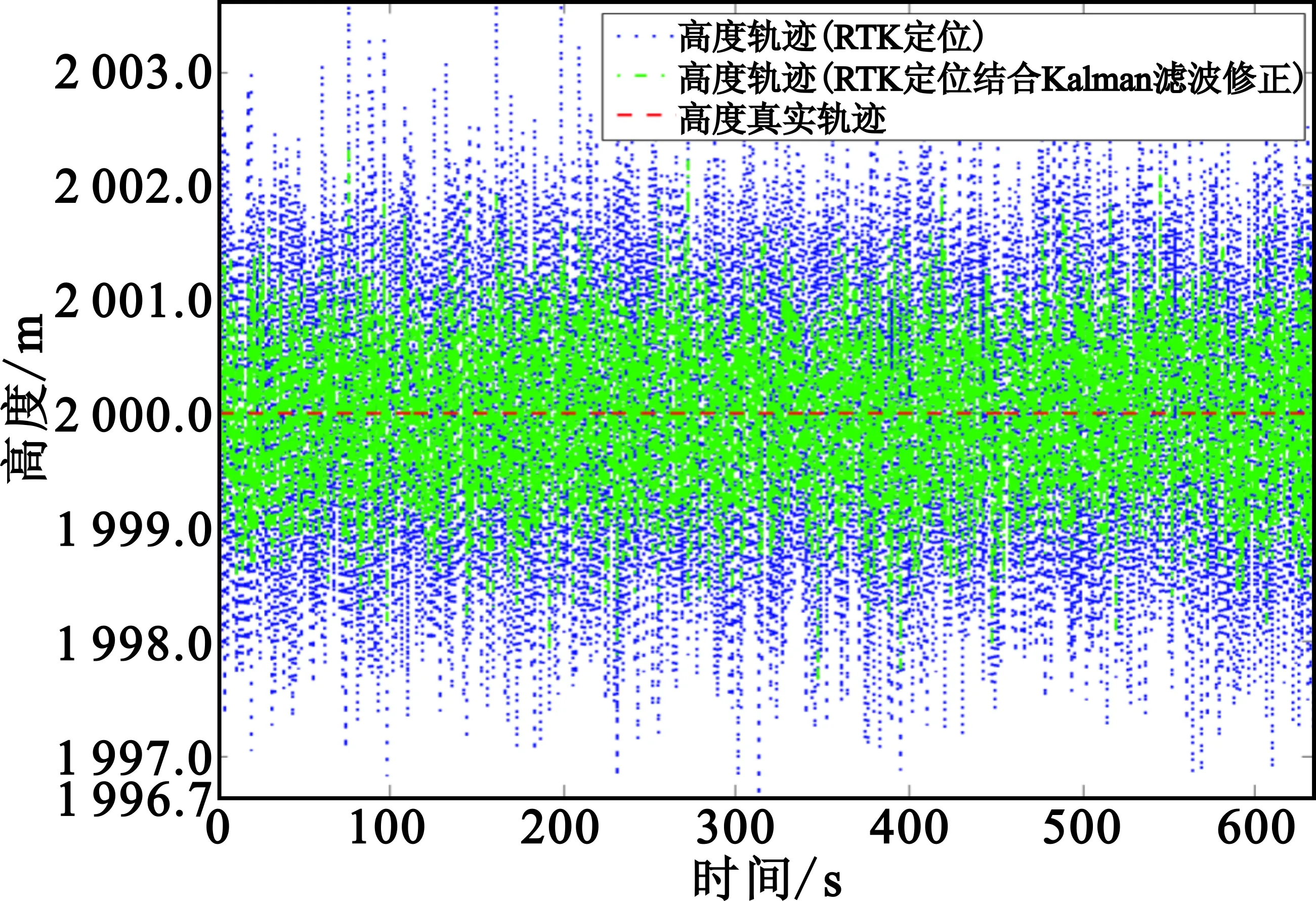
(c)高度轨迹

前文已分析到由于载波相位模糊度固定失败会造成卫星导航差分RTK定位坐标有时会出现大幅偏差，而这种偏差能从典型定位轨迹图中直观反映出。图3(c)显示RTK定位高度偏差幅度约为4 m，而Kalman滤波修正后高度偏离降至约2 m，这表明RTK定位给出的高度值相比Kalman滤波修正高度更偏离真实高度。为说明RTK定位在纬度与经度上的定位偏差，将图3(a)与(b)做局部放大显示，如图4所示。图4表明RTK定位在纬度上的定位偏差幅度达到(2×10-5)°(约2 m)，在经度上的定位偏差幅度也有(2×10-6)°(约0.2 m)，而经过Kalman滤波修正后纬度与经度(图中蓝色线条)更靠近真实轨迹(图中红色线条)。这些实验结果表明本文所提的卫星导航差分RTK定位坐标Kalman滤波修正算法能有效减小定位误差，提高定位精度。

(a)纬度局部放大图

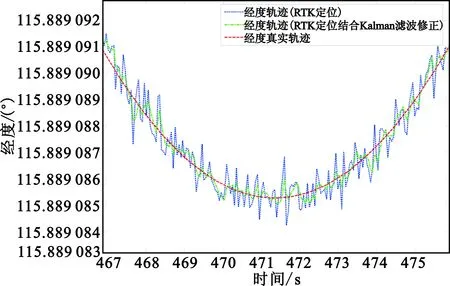
(b)经度局部放大图

定义如下估计误差均方根误差(Root Mean Squared Error,RMSE)指标：

(18)

式中：n表示独立实验次数，ζreal,i表示第i次实验的真值，ζobs,i表示第i次实验的观测值。那么，卫星导航差分RTK定位算法的定位误差纬度、经度、高度RMSE曲线和本文所提算法的定位误差纬度、经度、高度RMSE曲线如图5所示。

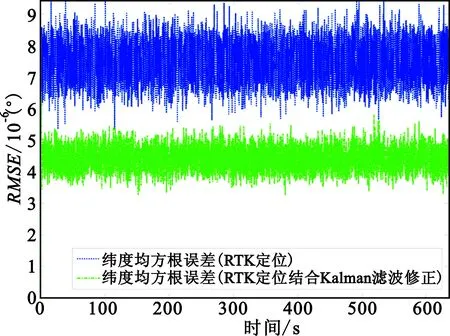
(a)纬度误差RMSE曲线

(c)高度误差RMSE曲线

从图5所示定位误差纬度、经度、高度RMSE曲线可以看出，经本文算法修正后的定位误差要明显小于卫星导航差分RTK定位算法的定位误差。经Kalman滤波修正后纬度误差RMSE指标由约(8×10-6)°(约0.8 m)降低到约(4×10-6)°(约0.4 m)，经度误差RMSE指标由约(1×10-6)°(约1 m)降低至约(6×10-6)°(约0.6 m)，高度误差RMSE指标从1 m附近减小到约0.6 m。可以证明，本文所提的卫星导航差分RTK定位坐标Kalman滤波修正算法能有效提高RTK定位精度，有利于提高系统的可靠性。

4 结 论

本文在分析卫星导航差分RTK定位技术出现定位偏差的原因的基础上，改进了Jerk模型。将卫星导航系统输出的载体速度信息引入Jerk模型，增广描述载体运行动态行为的状态空间模型。基于增广状态空间模型，利用Kalman滤波器实时修正卫星导航差分RTK定位坐标。半实物仿真实验结果表明，所提算法能显著降低RTK定位误差，提高工程应用场合卫星导航系统的可靠性。

[1] 楚瑞. EKF/UKF在编队飞行卫星GPS相对导航中的应用[J].空间控制技术与应用,2008,34(5): 57-60. CHU Rui. Application of EKF/UKF in the GPS relative navigation for formation flying of spacecrafts[J].Aerospace Control and Application,2008,34(5): 57-60.(in Chinese)

[2] 花江. 基于差分GPS的战术数据链高精度时间同[J].电讯技术,2016,56(4) : 389-393. HUA Jiang．High-precision time synchronization for collaborative tactical data link via differential GPS[J].Telecommunication Engineering,2016,56(4): 389-393.(in Chinese)

[3] 颜琳. 北斗/GPS双模CORS网研制与测试技术研究[D].上海: 上海交通大学,2013. YAN Lin. Development and testing technology research on Beidou/GPS integrated CORS network[D].Shanghai:Shanghai Jiaotong University,2013.(in Chinese)

[4] 何存见,李云涛,武伟,等. 遥感影像结合RTK绘制中大比例尺地形图的应用研究[J].测绘与空间地理信息,2011,34(1):132-135. HE Cunjian,LI Yuntao,WU Wei,et al.Research on application of medium and large scale topographic map in the technique of remote sensing images combined with RTK[J].Geomatics and Spatial Information Technology,2011,34(1):132-135.(in Chinese)

[5] CHEN D,LACHAPELLE G.A comparison of the FASF and least-squares search algorithms for on-the-fly ambiguity resolution[J].Journal of the Institute of Navigation,1995,42(2):371-390.

[6] MOHAMED A H,SCHWARZ K P. A simple and economical algorithm for GPS ambiguity resolution on the fly using a Whitening filter[J].Journal of the Institute of Navigation,1998,45(3):221-231.

[7] TEUNISSEN P J G. Least squares estimation of the integer GPS ambiguities[C]//Proceedings of General Meetings of the International Association of Geodesy(IAG).Beijing:IAG,1993:1-16.

[8] TEUNISSEN P J G. The least-squares ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation[J].Journal of Geodesy,1995,70(1):65-82.

[9] 陈树新,王永生. GPS整周模糊度估计的成功概率研究[J].弹箭与制导学报,2002,22(1):23-27. CHEN Shuxin,WANG Yongsheng. Study on success probability of integer GPS ambiguity resolution estimating[J].Journal of Projectiles,Rockets,Missiles and Guidance,2002,22(1):23-27.(in Chinese)

[10] TEUNISSEN P J G. Success probability of integer GPS ambiguity rounding and bootstrapping[J].Journal of Geodesy,1998,72(10):606-612.

[11] VERHAGEN S,LI B F,TEUNISSEN P J G. Ps-LAMBDA: ambiguity success rate evaluation software for interferometric applications[J].Computers & Geosciences,2013,54(4)：361-376.

[12] KISHORE M,PRAVAS R M. A Jerk model for tracking highly maneuvering targets[J].IEEE Transactions on Aerospace and Electronics Systems,1997,33(4):1094-1105.

[13] 何友,修建娟,关欣,等. 雷达数据处理及应用[M]．3版.北京: 电子工业出版社,2013.

[14] 谢钢. GPS 原理与接收机设计[M].北京: 电子工业出版社,2009.

Adjusting Differential GNSS RTK PositioningCoordinate via Kalman Filtering

XIONG Jie,AN Yi,KANG Ronglei,LI Yang,YANG Shaoshuai,ZUO Zhiyong

(Southwest China Institute of Electronic Technology,Chengdu 610036,China)

The positioning accuracy of the differential global navigation satellite system(DGNSS) real time kinematic(RTK) system is extremely influenced by the carrier phase integer ambiguity resolution algorithms. Especially,when the integer ambiguity is failed to be fixed,the positioning deviation is bound to sharply increase. Against this issue,based on the Jerk model,a DGNSS RTK positioning coordinate adjusting algorithm via the Kalman filtering is proposed in this paper. The traditional Jerk model is augmented by adding the velocity information obtained from the GNSS single-point positioning into the observation equations. Based on this augmented state space model,the Kalman filtering is used to real-time adjust the DGNSS RTK positioning coordinate. The hardware-in-the-loop simulation results show that the suggested adjusting algorithm can significantly improve the positioning accuracy of the DGNSS RTK system.

global navigation satellite system(GNSS);real time kinematic(RTK) technology;Jerk model;Kalman filtering

10.3969/j.issn.1001-893x.2017.06.009

熊杰，安毅，康荣雷，等.利用Kalman滤波修正卫星导航差分RTK定位坐标[J].电讯技术，2017,57(6):666-671.[XIONG Jie,AN Yi,KANG Ronglei,et al.Adjusting differential GNSS RTK positioning coordinate via Kalman filtering[J].Telecommunication Engineering,2017,57(6):666-671.]

2016-12-14；

2017-04-11 Received date:2016-12-14；Revised date：2017-04-11

TN961

A

1001-893X(2017)06-0666-06

熊 杰(1984—)，男，四川邛崃人，2014年获博士学位，现为工程师，主要研究方向为导航与自适应滤波等；

Email: xiongji_1209@163.com

安 毅(1983—)，男，云南楚雄人，2015年获博士学位，现为工程师，主要从事导航、信号处理等技术研究；

Email: mranyi@163.com

康荣雷(1984—)，男，山东德州人，2009年获硕士学位，现为工程师，主要研究方向为数据链网络定位、卡尔曼滤波算法等；

Email:kangronglei@163.com

李 阳(1987—)，男，四川遂宁人，2014年获博士学位，现为工程师，主要研究方向为阵列信号处理、多线性代数等；

Email: yangleecool@qq.com

杨少帅(1988—)，男，河北邢台人，2013年获硕士学位，现为工程师，主要研究方向为组合导航；

Email:juipop@163.com

左芝勇(1985—)，男，四川绵阳人，2015年获博士学位，现为工程师，主要研究方向为图像处理、视觉导航等。

Email:zzy.iprai@gmail.com

**通信作者：xiongji_1209@163.com Corresponding author：xiongji_1209@163.com，安 毅，康荣雷，李 阳，杨少帅，左芝勇