改进高阶Vanderpol振子在微弱信号检测中的应用*

姜 烁，徐艳春

(梯级水电站运行与控制湖北省重点实验室(三峡大学)，湖北 宜昌 443002)



改进高阶Vanderpol振子在微弱信号检测中的应用*

姜 烁，徐艳春**

(梯级水电站运行与控制湖北省重点实验室(三峡大学)，湖北 宜昌 443002)

在高精度的微弱光电信号检测系统中，存在信号被强噪声湮没的情况。针对这一问题，提出了一种基于改进高阶Vanderpol振子的微弱正弦信号定量检测方法。该方法利用改进高阶广义Vanderpol系统的高灵敏度与强抗噪性的特点提高了微弱信号检测的可靠性，再结合Lyapunov指数定量检测和90°移相补偿来实现混沌系统状态的量化判断和待测信号参数的高精度提取。仿真结果表明改进的Vanderpol振子比传统Vanderpol振子运算速度更快。与传统Duffing振子相比，在5%幅值检测误差范围内，改进的高阶广义Vanderpol系统可多获得37 dB的信噪比增益和60 dB的检测门限增益；与基于相轨迹突变定性检测待测信号幅相法相比，90°移相补偿幅相定量检测法在信噪比降低时其检测相对误差仍可控制在2%以内。改进算法实现了微弱正弦信号的高灵敏度和高精度的幅相检测。

电力系统；微弱信号检测；混沌系统；Vanderpol振子；移相补偿；Lyapunov指数

1 引 言

在电力系统中，常涉及到微弱光电信号的检测问题，如电力设备早期产生的故障微弱信号检出、电力系统绝缘检测等，检测精度关系到电力系统的安全和经济运行。在高精度的微弱光电信号检测系统中，为了减小零点漂移对恒定微弱光电信号的影响，首先通过调制盘将光电信号调制成周期信号，在温度、压力等外界因素的影响下，会在传感器上接收到含噪声的微弱正弦周期信号。采用传统的检测方法提取信号参数，不能满足现有的检测精度要求，此时亟需一种将微弱周期信号从强噪声中提取出来的新方法[1-3]。

在现研究阶段，通过混沌理论去提取强噪声下的微弱信号参数的方法优于传统检测方法，并且其具有硬件易实现、成本低的优势，故有广阔的应用前景。文献[2]实现了基于Duffing混沌振子高精度估计微弱信号相位参量的方法；文献[3]利用多混沌振子阵列实现信号在不同初始相位的检测；文献[4]将互相关与混沌理论相结合，进一步增强传统方法微弱信号频域检测能力。但现有通过混沌检测微弱信号的理论方法也存在以下限制：一是对一阶非线性系统讨论较多，其中大多数以Duffing方程模型为代表，而对利用高阶混沌系统如Vanderpol系统等检测强噪声背景下微弱信号参量问题研究很少，并且Duffing系统在低信噪比时存在检测灵敏度不足的问题；二是研究者多采用基于相轨迹突变定性检测待测信号幅相的方法，使得检测缺乏定量判断依据，无法满足电力系统中微弱信号的检测精度要求，局限了其应用范围[2-5]。

针对以上的不足，本文提出了一种针对电力系统微弱周期信号检测的新算法。该算法拟在改进的高阶广义Vanderpol振子基础上，将提出的90°移相补偿与Lyapunov指数定量检测相结合，实现混沌系统状态的量化判断和待测信号参数的高精度提取。针对这一算法，文中详细介绍了其检测原理及实现过程，并进行了仿真验证。

2 高阶广义Vanderpol振子的改进

2.1 系统数学模型改进

广义Vanderpol振子是一个具有强非线性阻尼项的微分方程[6]，其方程的标准形式为

(1)

当δ、α确定后，振子系统存在唯一的奇点(0，0)和稳定的极限环。而周期信号检测模型的关键在于，系统方程存在一个有界的稳定解，即在非线性动力学范畴内，具有一个稳定的极限环存在,故广义Vanderpol振子可以用于微弱谐波信号检测。

当i=3时，标准方程的恢复力项为α1x+α2x3+α3x5(αi>0)。仿真测试中发现，此时系统的复杂度过高，不具有良好的运算速度，但系统对噪声有更强的免疫性。从降低系统的复杂度、保留系统对噪声的强免疫性几方面综合考虑，构造改进的高阶广义Vanderpol振子系统，并最终确定模型为

(2)

引入变量，则式(2)可转化为

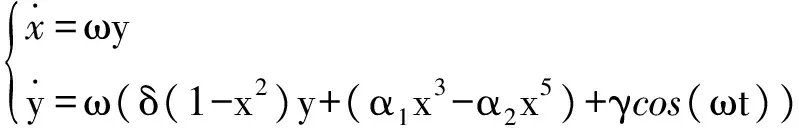
(3)

式中：ω为待测周期信号的频率，δ为阻尼比，γcos(ωt)为周期策动力，-α1x3+α2x5为改进高阶非线性恢复力项。

2.2 噪声对改进系统的影响分析

采用随机微分方程理论来分析噪声对改进高阶广义Vanderpol混沌振子的影响。在无噪声的情况下，令ω=1 rad/s，系统的微分方程为

(4)

在含噪声情况下，设式(4)的解为x(t)。Δx(t)为噪声对x(t)的微小扰动，n(t)为噪声,则系统的微分方程为

[α1(x+Δx)3-α2(x+Δx)5]=

γcos(t)+n(t)。

(5)

式(5)减去式(4)，并略去Δx(t)的二次及以上的项，可得

(6)

式(6)的矢量式为

(7)

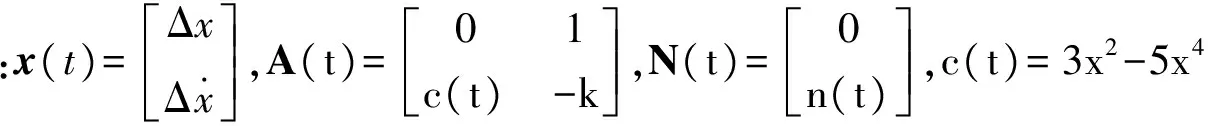
式(7)的解为

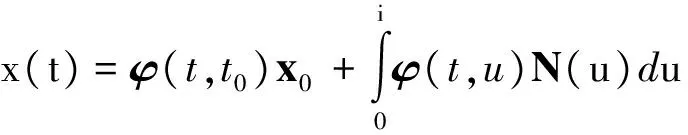
(8)

式中：φ是系统的状态转移矩阵。由于第一项是暂态解，会很快衰减到零，可以主要考虑系统稳态时的统计特性，故略去第一项，得到

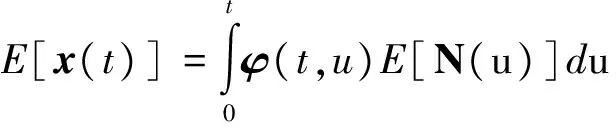
(9)

若E[N(u)]=0，则E[x(t)]=0。由此可知，统计意义下，任意分布的零均值噪声都不会使改进高阶广义Vanderpol混沌振子发生相轨迹变化。

3 微弱正弦信号的定量检测原理

利用混沌系统对同频率微弱周期信号的敏感性以及强抗噪性的特点，将待测微弱正弦信号加入混沌系统，然后根据系统状态是否发生由混沌状态到大周期状态的相态突变，检测同频微弱正弦信号是否存在及其参数(例如频率、幅值、相位等)。本文研究针对无频差情况下微弱正弦信号幅值和相位的定量检测。

3.1 基于Lyapunov指数的混沌状态定量判别

实现微弱周期信号的精确检测，前提是对系统混沌与周期状态进行准确的判定并得出精确的策动力值。与定性观察相轨迹图突变判定系统状态方法相比[7]，本文采用Lyapunov特征指数法[4]可定量度量在相空间中两条相轨迹随时间按指数率吸引或分离的程度，即定量判定相轨迹发散或收敛的比率并反映系统状态和精确的策动力值。

Lyapunov特征指数由下式定义：

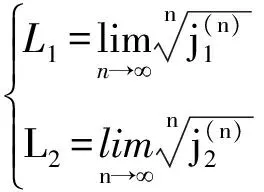
(10)

式中：L1和L2分别表示点变换时沿X方向与沿Y方向距离伸长或缩短倍数的平均值，其值大于0表示会伸长，小于0表示会缩短。若有L1>0、L2<0，系统在X方向伸长，在Y方向缩短，从而使系统局部不稳定，故有可能出现Smale马蹄映射，即混沌。在混沌的判据中，Lyapunov指数起着非常重要的作用。一个系统是否是混沌，可以由它的Lyapunov指数是否有正值来确定，这种定量确定方式比定性观察相图的方法更准确[8-13]。

系统混沌状态具体程序判别流程如图1所示。

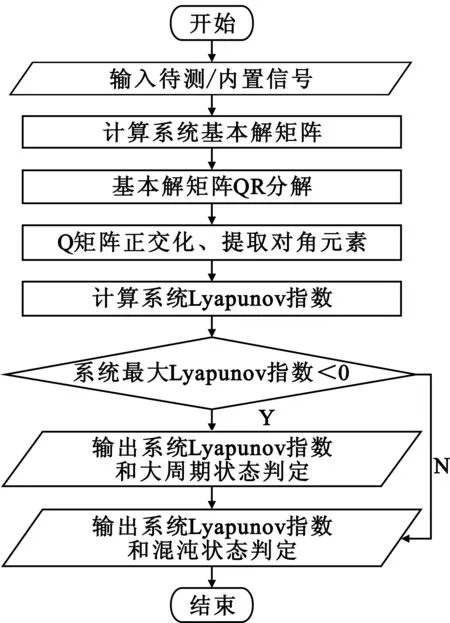
图1 系统混沌状态的判别流程图

3.2 90°移相补偿的幅相检测方法

当系统处于从混沌状态向大周期状态过渡的临界状态时，通过Lyapunov指数定量判定系统临界状态，得出策动力为γd。然后加入同频率待测微弱正弦信号acos(ωt+φ)，此时系统的总周期策动力变为

γ(t)=γdcos(ωt)+acos(ωt+φ)=γ′cos(ωt+θ)。

(11)

式中：

(12)

θ=arctg[asinφ/(γd+acosφ)]。

(13)

由于所测信号幅值微弱，即a<<γd,故由式(13)可知θ影响可忽略。

设定系统初始临界状态为混沌状态，当γ′>γd时，系统状态改变为大周期状态，此时待测信号被检测到，继续调节系统策动力γd，使系统状态刚好回到初始临界混沌状态，记录此时策动力γd′。由此可知

(14)

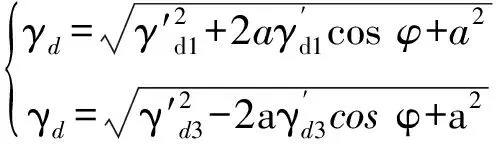
(15)

(16)

通过求解式(15)与式(16)，将得到的两组相位φ1、φ2和幅值a1、a2分别取平均值，得出最终的待测信号幅值相位φ和幅值a。系统90°移相补偿幅相的检测具体流程如图2所示。

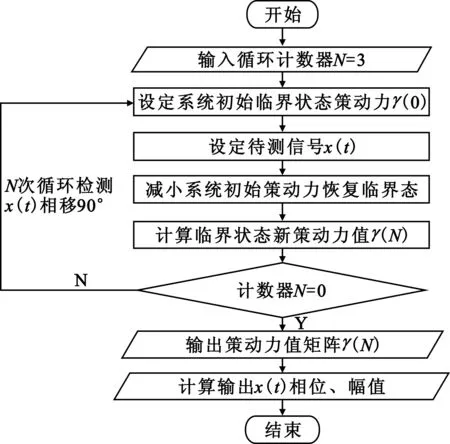
图2 系统90°移相补偿的幅相检测流程图

90°移相补偿的原理为：通过对待测信号分别进行90°移相，构造两组具有互补相变特性的检测状态(例如移相0时，检测状态为混沌状态过渡到大周期状态，与之同组移相π时，其检测状态为大周期状态过渡到混沌状态)。通过互补相变特性检测待测信号，可抵消部分由噪声带来的偏差；通过对两组相位φ1、φ2和幅值a1、a2分别取平均值，可以消除随机因素带来的误差,故90°移相补偿幅相检测可以提高检测精度。

4 仿真实验分析

4.1 改进的高阶Vanderpol振子性能测试

为验证本文改进的高阶Vanderpol振子具有检测微弱周期信号的优越性，构建模拟待测信号[5]，依据电力系统微弱光电信号实际存在的环境中噪声的主要成分，构建仿真试验的噪声环境。分别采用Duffing系统、传统高阶广义Vanderpol 系统和改进的高阶广义Vanderpol 系统对同一待测信号进行检测。其中，Duffing系统已被证明能有效检测微弱周期信号[10-11]。以下仿真实验均在Matlab-2012a环境下进行(处理器为内存4 GB、i3-3240@3.40 GHz)。

仿真实验1：检测门限相同时两种混沌系统噪声免疫力比较。基于前期测试，综合考虑计算时间及效果，取迭代次数N=104，步长h=0.01 s。设置待检微弱正弦信号幅值为A=10-8A，频率为ω=700π rad/s。在不同信噪比情况下，对其幅值大小进行检测，并对传统高阶广义Vanderpol 系统和改进高阶广义Vanderpol 系统运算时间取均值。仿真结果如表1和表2所示。

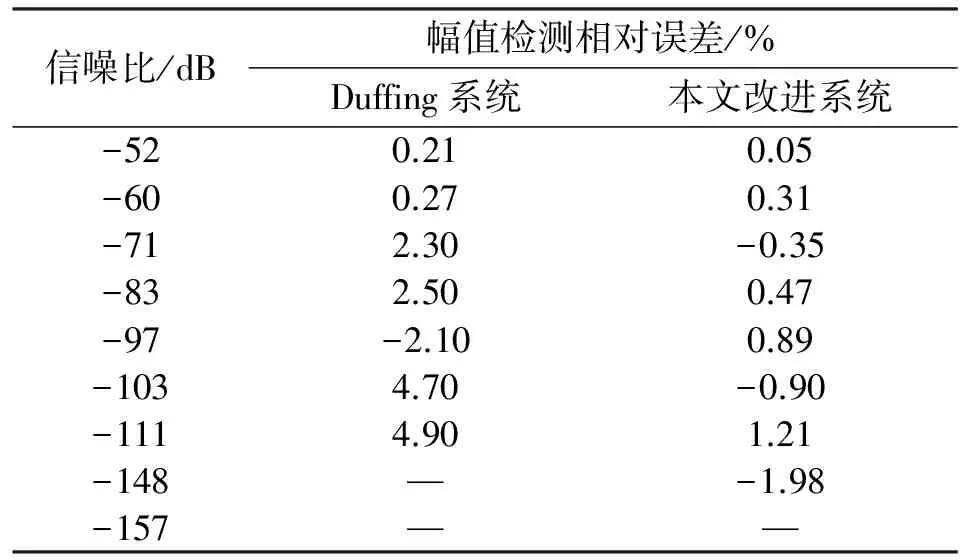
表1 相同检测门限两类系统检测结果对比表Tab.1 Comparison of detection result between two kindsof oscillator with the same detection threshold

表2 相同检测门限两类系统运算时间对比表Tab.2 Comparison of operation time between two kinds of oscillator with the same detection threshold

仿真实验2：噪声方差相同时两种混沌系统检测灵敏度比较。取迭代次数N=104，步长h=0.01 s。设置高斯白噪声的噪声方差为0.03，待检微弱正弦信号频率为ω=700π rad/s。对幅值大小不同的待测信号进行检测，并对传统高阶广义Vanderpol 系统和改进高阶广义Vanderpol 系统运算时间取均值。仿真结果如表3和表4所示。

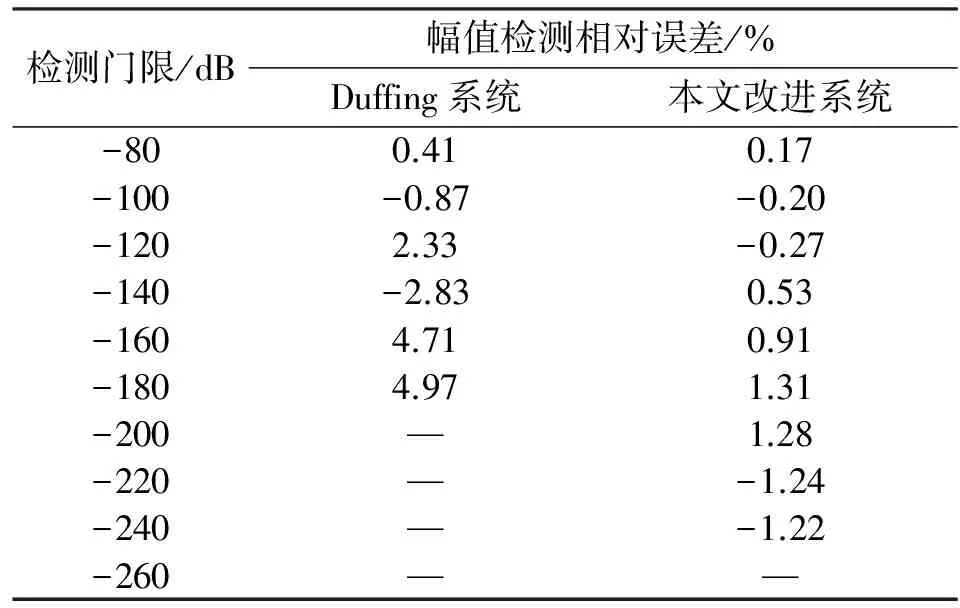
表3 相同噪声方差两类系统检测结果对比表Tab.3 Comparison of the detection result between two kinds of oscillator with the same noise variance

表4 相同噪声方差两类系统运算时间对比表Tab.4 Comparison of operation time between two kinds of oscillator with the same noise variance

从仿真实验1、2的结果可知,在幅值检测相对误差小于5% 条件下[14]，当检测门限相同时，本文改进的高阶广义Vanderpol系统的信噪比可达-148 dB，与Duffing系统相比，可获得37 dB的信噪比增益。当噪声方差相同时，本文改进的高阶广义Vanderpol系统的最低检测门限可达-240 dB，与Duffing系统相比，可获得60 dB的增益，大幅提高了信号检测灵敏度。同时，与传统高阶广义Vanderpol 系统相比，改进的高阶广义Vanderpol系统的运算时间明显缩短。故本文改进的高阶广义Vanderpol系统降低系统的复杂度，具有良好的运算速度和检测精确度，对噪声也有强免疫性。

4.2 基于Lyapunov指数定量检测仿真分析

为验证本文提出的基于Lyapunov指数定量检测微弱正弦信号幅相方法的有效性，对同一混有高斯白噪声的待测信号，分别采用基于相轨迹突变定性检测待测信号幅相法和本文方法进行仿真实验。

文献[5]中介绍的基于相轨迹突变定性检测待测信号幅相法，是经过验证的有效检测方法。其基本原理是观察混沌系统相轨迹的瞬态突变特征来确定混沌系统的状态并估计策动力值，通过将系统策动力相位反相，获得一组具有互补相变特性的检测状态,再利用估计策动力，求得待测信号幅相。

仿真实验3：使用3.1节提出的方法对改进高阶Vanderpol系统临界状态判别并得出策动力值。利用相轨迹图初步确定了广义Vanderpol混沌振子系统临界时，初始策动力阈值为γ=0.346 499 78。令策动力迭代步长为Δγ=10-12。计算每个γ值对应的Lyapunov特性指数，如果连续有10个最大Lyapunov特性指数小于零，则跳出循环。此时γ值减10-11，即为所求的策动力阈值γd。仿真结果如表5和图3所示。

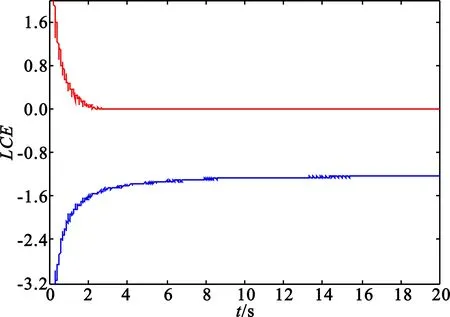
图3 系统临界态Lyapunov特性指数图

由表5可知，仿真初始时系统最大Lyapunov特性指数大于零，说明系统处于混沌状态。

从γ=0.346 499 784 894开始，连续10次循环所对应的系统最大Lyapunov特性指数都小于零，说明系统己经完全过渡到了周期态，则式(3)的临界状态阈值γ=0.346 499 784 893。观察此时x(t)的时间历程曲线(见图4)，也可验证该阈值的准确性。

(a)γ=0.346 499 784 893时混沌态系统

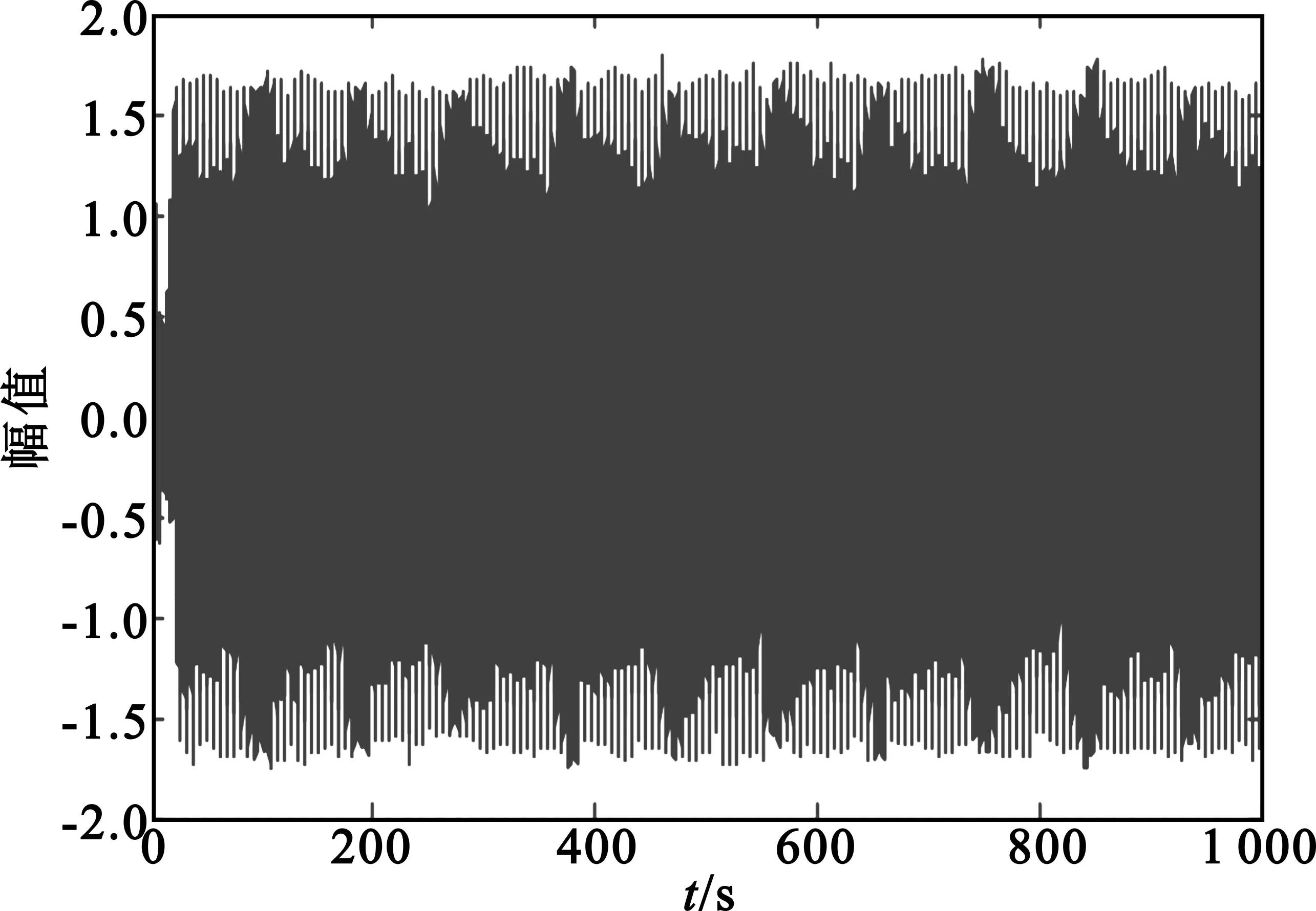
(b)γ=0.346 499 784 894时周期态系统

同时由表5中可观察到γ=0.346 499 784 891时，系统的最大Lyapunov特性指数小于零，但此时为系统不稳定状态，如通过相轨迹图判定混沌阈值，则会出现误判。参考γ=0.346 499 784 890与γ=0.346 499 784 891时的相轨迹图(见图5)，可看到系统发生了瞬态同步突变，但此时γ=0.346 499 784 890值并不是混沌系统阈值。采用最大Lyapunov特性指数进行多次判定即可避免误判。

(a)γ=0.346 499 784 890

(b)γ=0.346 499 784 891

仿真实验4：对基于相轨迹突变定性检测待测信号幅相法(简称定性检测)和本文方法进行检测有效性对比。在Matlab-2012a环境下，依式(3)构建改进的高阶广义Vanderpol系统。令δ=0.5，设待测信号为

x(t)=acos(ωt+φ)+n(t)。

式中：a=0.000 1 A，ω=700π，φ=0.24π，n(t)为高斯白噪声幅值。在不同信噪比下进行仿真检测，仿真结果如图6所示。从图6可知，采用本文方法进行幅相检测可将相对误差控制在2%以内，而定性检测方法的检测误差远超2%并有随信噪比降低相对误差增加的趋势。从检测结果可知使用Lyapunov指数可定量判断系统状态，为后续幅相检测提供精确临界策动力值；同时采用90°移相补偿幅相检测，通过构造两组互补相变特性检测待测信号，可抵消部分由噪声带来的偏差，对结果取平均值，可以消除随机因素带来的误差,故使得本文方法具有更高检测精度。存在误差的原因是,受仿真时间限制，使得迭代次数有限，导致策动力值的精度受限。可以通过优化系统参数和增加迭代次数，提高待测信号幅相值的计算精度。

(a)幅值检测相对误差

(b)相角检测相对误差

5 结 论

本文提出了一种针对电力系统微弱周期信号检测的新算法，在改进的高阶广义Vanderpol系统基础上引入了90°移相补偿和Lyapunov指数来实现待测信号的定量检测。仿真实验对比结果显示，在幅值检测相对误差小于5% 条件下，与传统高阶广义Vanderpol 系统相比，改进的Vanderpol系统具有良好的运算速度；和Duffing系统相比，改进的高阶广义Vanderpol系统具有更高的检测精度和抗噪免疫力；和基于相轨迹突变定性检测待测信号幅相法相比，本文改进方法在信噪比降低时其相对误差仍可控制在2%以内，使其具有更高检测精度，证明了该方法的有效性，其在理论上是可行的。

[1] 李岩松,欧阳进,刘君,等. 基于Allan方差的磁光玻璃型光学电流互感器噪声分析[J].电力系统自动化,2015,39(12):126-129. LI Yansong,OUYANG Jin,LIU Jun,et al.Analysis on noise of magneto-optical glass type optical current transformer based on Allan variance[J].Automation of Electric Power Systems,2015,39(12):126-129.(in Chinese)

[2] 孙文军,芮国胜,王林,等. 一种利用Duffing-Vanderpol振子估计弱信号相位的方法[J].电讯技术,2016,56(1):14-19. SUN Wenjun,RUI Guosheng,WANG Lin,et al.Estimation of weak signal phase by using Duffing-Vanderpol oscillator[J].Telecommunication Engineering,2016,56(1):14-19.(in Chinese)

[3] COELHO L S,GUERRA F A,BATISTELA N J,et al.Multi-objective cuckoo search algorithm based on Duffing′s oscillator applied to Jiles-Atherton vector hysteresis parameters estimation[J].IEEE Transactions on Magnetics,2013,49(5):1745-1748.

[4] 陈伟根,云玉新,杜林,等. 基于互相关和李雅普诺夫指数的微弱正弦信号混沌检测[J].电力系统自动化,2008,32(18):44-48. CHEN Weigen,YUN Yuxin,DU Lin,et al.Chaotic detection of weak sine signals based on cross-correlation and Lyapunov exponent[J].Automation of Electric Power Systems,2008,32(18):44-48.(in Chinese)

[5] 罗志坤,曾喆昭. 基于扩展型 Duffing 振子的高精度测频方法[J].电力系统自动化,2015(16):81-85. LUO Zhikun,ZENG Zhezhao. A highly accurate frequency-measuring method based on extended Duffing oscillator[J].Automation of Electric Power Systems,2015(16):81-85.(in Chinese)

[6] 王震,孙卫,蔺小林. 多自由度Vanderpol振子极限环计算[J].计算机工程与应用,2012,48(13):230-233. WANG Zhen,SUN Wei,LIN Xiaolin. Computing for limit cycle of Vanderpol oscillator with multi degree of freedom[J].Computer Engineering and Applications,2012,48(13):230-233.(in Chinese)

[7] 徐一红,祝长生,赵耀培,等. 基于稀疏分解和混沌理论的微弱信号检测[J].电讯技术,2015,55(11):1194-1199. XU Yihong,ZHU Changsheng,ZHAO Yaopei,et al.Weak signal detection based on sparse decomposition and chaotic theory[J].Telecommunication Engineering,2015,55(11):1194-1199.(in Chinese)

[8] 鲍枫,刘鑫,贾懋珅,等. 音频信号的混沌特性分析[J].电讯技术,2011,51(7):97-102.

BAO Feng,LIU Xin,JIA Maoshen,et al.Chaotic characteristic analysis of audio signals[J].Telecommunication Engineering,2011,51(7):97-102.(in Chinese)

[9] XU Yanchun,YANG Chunling,ZHAI Xiaodong. A new approach to detecting weak signal in strong noise based on chaos system control[J].Chinese Physics B,2010,19(3):202-206.

[10] 石盛超,李广侠,李志强,等. 基于欠采样随机共振的单频微弱信号检测新方法[J].电讯技术,2014,54(5):605-610. SHI Shengchao,LI Guangxia,LI Zhiqiang,et al.A novel weak single frequency signal detection method based on under sampling stochastic resonance[J].Telecommunication Engineering,2014,54(5):605-610.(in Chinese)

[11] GAO X H,LIU X W,SHAO S Q.Projective synchronization in coupled fractional order chaotic rossler system and its control[J].Chinese Physics B,2007,16(9):2612-2615.

[12] PLATAS-GARZA M A,SERNA J A.Polynomial implementation of the Taylor-Fourier transform for harmonic analysis[J].IEEE Transactions on Instrumentation and Measurement,2014,63(12):2846-2854．

[13] WANG H W,ZHAO G Q. Improved Rife algorithm for frequency estimation of sinusoid wave[J].Signal Processing,2010(26):1573-1576.

[14] 电能质量电力系统频率偏差:GB/T 15945—2008[S].北京:中国电力出版社,2008.

Application of Improved Higher Order Vanderpol Oscillatorin Weak Signal Detection

JIANG Shuo,XU Yanchun,LIU Yulong,DU Yufei

(Hubei Key Laboratory of Cascaded Hydropower Stations Operation &Control(China Three Gorges University),Yichang 443002,China)

The signal will be submerged by strong noise in the high precision weak photoelectric signal detection system. A novel approach for quantitative detection of weak sine signal based on Vanderpol oscillator is proposed to solve this problem. The new method improves the reliability of weak signal detection by refining the high order generalized Vanderpol oscillator with higher sensitivity and stronger noise immunity. At the same time,quantitative judgment of the state of chaotic system is achieved with Lyapunov index and higher precision extraction of the signal parameters is realized by combining Lyapunov index with 90 degrees phase shift compensation. Simulation result shows that the improved Vanderpol oscillator has faster computing speed than the traditional one. The improved Vanderpol oscillator can obtain 37 dB signal-to-noise ratio(SNR) gain and 60 dB detection threshold gain compared with the traditional Duffing oscillator in the range of 5% amplitude detection error. The detection based on 90° phase shift compensation can control the relative error within 2% compared with the amplitude and phase detection based on phase trajectory mutation when the SNR is reduced. Therefore the high sensitive and precise detection of weak signal's amplitude and phase is realized.

power system;weak signal detection;chaotic system;Vanderpol oscillator;phase shift compensation;Lyapunov index

2016-11-01；

2017-01-16 Received date:2016-11-01；Revised date：2017-01-16

教育部留学回国人员科研启动基金(KJ2015QT007)

10.3969/j.issn.1001-893x.2017.06.011

姜烁，徐艳春，刘宇龙，等.改进高阶Vanderpol振子在微弱信号检测中的应用[J].电讯技术，2017,57(6):678-684.[JIANG Shuo,XU Yanchun,LIU Yulong,et al.Application of improved higher order Vanderpol oscillator in weak signal detection[J].Telecommunication Engineering,2017,57(6):678-684.]

TN911.23

A

1001-893X(2017)06-0678-07

姜 烁(1993—)，女，黑龙江铁力人，2016年于三峡大学获学士学位，现为华北电力大学硕士研究生;

徐艳春(1973—)，女，黑龙江哈尔滨人，2010年于哈尔滨工业大学获博士学位，现为三峡大学电气与新能源学院副教授、硕士生导师，主要研究方向为矩阵变换器在电力系统中的应用、电力系统继电保护中的电气信号检测技术;

Email:xyc7309@163.com

刘宇龙(1991—)，男，湖北宜昌人，硕士研究生，主要研究方向为电网的谐波检测及微弱电气信号检测;

杜于飞(1994—)，男，湖北宜昌人，硕士研究生，主要研究方向为电网的谐波检测及微弱电气信号检测。

**通信作者：xyc7309@163.com Corresponding author：xyc7309@163.com，刘宇龙，杜于飞