三角形的认识与证明

姚万里

一、选择题

1. 下列每组数分别是三根木棒的长度，能用它们摆成三角形的是（ ）

A.3 cm、4 cm、8 cm

B.8 cm、7 cm、15 cm

C.5 cm、5 cm、11 cm

D.13 cm、12 cm、20 cm

2.到三角形的三个顶点的距离都相等的点是这个三角形的（ ）

A.三条高的交点

B.三条角平分线的交点

C.三条中线的交点

D.三条边的垂直平分线的交点

3.一个等腰三角形的两边长分别为4，8，则它的周长为（ ）

A.12 B.16

C.20 D.16或20

4.如图1，直线m∥n，∠1=70°，∠2=30°，则∠A等于（ ）

A.30° B.35°

C.40° D.50° [A][B][C][D][m][n][1][2][3] [E][A][B][C][D][图1 图2]

5.如图2，AD是∠EAC的平分线，AD∥BC，∠B=30°，则∠C的度数为（ ）

A.50° B.40°

C.30° D.20°

6.如图3，线段AC的垂直平分线交线段AB于点D，∠A=50°，则∠BDC=（ ）

A.50° B.100°

C.120° D.130° [A][B][C][D][E][A][B][C][D][图3 图4]

7.如图4，在△ABC中，AB=AC，AD是∠BAC的平分线.已知AB=5，AD=3，则BC的长为（ ）

A.5 B.6

C.8 D.10

8.如图5，在△ABC中，∠ACB=90°，AC=8，AB=10，DE垂直平分AC交AB于点E，则DE的长为（ ）

A.6 B.5

C.4 D.3 [A][B][C][D][E][A][B][C][D][O] [图5 图6]

9.将一副三角板如图6放置，若∠AOD=20°，则∠BOC的大小为（ ）

A.140° B.160°

C.170° D.150°

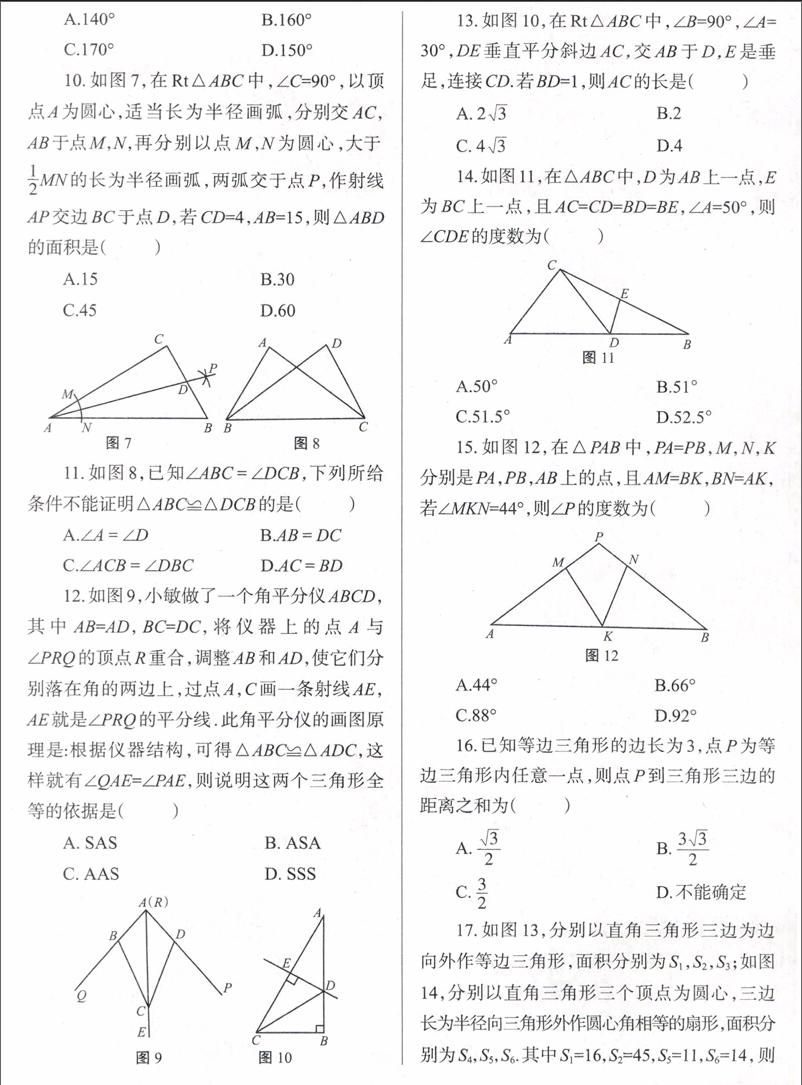
10.如图7，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M，N，再分别以点M，N为圆心，大于

[12]MN的长为半径画弧，两弧交于点P，作射线AP交边BC于点D，若CD=4，AB=15，则△ABD的面积是（ ）

A.15 B.30

C.45 D.60 [A][B][C][D] [A][B][C][D][M][N][P][图7 图8]

11.如图8，已知∠ABC=∠DCB，下列所给条件不能证明△ABC≌△DCB的是（ ）

A.∠A=∠D B.AB=DC

C.∠ACB=∠DBC D.AC=BD

12.如图9，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线.此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE，则说明这两个三角形全等的依据是（ ）

A. SAS B. ASA

C. AAS D. SSS [图9 图10][A（R）][B][C][D][E][A][B][C][D][E][P][Q]

13.如图10，在Rt△ABC中，∠B=90°，∠A=30°，DE垂直平分斜边AC，交AB于D，E是垂足，连接CD.若BD=1，则AC的长是（ ）

A.[23] B.2

C.[43] D.4

14.如图11，在△ABC中，D为AB上一点，E为BC上一点，且AC=CD=BD=BE，∠A=50°，则∠CDE的度数为（ ） [A][B][C][D][E][图11]

A.50° B.51°

C.51.5° D.52.5°

15.如图12，在△PAB中，PA=PB，M，N，K分别是PA，PB，AB上的点，且AM=BK，BN=AK，若∠MKN=44°，则∠P的度数为（ ）[A][B][P][M][N][K][图12]

A.44° B.66°

C.88° D.92°

16.已知等边三角形的边长为3，点P为等边三角形内任意一点，则点P到三角形三边的距离之和为（ ）

A.[32] B.[332]

C.[32] D.不能确定

17.如图13，分别以直角三角形三边为边向外作等边三角形，面积分别为S1，S2，S3；如圖14，分别以直角三角形三个顶点为圆心，三边长为半径向三角形外作圆心角相等的扇形，面积分别为S4，S5，S6.其中S1=16，S2=45，S5=11，S6=14，则S3+S4=（ ）

A.86 B.64

C.54 D.48 [S1][S2][S3] [S4][S5][S6][图13 图14][A][B][C]

二、填空题

18.如图15，O为数轴的原点，A，B两点分别对应-3，3，作腰长为4的等腰△ABC，连接OC，以O为圆心，CO长为半径画弧交数轴的正半轴于点M，则点M对应的实数为 . [-3 -2 -1 O 1 2 3][A][B][C][M][A][B][C][D][F][E][图15 图16]

19.如图16，在△ABC中，AB=AC，BC=12 cm，点D在AC上，DC=4 cm，将线段DC沿CB方向平移7 cm得到线段EF，点E，F分别落在边AB，BC上，则△EBF的周长是 cm.

20.如图17，在3×3的方格中，A，B，C，D，E，F分别位于格点上，从C，D，E，F四点中任取一点，以点A，B为顶点作三角形，则所作三角形为等腰三角形的概率是 .[＼&＼&＼&＼&＼&＼&＼&＼&＼&] [A][B][C][E][D][F][A][B][C][D][E][F][·][·][·][·][·][·][图17 图18]

21.在△ABC中，若∠A=90°，则∠ABC的角平分线和∠ACB的角平分线所构成的角的度数为 .

22.如图18，在Rt△ABC中，∠ACB=90°，BC=6，AC=8，分别以点A，B为圆心，大于线段AB长度的一半为半径作弧，相交于点E，F，连接EF，交AB于点D，连接CD，则CD的长是 .

23.如图19，在四边形ABCD中，∠A=90°，AB=[33]，AD=3，点M，N分别为线段BC，AB上的动点（含端点，但点M不与点B重合），点E，F分别为DM，MN的中点，则EF长度的最大值为 . [A][B][C][D][E][F][M][N][A][B][C][D][E][O][图19 图20]

24.如图20，在△ABC中，分别以AC，BC为边作等边三角形ACD和等边三角形BCE，连接AE，BD交于点O，则∠AOB的度数为 .

25.有一个面积为[53]的等腰三角形，它的一个内角是30°，则以它的腰长为边的正方形的面积为 .

26.如图21，P是等边三角形ABC内一点，将线段AP绕点A顺时针旋转60°得到线段AQ，连接BQ.若PA=6，PB=8，PC=10，则四边形APBQ的面积为 . [A][B][C][D][E][F][B][C][P][Q][A][图21 图22] 27.如图22，等边△ABC的边长为4，AD是BC边上的中线，F是AD边上的动点，E是AC边上一点，若AE=2，当EF+CF取最小值时，∠ECF的度数为 .

28.如图23，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD是∠BAC的平分线.若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是 .[A][B][C][D][P][Q] [图23]

三、解答题

29.如图24，点D是AB上一点，DF交AC于点E，DE=FE，FC∥AB.

求证：AE=CE.

30.如图25，在△ABC中，D为AB的中点.

（1）请用尺规作图法作边AC的中点E，并连接DE（保留作图痕迹，不要求写作法）；

（2）在（1）的条件下，若DE=4，求BC的长. [A][B][C][D][·][图25]

31.如图26，在△ABC中，AB=6 cm，∠B=∠C，BC=4 cm，点D为AB的中点.若点P在线段BC上以1 cm/s的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动.

（1）若点Q运动的速度与点P运动的速度相等，经过1秒后，△BPD与△CQP是否全等？并说明理由.

（2）若点Q运动的速度与点P运动的速度不相等，当点Q运动的速度为多少时，△BPD与△CQP全等？ [A][B][C][D][P][Q]

32.如图27，点D在等边三角形ABC的边AB上，点F在边AC上，连接DF并延长交BC的延长线于点E，EF=FD.

求证：AD=CE. [A][B][C][D][E][F][图27]

33.问题引入：

（1）如图28，在△ABC中，点O是∠ABC和∠ACB平分线的交点，若∠A=α，则∠BOC= （用α表示）；如图29，∠CBO=[13]∠ABC，∠BCO=[13]∠ACB，∠A=α，則∠BOC= （用α表示）.

（2）如图30，∠CBO=[13]∠DBC，∠BCO=

[13]∠ECB，∠A=α，请猜想∠BOC= （用α表示），并说明理由.

类比探究：

（3）BO，CO分别是△ABC的外角∠DBC，∠ECB的n等分线，它们交于点O，∠CBO=[1n]∠DBC，∠BCO=[1n]∠ECB，∠A=α，请猜想∠BOC= . [A][D][E][B][C][O][A][B][C][O][B][C][O][A]