基于忆容器和忆感器的混沌振荡电路设计
臧寿池,王光义,史传宝
(杭州电子科技大学电子信息学院,浙江 杭州 310018)
基于忆容器和忆感器的混沌振荡电路设计
臧寿池,王光义,史传宝
(杭州电子科技大学电子信息学院,浙江 杭州 310018)
忆容器和忆感器是在忆阻器基础上定义的两种新型非线性记忆元件,目前未实现实际的忆容器和忆感器.为探究忆容器和忆感器在非线性电路中的特性,基于其数学模型设计了一个基于忆容器和忆感器的混沌振荡电路.通过对系统的分岔特性和Lyapounov指数等动力学特性的分析得出:在参数固定初始条件不同的情况下,系统出现了共存吸引子现象.对混沌系统进行了DSP实验验证,DSP实验结果与数值分析结果具有一致性.
忆容器;忆感器;混沌振荡器;共存吸引子
0 引 言
1971年,Leon O. C.[1]根据电路变量组合的完备性原理,从理论上预测了忆阻器的存在.2008年,HP实验室证实了忆阻器的存在[2].2009年,Ventra M. D.等[3]在忆阻器的基础上,进一步拓展了记忆元件的概念,提出了忆容器和忆感器的概念.目前对忆容器和忆感器的研究主要集中在其数学模型和电路模型[4-5].文献[6-8]提出了不同的忆容器模型并给出了SPICE仿真结果.文献[9]提出了忆阻器、忆容器、忆感器三者相互转换的方法.文献[10]分别对忆阻、忆容、忆感进行了物理分析,并用实例阐述了其物理特性.上述的研究都局限在单个元件的电路特性,并没有分析两个元器件同时运用在电路中的电路特性.
本文在文献[11]忆容器模型和文献[12-13]忆感器模型的基础上,构建一个基于忆容器和忆感器的混沌振荡电路.与一般混沌振荡系统相比,本文提出的混沌振荡系统对初始条件更加敏感,出现了共存吸引子现象.文献[14]基于忆阻器提出了一种新的混沌振荡系统并出现了共存吸引子现象,但其出现的共存吸引子现象是在电路参数变化的情况下出现的,没有说明初值变化时其运动轨迹可在不同的吸引子之间转换.
1 荷控忆容器和磁控忆感器
1.1 荷控忆容器
文献[12]根据荷控忆容器的定义方式,给出忆容倒数的一种表达式:
(1)
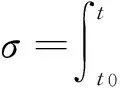
1.2 磁控忆感器
文献[13]根据磁控忆感器的定义方式,给出忆感倒数的一种表达式:
L-1(ρ)=c+dρ2
(2)
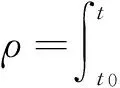
2 基于忆容器和忆感器的混沌振荡电路
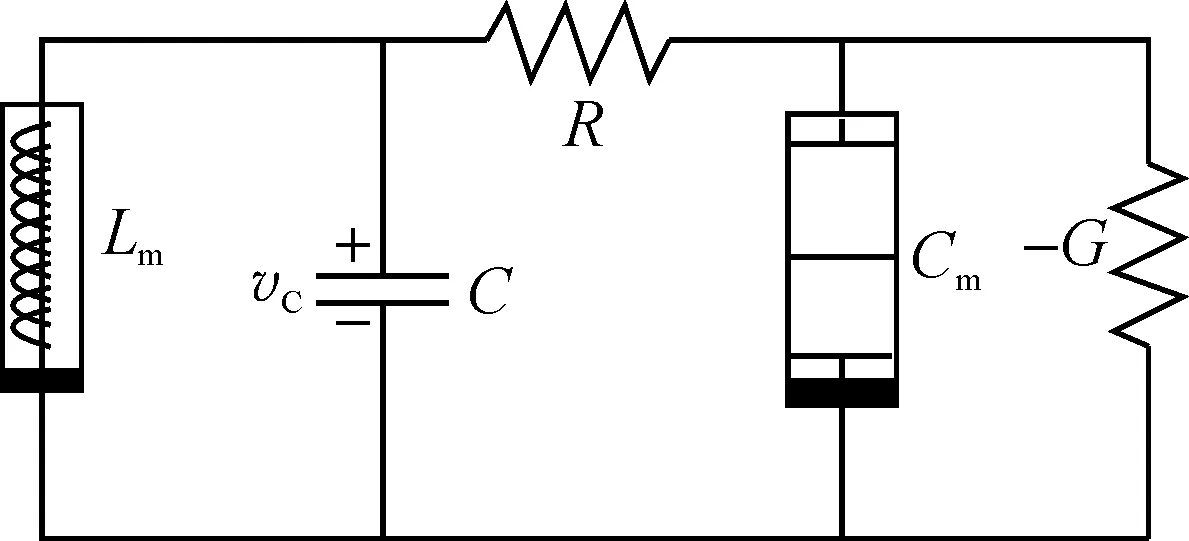
图1 忆容器和忆感器振荡电路图
本文设计的振荡器电路如图1所示.包括忆感器Lm,忆容器Cm,负电导-G,线性电阻R,线性电容C.
(3)
式中,iLm=(c+dρ2)φL,vCm=(α+βσC)qC.
当系统参数1/C=0.26 F-1,1/R=1.85 kΩ-1,α=5 F-1,β=3 F-1C-1s-1,c=10 H-1,d=20 H-1Wb-2s-2,G=1.65 mS,且初始状态为(0.00,-0.04,0.20,0.10,0.00)时,相应的Lyapunov指数为LE1=0.094 7,LE2=0.007 2,LE3=2.413 7e-005,LE4=-0.006 9,LE5=-1.113 9,则式(3)所描述的系统是混沌的,混沌吸引子相图如图2所示.
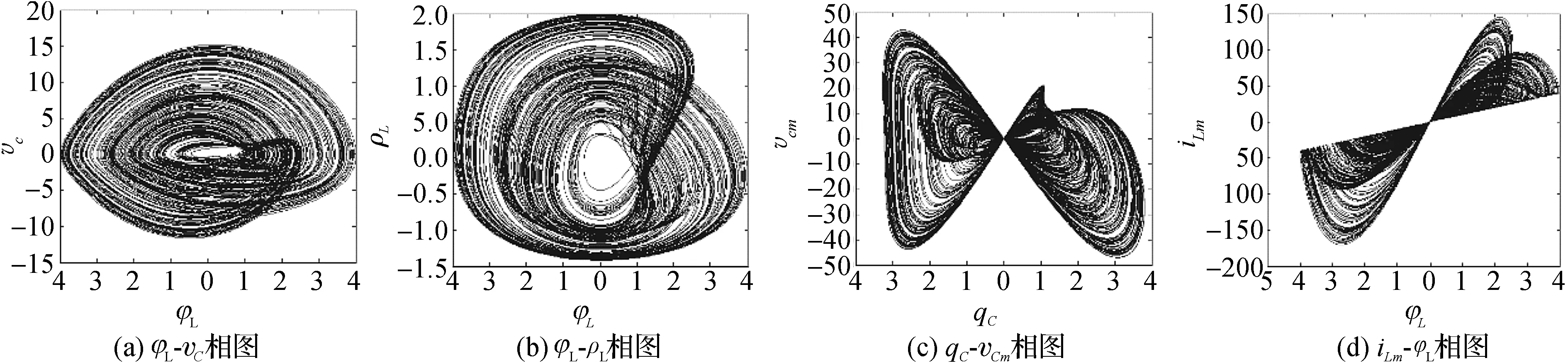
图2 混沌系统的混沌吸引子
3 平衡点集与稳定性
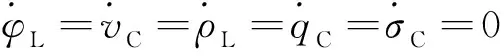
E={(φL,vC,ρL,qC,σC)|φL=vC=qC=0,ρL=k1,σC=k2}
(4)
位于ρL-σC平面上的每一个点均是平衡点,即该系统有无穷多个平衡点,其中k1和k2是实常数,式(3)在平衡点处的Jacobi矩阵J为
(5)
式中,m=α+βk2.
平衡点的特征根方程为:
λ2(λ3+a1λ2+a2λ+a3)=0
(6)
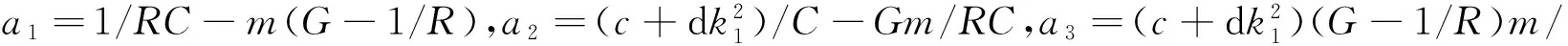
式(6)表明系统有2个零特征根和3个非零特征根.明显地,式(6)括号中的一元三次方程的系数都是非零的实常数,由劳斯-赫尔维茨(Routh-Hurwitz)判定可知,当系统处于混沌状态时,Δ1=a1,Δ2=a1a2-a3,Δ3=a3(a1a2-a3)三项应该不全为正.例如,当1/C=0.26 F-1,1/R=1.85 kΩ-1,α=5 F-1,β=3 F-1C-1s-1,c=10 H-1,d=20 H-1Wb-2s-2,G=1.65 mS,对于平衡点(0.00,0.00,0.20,0.00,0.00)有Δ1=1.481 0,Δ2=1.089 7,Δ3=-3.059 8,说明系统满足产生混沌的平衡点稳定性条件.
4 忆容器和忆感器混沌系统动力学分析
4.1 忆容器内部参数α对动力学特性的影响
固定参数1/C=0.26 F-1,1/R=1.85 kΩ-1,β=3 F-1C-1s-1,c=10 H-1,d=20 H-1Wb-2s-2,G=1.65 mS,且选择初始条件(0.00,-0.04,0.20,0.10,0.00),α在[2.0,5.1]范围内变化.状态变量φL随参数α变化的分岔图如图3所示,相应的Lyapunov指数谱如图4所示,为了图示清晰,始终最小的第5条Lyapunov指数没有画出.在α∈[2.0,5.1]范围内,系统由最初的周期状态经过倍周期分岔进入混沌状态.
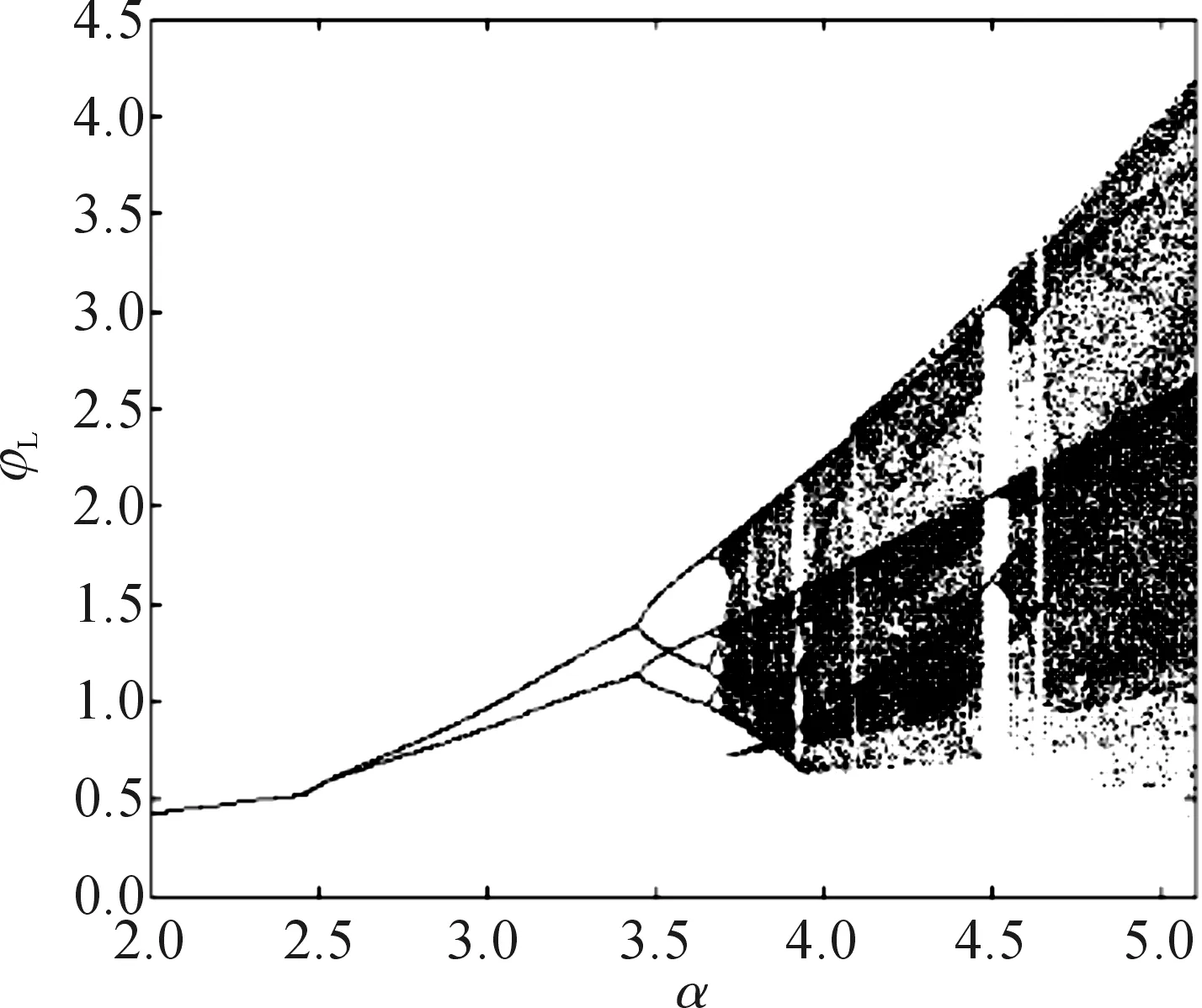
图3 分岔图

图4 Lyapunov指数谱
4.2 初始条件对动力学特性的影响
对于一般的混沌系统,其运动轨迹在同一吸引子内对初值是敏感的.其系统的轨迹不但在同一吸引子内对初值敏感,更重要的是初值变化时其轨迹可在不同的吸引子之间转换,即吸引子对初值具有高度敏感性,此为共存吸引子现象.
固定系统参数,当ρL(0)在[0.15,1.00]范围内变化时,系统的状态变量φL随ρL(0)变化的分岔图如图5所示,系统的Lyapunov指数谱如图6所示.随着ρL(0)的增大,系统的状态由混沌轨迹、倍周期轨道到周期轨道逐渐演变,这表明基于忆容器和忆感器的混沌振荡系统的状态不仅依赖于系统参数,同样也依赖于系统的初始条件.

图5 分岔图
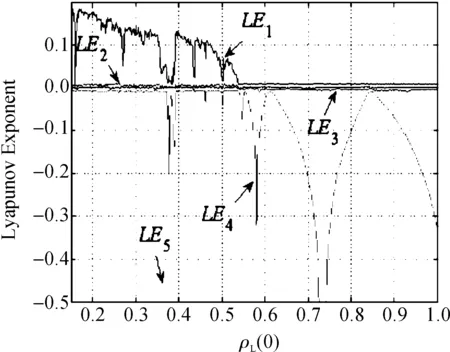
图6 Lyapunov指数谱
系统随着初始条件的变化共得到5种共存吸引子,如图7所示,表1列出了图7所得的吸引子与初始条件的对应情况.

图7 在不同初始条件下的吸引子相图

吸引子类型初始条件吸引子相图共存极限环(0.00,-0.04,0.90,0.10,0.00)(0.00,-0.04,0.90,0.10,-0.40)图7(a)极限环与点吸引子(0.00,-0.04,1.50,0.10,-0.40)(0.00,-0.04,0.90,0.10,-0.40)图7(b)混沌吸引子与极限环(0.00,-0.04,0.30,0.10,-0.40)(0.00,-0.04,0.90,0.10,-0.40)图7(c)混沌吸引子与点吸引子(0.00,-0.04,1.50,0.10,-0.40)(0.00,-0.04,0.20,0.10,-0.40)图7(d)共存混沌吸引子(0.00,-0.04,0.20,0.10,0.00)(0.00,-0.04,0.20,0.10,-0.40)图7(e)
5 忆容器和忆感器混沌系统的DSP实现
在DSP实验平台上验证忆容器和忆感器混沌系统,首先对忆容器和忆感器混沌系统进行离散化处理,将连续的混沌系统进行离散化,转换为离散混沌系统.在DSP平台上实现该离散混沌系统,并对其结果D/A转化,通过示波器观察其输出结果.DSP实验平台实验结果如图8所示,其结果和基于MATLAB的数值分析结果基本上是一致的.

图8 DSP实验结果
6 结束语
本文在忆容器和忆感器模型的基础上构建一个基于忆容器和忆感器的混沌振荡电路.通过数值仿真、平衡点求解与稳定性判断,以及通过分岔图与计算Lyapunov指数来分析基于忆容器和忆感器的混沌振荡电路的动力学行为.同时,通过DSP实验验证了实验结果与数值分析结果的一致性.本系统可以产生复杂的随机信号,用来生成性能良好的伪随机序列,在保密通信和信息加密中可以得到广泛的应用.
[1]CHUA L O. Memristor-the missing circuit element[J]. circuit theory, IEEE Transactions on, 1971,18(5):507-519.
[2]STRUKOV D B, SNIDER G S, STEWART D R, et al. The missing memristor found[J]. nature, 2008,453(7191):80-83.
[3]DI VENTRA M, PERSHIN Y V, CHUA L O. Circuit elements with memory: memristors, memcapacitors, and meminductors[J]. Proceedings of the IEEE, 2009,97(10):1717-1724.
[4]PEI J S, WRIGHT J P, TODD M D, et al. Understanding memristors and memcapacitors in engineering mechanics applications[J]. Nonlinear Dynamics, 2015,80(1/2):457-489.
[5]FOUDA M E, RADWAN A G. Memcapacitor response under step and sinusoidal voltage excitations[J]. Microelectronics Journal, 2014,45(11):1372-1379.
[6]BIOLEK D, BIOLEK Z, BIOLKOVA V. Behavioral modeling of memcapacitor[J]. Radio engineering, 2011,20:228-233.
[7]BIOLEK D, BIOLEK Z, BIOLKOVA V. SPICE modelling of memcapacitor[J]. Electronics letters, 2010,46(7):520-522.
[8]BIOLEK D, BIOLEK Z, BIOLKOVA V. SPICE modeling of memristive, memcapacitative and meminductive systems[C]//Circuit Theory and Design, 2009. ECCTD 2009. European Conference on. IEEE, 2009:249-252.
[9]YU D, LIANG Y, LU H H C. A Universal Mutator for Transformations Among Memristor, Memcapacitor, and Meminductor[J]. Circuits and Systems II Express Briefs, IEEE Transactions on, 2014,61(10):758-762.
[10]YIN Z Y, TIAN H, CHEN G H, et al. What are memristor, memcapacitor and meminductor?[J]. Circuits and Systems II Express Briefs, IEEE Transactions on, 2015,62(4):402-406.
[11]WANG G Y, CAI B Z, JIN P P, et al. Memcapacitor model and its application in a chaotic oscillator[J]. Chinese Physics B, 2016,25(1):489-500 .
[12]YUAN F, WANG G, JIN P, et al. Chaos in a Meminductor-Based Circuit[J]. International Journal of Bifurcation & Chaos, 2016,26(8):1650130.
[13]袁方,王光义,靳培培.一种忆感器模型及其振荡器的动力学特性研究[J].物理学报,2015,64(21):210504. CHEN M, LI M, YU Q, et al. Dynamics of self-excited attractors and hidden attractors in generalized memristor-based Chua’s circuit[J]. Nonlinear Dynamics, 2015,81(1/2):215-226.
[14]Chen M, Li M, Yu Q, et al. Dynamics of self-excited attractors and hidden attractors in generalized memristor-based Chua’s circuit[J]. Nonlinear Dynamics,2015,81(1/2):215-226.
Design of a Chaotic Oscillator Circuit Based on Memcapacitor and Meminductor
ZANG Shouchi, WANG Guangyi, SHI Chuanbao
(SchoolofElectronicInformation,HangzhouDianziUniversity,HangzhouZhejiang30018,China)
Memcapacitor and meminductor are two new nonlinear elements with memory, which are defined on the basis of the memristor and have not yet appeared. In order to explore the characteristics of memcapacitor and meminductor in nonlinear circuits, a chaotic oscillation circuit is designed based on the mathematical models of the memcapacitor and meminductor. The bifurcation characteristic and Lyapounov exponent of the chaotic system are analyzed, and the results show that the coexisting attractor phenomenon occurs when the initial conditions are different. Moreover, the chaotic system is verified by DSP experiment, and the result is consistent with numerical analysis.
memcapacitor; meminductor; chaotic circuit; coexisting attractor
10.13954/j.cnki.hdu.2017.03.002
2016-11-08
国家自然科学基金资助项目(60971046,61281230357);浙江省自然科学基金重点资助项目(LZ12F01001)
臧寿池(1991-),男,江苏射阳人,硕士研究生,非线性电路与智能信息处理.通信作者:王光义教授,E-mail:wanggyi@163.com.
TN401
A
1001-9146(2017)03-0006-05

