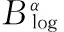QK(p,q)空间到Zygmund空间的Riemann-Stieltjes算子
高智娟,肖建斌,张彦林
(杭州电子科技大学理学院,浙江 杭州 310018)
QK(p,q)空间到Zygmund空间的Riemann-Stieltjes算子
高智娟,肖建斌,张彦林
(杭州电子科技大学理学院,浙江 杭州 310018)
通过选取QK(p,q)空间中的测试函数,利用算子理论和解析函数的性质,讨论了从QK(p,q)空间到Zygmund空间的Riemann-Stieltjes算子,并给出了该算子是有界算子和紧算子的充要条件.
QK(p,q)空间;Zygmund空间;Riemann-Stieltjes算子;有界性;紧性
0 引 言
解析函数空间上的算子理论是研究函数论中经典问题的重要工具.XIAO J.[1]首次提出Riemann-Stieltjes型算子,此算子是一种积分型算子和复合型算子,近些年来得到了广泛研究,其中LI S X.[2]研究了单位圆盘上加权Bergman空间和α-bloch空间之间的Riemann-Stieltjes型算子的有界性和紧性问题,文献[3-4]讨论了从混合模空间和Hardy空间到Zygmund型空间的Riemann-Stieltjes型算子的有界性和紧性问题.而对于QK(p,q)空间和Zygmund型空间,LIU Y M.[5]刻画了在单位球上乘子和径向导数算子的乘积在混合模空间到Zygmund型空间的有界性和紧性特征,YU Y Y.[6]给出了Bloch型空间和QK(p,q)空间之间的广义复合算子的本性模估计.本文讨论了QK(p,q)空间到Zygmund空间的Riemann-Stieltjes算子,并给出了刻画该算子是有界算子和紧算子的充要条件.
1 预备知识及引理
以D表示复平面上的单位圆盘,H(D)表示D上所有的解析函数.设K是定义在[0,+∞)上的右连续不减的非负函数,且满足
(1)
其中,χA(x)表示集合A的特征函数.p>0,q>-2,QK(p,q)空间定义如下

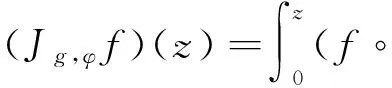
其中,f,g∈H(D),φ(D)⊂D.本文中C表示正常数,不同的地方可以不一样.
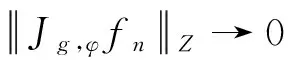

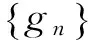
2 主要定理及证明
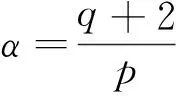
1)当p (2) 且 (3) 2)当p=q+2时,式(2)成立且 (4) 3)当p>q+2时,式(2)成立且 (5) 所以式(2)成立,即对于以上情况式(2)都成立. (6) 所以 再证充分性.由闭图像定理,只需证明对任意f∈QK(p,q),有Jg,φf∈Z.本文只证明p 1)当p (7) 且 (8) 2)当p=q+2时,式(7)成立且 (9) 3)当p>q+2时,式(7)成立且 (10) (11) (12) 令f(z)=1,f(z)=z,结合φ是D上的解析自映射可得 (13) (14) 因此,由式(11)—式(14)及文献[9]中的引理1得到 所以式(7)成立,对于以上情况,式(7)都成立. 1)当p 由定理1的证明知fn(z)∈QK(p,q),fn在D的任意紧子集上一致收敛于0,且 结合φ是D上的解析自映射及式(7)得到式(8)成立. 2)当p=q+2时,取函数 则fn(z)∈QK(p,q),与1的情形类似证明,可得式(9)成立. 3)当p>q+2时,取fn(z)=1,可得式(10)成立.证毕. Riemann-Stieltjes型算子作为复合算子的推广,研究其在两个解析函数空间之间的有界性和紧性是有意义的,本文讨论了Riemann-Stieltjes型算子在QK(p,q)空间到Zygmund空间上的有界性与紧性,将进一步研究其在QK(p,q)空间到小Zygmund空间上的有界性和紧性问题. [1]XIAOJ.Riemann-StieltjesoperatorsonweightedBlochandBergmanspacesoftheunitball[J].JournaloftheLondonMathematicalSociety, 2004,70(1):199-214. [2]LIS.VolterracompositionoperatorsbetweenweightedBergmanspacesandBlochtypespaces[J].JournaloftheKoreanMathematicalSociety, 2008,45(1):229-248. [3]LIUY,LIUH.Volterra-typecompositionoperatorsfrommixednormspacestoZygmundspaces[J].ActaMathematicaSinica, 2011,54(3):381-396. [4]刘永民,郭健.Hardy空间到Zygmund型空间的Riemann-Stieltjes算子[J].数学学报,2014,57(4):693-708. [5]LIUY,ZHOUJ.OnanOperatorMuRfromMixedNormSpacestoZygmund-TypeSpacesontheUnitBall[J].ComplexAnalysisandOperatorTheory, 2013,7(3):593-606. [6]YUY,LIUY.TheEssentialNormofaGeneralizedCompositionOperatorBetweenBloch-TypeSpacesandQKTypeSpaces[J].ComplexAnalysisandOperatorTheory, 2012,6(6):1231-1240. [7]KOTILAINENM.OncompositionoperatorsinQKtype spaces[J]. Journal of Function Spaces, 2007,5(2):103-122. [8]DUREN P L. Theory of Hp spaces[M]. New York: Academic press, 1970:71-92. Riemann-Stieltjes Operator fromQK(p,q) Space to Zgymund Space GAO Zhijuan, XIAO Jianbin, ZHANG Yanlin (SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China) By choosing testing function ofQK(p,q) space and using operator theory and the properties of analytic function, this paper discusses Riemann-Stieltjes operator fromQK(p,q) space to Zgymund space, and the necessary and sufficient conditions for the boundedness and compactness of the operators are obtained. QK(p,q) space; Zgymund space; Riemann-Stieltjes operator; boundedness; compactness 10.13954/j.cnki.hdu.2017.03.019 2016-10-18 国家自然科学基金资助项目(11571104);浙江省大学生科技创新活动计划(新苗计划)资助项目(2016R407079) 高智娟(1992-),女,河北唐山人,硕士研究生,复分析及其应用.通信作者:肖建斌教授,E-mail:xjb@hdu.edu.cn. O177.2 A 1001-9146(2017)03-0091-05
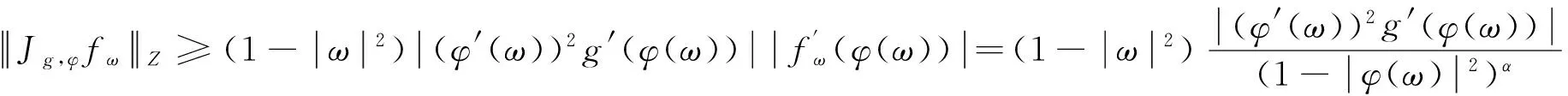

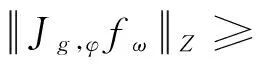
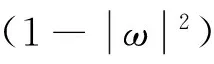

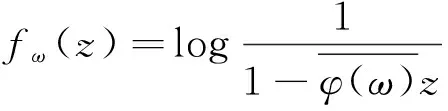

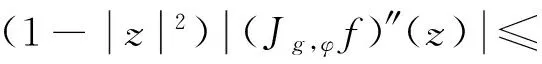
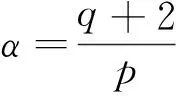
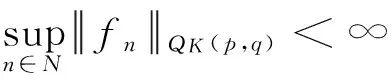
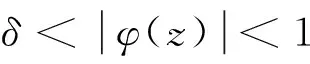


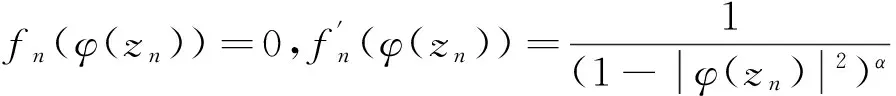
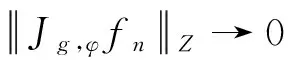
3 结束语