跨临界CO2引射制冷系统控制性能

何 阳张早校，邓建强

（1西安交通大学动力工程多相流国家重点实验室 西安 710049；2西安交通大学化学工程与技术学院 西安 710049）

跨临界CO2引射制冷系统控制性能

何 阳1张早校1，2邓建强2

（1西安交通大学动力工程多相流国家重点实验室 西安 710049；2西安交通大学化学工程与技术学院 西安 710049）

本文建立了两种控制器（单通道最优控制器（SCOC）和多变量线性二次高斯控制器（LQG））以改善跨临界CO2引射制冷系统的运行效率。首先建立了SCOC，通过在线调节喷嘴喉部面积，搜索系统最优的气冷器压力；其次针对SCOC作用下制冷量不可控的缺点，设计了LQG以实现系统制冷量可调。将两种控制器分别应用于实验系统中，结果表明：SCOC能够驱使系统不断接近系统的最优气冷器压力，给定工况下获得最大制热系数COPh为3.15，但导致系统制冷量的不可控。在LQG的作用下，气冷器压力、系统制冷量得到独立控制，显示了很好的参数跟随性，然而LQG无法保证系统的稳态运行效率。研究指出两种控制器各有优缺点，若实现满足系统负荷需求的同时保持系统最高的运行效率，需要设计结合两种算法特点的新型控制器。

制冷；引射器；CO2；优化控制；多变量控制器

CO2作为自然工质，无毒，对环境污染小，是一种理想的制冷剂。然而CO2高临界压力、低临界温度的特点，使得跨临界CO2循环中节流损失严重，系统的性能低于常规制冷工质系统［1］。引射器作为一种结构简单的压力能回收装置，对CO2循环性能的改善显著，能够使CO2系统获得与常规工质系统相当的性能［2－5］。然而，引射器工作特性特殊，不同工况下固定结构的引射器性能变化较大［6］。C.Lucas等［7］通过实验研究发现，最佳工况下引射器的引入可使常规CO2蒸气压缩循环COP提高17%；而在某些工况下，引射器却降低了系统性能，可使COP降低超过5%。因此，固定结构引射器的引入会使系统适用工况范围变窄。

裴文伟等［8］通过实验研究发现，在给定工况下，调节喷嘴喉部面积可以显著影响引射器和系统的性能。S.Elbel等［9］针对跨临界CO2引射制冷系统设计了喷嘴喉部可调的引射器，并通过调节喉部面积获得了不同环境温度下对应的最优气冷器压力，从而获得了更好的系统COP。X.X.Xu等［10］在CO2热泵热水器中采用相同的可调引射器，通过实验得到了不同供热量下的最优气冷器压力，并拟合了经验公式，为控制系统的设计提供了依据和指导。可调引射器可以有效地保证引射器在不同工况下的正效应，扩大引射系统的适用工况，对进一步改善引射系统工作性能有重要意义。

可调引射器的实际应用需要配套自动控制系统，以保持制冷或热泵系统在不同工作环境和负荷下的高效运行，目前未见相关的文献发表。本文基于带可调喷嘴的跨临界CO2引射制冷系统的动态模型，分别建立了单通道级联最优控制器（SCOC）及多变量LQG控制器，并比较了两种控制器的优缺点，从控制角度分析提高引射制冷系统效率的可能性，对CO2引射系统的控制策略提出了建议。

1 实验系统及动态模型

图1所示为跨临界CO2引射制冷循环流程，蒸发器的热源及气冷器的冷却液均为水。系统中喷嘴喉部面积、压缩机转速、膨胀阀开度为系统内部的可调参数，可作为控制系统的执行器。

图2所示为可调引射器的具体结构尺寸。该引射器喷嘴中添加了尖端带锥度的阀针，系统通过步进电机旋转阀针调节阀针尖端的位置，调节精度为5 μm，从而控制主动流在喷嘴喉部的流通面积，直接影响高压侧CO2流量及气冷器压力。以阀针尖点在喉部位置时阀针位置x＝0 μm，随着阀针旋入，阀针位置x增加，主动流喉部流通面积可由式（1）计算。

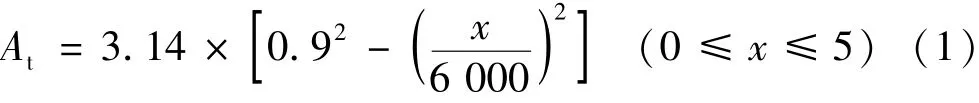
图2 可调引射器结构图（单位：mm）Fig.2 The diagram of the adjustable ejector

系统中其他设备的具体参数见表1。水系统为开式系统，流量通过玻璃转子流量计进行调节，供水温度由PID温控仪控制加热器进行调节，从而为系统提供可变的工作环境及负荷，同时水流量的波动也是系统扰动的主要来源。系统所用的传感器型号及精度如表2所示。需测量的变量通过Kethley 2700数据采集仪和7700板卡进行采集，并通过RS232接口与电脑连接进行数据记录。

系统动态模型是控制系统设计的基础。对于压缩机、膨胀阀和引射器相对换热器而言，时间常数很小，因此在动态模型中采用稳态模型；蒸发器采用相界面移动模型；而气冷器中没有相变换热，采用集总参数模型；气液分离器则根据能量、质量守恒建立动态模型。根据各组件之间的能量及质量守恒关系，耦合各组件模型从而建立系统动态模型。模型的数学公式和所采用参数在本课题组之前的工作中已有发表［12］。

表1 实验台各设备参数［11］Tab.1 Parameters of experimental devices

表2 传感器参数Tab.2 The parameters of the sensors

2 控制系统

针对系统效率最优化和系统负荷定量可调分别设计了两种控制系统：单通道级联最优控制器（SCOC）和多变量LQG（线性二次高斯控制器）控制器。默认情况下，本文所采用工况为冷却水进口温度24℃，流量为1.75 L／min，冷冻水进口温度为22℃，流量为4 L／min。系统的初始状态为：压缩机转速为1 400 r／min，膨胀阀开度为50%；喷嘴喉部面积为0.88 mm2。

2.1 SCOC

与常规制冷剂系统不同，CO2系统中采用了气冷器而非冷凝器，使其高压侧压力不受外侧温度影响，显著地影响着系统的性能，其相关优化控制研究已有开展［13－15］。 同样的，在 CO2引射循环中，气冷器压力极大地影响着系统运行效率［16－17］。在引射系统中，喷嘴取代膨胀阀与气冷器直接相连，喷嘴喉部面积的变化将直接作用于气冷器，从而影响系统的工作状态及性能［5］。本文据此设计了以气冷器压力为控制对象、可调喷嘴为执行器、以最高COP为控制目标的单通道级联最优控制器。如图3所示，所设计控制系统包括三个部分：PID算法、压力预测器、被控系统。此控制器的设计不依赖于系统的结构和尺寸，结构简单。考虑到引射系统非线性强烈，跟随器采用自适应PID算法。

图3 单通道级联最优控制器Fig.3 Single channel cascade optimal controller

制冷剂CO2质量流量测量成本高，制热系数的计算仅使用制冷剂高压侧流量，在计算式中可以约去，所以本文采用制热系数描述系统性能：

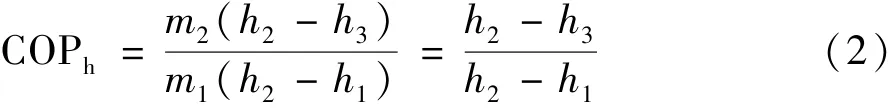
式中：下标 1，2，3为系统中对应的状态点（图1）。

以气冷器压力为变量，采用最优梯度法寻找最优气冷器压力：

式中：α为步长，其大小直接影响着算法的控制效果；下标n为迭代标识。此外，

在该控制器设计中，首先采用临界比例法设计跟随器中的PID参数，获得最优值后再设计预测器的步长参数。经过多次模拟比较，最终采用预测器步长α＝0.3，采样周期为15 s，PID跟随器采样周期3 s，积分时间常数20 s，微分时间常数0.3 s，以及比例项：

Kp＝－0．01p2gc＋0．26pgc－1．67 （5）

SCOC控制器通过调节喷嘴喉部面积，控制气冷器压力，使得系统最终工作于COP最佳的状态下。图4所示为不同喷嘴喉部面积下实验系统达到稳定时的气冷器压力和对应COPh。结果显示存在最佳的喷嘴喉部面积使得系统运行效率最高。本文所选工况下，最佳喉部面积为0.58 mm2，对应的气冷器压力为11.3 MPa，此时系统最大的运行效率 COPh＝3.155。

图4 不同喷嘴喉部面积对系统稳态的影响Fig.4 Steady states for different nozzle throat areas

图5所示为SCOC控制器作用下，实验系统由初始状态向最优点变化的动态过程。随着控制器的启动，喷嘴喉部面积不断变化，系统呈逐渐变弱的震荡趋势逐步跟随所预测的气冷器压力，直到系统COPh达到最大。系统稳定后，对应气冷器压力为11.17 MPa，COPh为3.15，与图4所得最优工况一致，此时对应的喷嘴喉部面积约为0.602 mm2。该控制器作用下系统由初始状态达到最优稳定点的稳定时间约435 s。SCOC控制器的设计不依赖于被控对象的模型，只需依据经验调节几个参数即可应用于另外不同的系统，设计过程简单，应用成本低。

然而，随着控制器的运行，蒸发器出水温度由7.5℃逐渐变为5.4℃，系统制冷量增加了12.7%。因此，尽管SCOC控制器能够很好地自动寻找系统最优工况点，但是制冷量也会随之变化，可能会增加或减少，在实际应用中受到限制。

图5 SCOC控制器作用下系统的动态过程Fig.5 Dynamic process of the system under SCOC

2.2 多变量LQG控制器

引射制冷系统中，各变量参数之间耦合关系复杂，SCOC控制器在改变被控变量的同时会引起其他变量的变化，无法满足多个变量的同时调节。为此，进一步设计了多变量LQG控制器（图6），通过调节喷嘴喉部面积An和压缩机转速w，实现气冷器压力、蒸发器出水温度（或系统制冷量）的同时调节。

图6 LQG控制器简图Fig.6 Schematic diagram of LQG controller

如图6所示，该控制器由3部分组成：基于Kalman滤波算法的状态预估器、LQR（线性二次控制器）状态反馈器以及基于积分的误差补偿器。该控制器的设计系统的线性动态模型，基于课题组之前的所建立的动态模型［11］，系统的线性动态模型可根据泰勒展开获得：

式中：x为系统状态向量，具体见文献［11］；u为系统输入向量，且u＝［w，An］；y为系统输出，且y＝［T9，p2］，矩阵A、B、C、D为线性模型的系数矩阵，用于建立图6中的Kalman状态预估器。基于此线性方程，利用MATLAB控制工具箱设计Kalman状态预估器，从而可依据所测输出及输入估算所需的状态值。状态反馈矩阵Kr的计算需要考虑积分过程。采用扩展的状态向量＝［x，y～］，其中y～·＝r－y，在原状态空间模型基础上重新构建新的线性模型，基于线性二次高斯控制理论（MATLAB工具箱），可以计算得到反馈矩阵。

采用设计的LQG控制器，改变气冷器压力、蒸发器出水温度（制冷量）的设定值，系统的动态调节如图7所示。结果显示控制器能保持较好的参数跟随性，系统稳定时间约100 s。此外，当气冷器压力目标值突变时，LQG控制器能够很好的保持蒸发器的出水温度不变，由于蒸发器的进水温度和流量已经设定不变，可保证系统的制冷量不变。同样的，系统所需制冷量突变的情况下，气冷器压力在LQG作用下也能够快速恢复设定值。因此采用LQG控制器，可实现气冷器压力、系统制冷量（或蒸发器出水温度）的独立控制。

图7 LQG控制器参数跟随性Fig.7 Parameters tracking of LQG controller

图8所示为对应的压缩机转速和喷嘴喉部面积的变化过程。可知在20 s时系统目标制冷量升高（蒸发器出水温度降低），控制器作用下压缩机转速增加，引起气冷器压力的突然升高，此时喷嘴喉部面积骤增，导致气冷器压力降低，之后随着压缩机转速增加，气冷器压力逐渐恢复到设定值；在220 s时，气冷器压力设定值降低，喷嘴喉部面积快速增加，导致系统制冷量降低，蒸发器出水温度升高，此时在LQG控制器作用下压缩机转速增加，从而保证了系统的制冷量。考虑压缩机转速变化过大会影响压缩机寿命并且增加能耗，LQG设计过程中有意将更多的控制动作作用于喷嘴喉部面积，从而降低了动态调节过程中的能耗。

图8 执行器的动态调节过程Fig.8 Dynamic process of the actuator

与SCOC控制器相比，LQG可以在保证系统制冷量的前提下，自动调节气冷器压力到设定值。然而LQG的设计仅考虑动态调节过程中的能耗，无法保证系统在稳定后获得最佳的运行效率。此外，LQG的设计极大的依赖于动态模型的精确性，其设计过程相对复杂。两种控制器各有优缺点，但都无法使系统在设定制冷量需求的条件下保持系统最高的运行效率，因此将两种控制器相结合提出一种新的控制器对扩展引射器的有效工况范围、提高引射系统的实际运行效率有重要意义。

3 结论

可调引射器对扩展引射制冷系统有效工况范围、提高引射系统运行效率有重要作用。本文针对带可调引射器的跨临界CO2引射制冷系统，设计了两种控制器：单通道最优控制器（SCOC）和多变量线性二次高斯（LQG）控制器。采用固定的压缩机转速、膨胀阀开度及外部水工况下进行实验研究，结果表明：SCOC通过调节喷嘴喉部面积，能够很好的驱动引射系统在最优气冷器压力下工作，最大制热系数COPh可达3.15，与稳态实验结果一致，然而该过程导致制冷量不可控的增加了12.7%；而LQG控制器在保证制冷量的同时可以很好的调节气冷器压力，有很好的参数跟随性，但是气冷器压力需人为设定，无法主动维持系统的稳态效率。两种控制算法各有优缺点，没有实现实际应用中变工况下的高效运行。因此需要提出一种结合两种算法特点的新型控制器，使系统在保证制冷量的同时获得最高的稳态运行效率，有效推动引射系统的商业化应用。

［1］李倩，郭宪民，李卫国，等.跨临界CO2两相流引射制冷系统性能实验研究［J］.制冷学报，2012，33（5）：15-19.（LI Qian，GUO Xianmin，LI Weiguo，et al.Experimental investigation on the performance of the transcritical CO2two-phase ejector refrigeration cycle［J］.Journal of Refrigeration，2012，33（5）：15-19.）

［2］Sun F T，Ma Y T.Thermodynamic analysis of transcritical CO2refrigeration cycle with an ejector［J］.Applied Thermal Engineering，2011，31（6／7）：1184-1189.

［3］Lee J S，Kim M S，Kim M S.Experimental study on the improvement of CO2air conditioning system performance using an ejector［J］.International Journal Refrigeration，2011，34（7）：1614-1625.

［4］He Y，Deng J Q，Zhang Z X.Thermodynamic study on a new transcritical CO2ejector expansion refrigeration system with two-stage evaporation and vapor feedback［J］.HVAC＆R Research，2014，20（6）：655-664.

［5］郑立星，邓建强，何阳.两级蒸发对跨临界CO2引射制冷系统影响的实验研究［J］.制冷学报，2015，36（4）：66-71.（ZHENG Lixing，DENG Jianqiang，HE Yang.Experimental investigation on the effect of the second stage evaporation on the transcritical CO2ejector expansion refrigeration system ［J］.Journal of Refrigeration，2015，36（4）：66-71.）

［6］Elbel S.Historical and present developments of ejector refrigeration systems with emphasis on transcritical carbon dioxide air-conditioning applications［J］.International Journal of Refrigeration，2011，34（7）：1545-1561.

［7］Lucas C，Koehler J.Experimental investigation of the COP improvement of a refrigeration cycle by use of an ejector［J］.International Journal of Refrigeration，2012，35（6）：1595-1603.

［8］裴文伟，郭宪民，王善云，等.几何参数对引射器及两相流引射制冷系统性能的影响［J］.制冷学报，2013，34（1）：65-68.（PEI Wenwei，GUO Xianmin，WANG Shanyun，et al.Effects of geometric parameter on performance of ejector and two-phase ejector refrigeration system［J］.Journal of Refrigeration，2013，34（1）：65-68.）

［9］Elbel S，Hrnjak P.Experimental validation of a prototype ejector designed to reduce throttling losses encountered in transcritical R744 system operation［J］.International Journal of Refrigeration，2008，31（3）：411-422.

［10］Xu X X，Chen G M，Tang L M，et al.Experimental investigation on performance of transcritical CO2heat pump system with ejector under optimum high-side pressure［J］. Energy，2012，44（1）：870-877.

［11］何阳，张早校，薛长乐，等.基于延迟均衡的CO2两相引射器模型研究［J］.制冷学报，2016，37（4）：1-6.（HE Yang，ZHANG Zaoxiao，XUE Changle，et al.A CO2two-phase ejector model based on delayed equilibrium model［J］.Journal of Refrigeration，2016，37（4）：1-6.）

［12］Zheng L X，Deng J Q，He Y，et al.Dynamic model of a transcritical CO2ejector expansion refrigeration system［J］. International Journal of Refrigeration，2015，60：247-260.

［13］宋昱龙，唐学平，王守国，等.跨临界CO2热泵气体冷却器对系统性能及最优排气压力的影响［J］.制冷学报，2015，36（4）：7-15.（SONG Yulong，TANG Xueping，WANG Shouguo，et al.The effects of the gas cooler on both the system performance and the optimal discharge pressure at a transcritical CO2heat pump［J］.Journal of Refrigeration，2015，36（4）：7-15.）

［14］Chen Y，Gu J J.The optimum high pressure for CO2transcritical refrigeration systems with internal heat exchangers［J］.International Journal of Refrigeration，2005，28（8）：1238-1249.

［15］胡斌，李耀宇，曹锋，等.跨临界CO2热泵系统最优排气压力的极值搜索控制［J］.制冷学报，2016，37（3）：81-87.（HU Bin，LI Yaoyu，CAO Feng，et al.Extremum seeking control of discharge pressure optimization for transcritical CO2heat pump systems［J］.Journal of Refrigeration，2016，37（3）：81-87.）

［16］Deng J Q，Jiang P X，Lu T，et al.Particular characteristics of transcritical CO2refrigeration cycle with an ejector［J］.Apply Thermal Engineering，2007，27（2／3）：381-388.

［17］Li D Q，Groll E A.Transcritical CO2refrigeration cycle with ejector-expansion device［J］.International Journal of Refrigeration，2005，28（5）：766-773.

Control Performance of Transcritical CO2Ejector Refrigeration System

He Yang1Zhang Zaoxiao1，2Deng Jianqiang2
（1.State Key Laboratory of Multiphase Flow in Power Engineering，Xi′an Jiaotong University，Xi′an，710049，China；2.School of Chemical Engineering and Technology，Xi′an Jiaotong University，Xi′an，710049，China）

Two controllers（single channel optimal controller（SCOC）and multivariable linear quadratic Gaussian controller（LQG））are built to improve the performance of a transcritical CO2refrigeration cycle.The SCOC is first proposed to search the optimal gas cooler pressure online by adjusting the nozzle throat area.Considering the uncontrollable cooling capacity by the SCOC，the second controller LQG is designed to achieve the controllable cooling capacity.Experimental results show that the optimal gas cooler pressure is actually achieved by the SCOC with a maximal COPhof about 3.15 under the given operating conditions.However，with the SCOC，the cooling capacity is changed passively and uncontrollably.Moreover，experiments with LQG indicate that the cooling capacity and gas cooler pressure are accurately tracked independently.However，LQG cannot ensure the maximal operating performance when the system becomes steady.This work points out that the two controllers have their own advantages and disadvantages.More work needs to be done to combine the two algorithms into one.This will achieve maximal efficiency under the desired cooling capacity.

refrigeration；ejector；CO2；optimal control；multivariable controller

TB61；TB675.5；TB61＋1

：A

0253－4339（2017）03－0001－06

10.3969／j.issn.0253－4339.2017.03.001

邓建强，男，教授，西安交通大学化学工程与技术学院，（029）82663413，E-mail：dengjq＠mail.xjtu.edu.cn。研究方向：高效化工机械与设备。

国家自然科学基金 （51676148）资助项目。（The project was supported by the National Natural Science Foundation of China（No. 51676148）.）

2016年10月20日

About the corresponding author

Deng Jianqiang，male，professor，School of Chemical Engineering and Technology，Xi′an Jiaotong University，＋86 29-82663413，E-mail：dengjq＠ mail.xjtu.edu.cn.Research fields：efficient chemical machineries and equipment.