基于数学名题的思维课堂实践研究

◎蒋巧君

基于数学名题的思维课堂实践研究

◎蒋巧君

“知识是手段，不是目的。思维才是最有效的。”但思维的隐形性增加了思维培养的难度。数学课堂上很多学生学习“抄近路”，回答问题只说答案。教师追问思考过程，学生表述不清，缺乏表达思考过程的能力。正因为抽象的思维隐形于学生的学习活动中，教师不能准确地把握学生的思维动态。更何况学生思维品质的提升，不是一朝一夕的事，是一个长期积累的过程。一节课的效果不能立竿见影，所以思维品质的培养容易被教师们忽视。如何建构思维课堂，提升学生思维品质呢？

一、为学生提供有思考价值的素材

数学名题是数学发展史中有一定的历史故事与情节，有数学著作记载或民间流传的有代表性的数学问题。如鸡兔同笼、李白喝酒、以碗知僧、百钱白鸡、韩信点兵……数学题之所以能成为名题 ,大多数是因富含哲理且寓于生活之中 ,读之妙趣横生而又回味无穷，因此很多名题都是大家所喜闻乐见的。教师要以数学名题为载体，适当介绍有关的背景知识，帮助学生感悟深厚的数学文化，体会数学在人类发展史中的作用。思维课堂要实现的条件是教师要掌握核心技术：教师自身提问的技术和激发学生提问的技术。一名优秀的教师，应该是学生思维的激发者，要让学生有适当的时间和空间自主发问“为什么”。这样才能引出学生更多的想法。如果教师的提问马上能让全体学生举手回答，那不是好问题。主题式的数学名题往往是个大问题，能让学生进入探究之中。

二、促使学生从低阶思维迈向高阶思维

“小先生学习模式”是最高品质的学习。基于“数学名题”经典的学习载体，通过学生“独立自主研读——小组交流合作探究——小先生汇报解说——同伴认真倾听质问——全班师生多维互动研讨”，不断刺激学生的大脑，改变学生的线性思维，实现网状联结，形成高阶思维。思维层次有高低之分，而思维方法没有好坏之分，运用哪种思维方法解决什么问题却有决策优劣之别。罗列出可解决问题的种种方法，选用最合理的思维方法解决问题，这是思维动态的决策能力。久而久之，这种思维能力渐渐成为不容易改变的一种惯性，即思维品质。思维的独创性、灵活性、敏捷性、深刻性、批判性……影响学生一生的学习、工作与生活。这就是我们所要追求的学生的核心素养。不唯书，不唯师，不唯上的批判性思维的培养，能让学生张开创造、想象的思维翅膀。

三、指导学生学会表示思考过程的方法

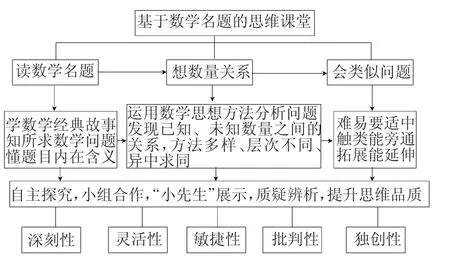
根据以上要素的理论分析与课堂实践，笔者经过几年来的总结，提炼形成了“基于数学名题的思维课堂”模式。

（一） 读有价值的数学名题

“鸡兔同笼”问题是我国民间广为流传的数学趣题，最早出现在《孙子算经》中，如今被编入到北师大版、苏教版、人教版、北京版等不同版本不同年级的教材中。如何充分利用数学名题“鸡兔同笼”在不同年级进行不同思维方法的有效引导呢？要遵循儿童的认知规律，科学合理地品读数学名题。我们安排了三、四、五、六年级学生让四位教师同课异构，根据各个层次的年龄特征定位不同的学习目标。三年级目标为画图策略；四年级的目标为从逐一列表假设拓展到跳跃列表假设；五年级的目标定位为灵活运用逐一、折中和跳跃假设法，并学会用两步假设来推理出正确答案，过渡到算术假设法；六年级的目标则定位为方法上的求联，通过比较画图、列表、算术推理、方程假设等各种方法，把所有的方法上升为一种假设的上位思想。学生思维发展由具体到抽象的过程显露无疑，充分体现了鸡兔同笼的思维价值。由此可见，不同年级确定不同目标，采用不同方法品读数学名题，符合学生的认知特点，也能真正读懂数学名题。

（二） 想已知与未知数量之间的关系

引导学生合理选用分析法、综合法、假设法等数学思想方法发现数量之间的关系。《鸡兔同笼》这一数学名题的关键是让学生“自主探究、小组合作、小先生展示、质疑辨析”，引导学生在运用假设法的同时，要化无形的思维为有形思维，理清已知与未知之间的数量关系。思维本身就是无形的，如果教师能在实施过程中化无形为有形，势必会让学生的思维增量。如三年级的课中采用画图的策略来解决问题，针对画图一次不能到位而需要调整时，教师可用不同颜色的粉笔标出脚太多时把兔调整为鸡，或者可以用圈的方法在旁边标注调整的过程，这样学生的思维过程就表达出来了。四年级的课中，学生出现图1情况，教师应该适时地让孩子回到鸡兔画图的过程，来理解“脚少了怎么办？加兔减鸡。”

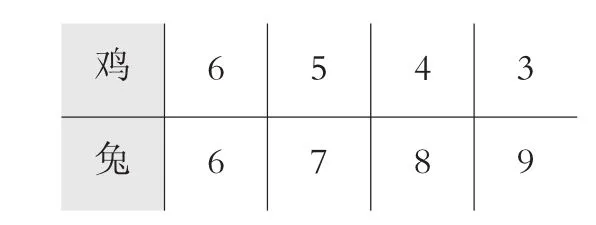
图1

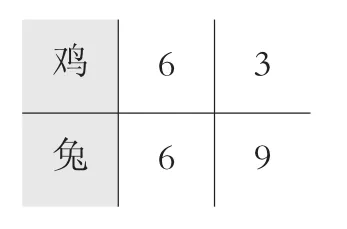
图2

如图2，学生的回答是通过2次折中假设得出正确答案，此时，教师可顺势质疑，为什么鸡的只数再次取半，而不往上推理呢？因为脚数太少，要增加兔的数量，从而发展学生的逻辑推理能力。

五年级的课堂如图3：通过教师的表格数据比对，调整过程用箭头显现，学生调整的过程一目了然，理解起来显得轻松。两步列表法发展到算术法只差临门一脚，因此，通过两步列表法理解过程，算术法来总结，思维过程就水到渠成了。

图3

从课初的随意猜想到表格中的有序猜想，从一般验证到表格中数据变化规律的发现，从列表法自然联想到假设法，学生的思维经历了从无序到有序、从特殊到一般、从借鉴到创新、从肤浅到深刻的巨大变化，学生的思维能力也随之得到了极大的提升。

（三） 能触类旁通和拓展延伸

三、四、五年级的课堂中呈现了大量的素材，教师需要帮助学生举一反三建立鸡兔同笼的模型，如：日本的龟鹤算、三轮车和自行车同轮分配、人民币混装问题都属于鸡兔同笼模型下的思维拓展。面对这些问题，引导学生给“鸡兔同笼”重新取名。不经意的点拨，适时的追问，让学生一次次跳出那只有形的“笼子”，超越具体的解题方法，上升为一种更具有普适性的思想方法与策略——假设，从而建构起解决这类问题的更具有一般性的“数学模型”，通过方法迁移，会一题，通一类。

（作者单位：浙江省义乌复旦实验学校）

（责任编辑：杨强）