从原型到模型：让学生经历几何抽象的过程

◎李 芳

从原型到模型：让学生经历几何抽象的过程

◎李 芳

抽象出射线、直线的几何特征，理解其本质含义对学生而言并不容易。教学过线段、射线、直线相关内容的教师往往会有这样的经验：学生会误认为线段就是一根毛线，射线就是激光笔发射出的光线，认为黑板上所画的直线长度是有限的，当学习射线、直线的时候，二年级学过的线段又有所遗忘。因此，在教学中，有必要对线段的相关知识做简要复习，并进一步帮助学生认识线段、射线、直线的几何模型本质。那么如何选择合适的线段、射线、直线的几何原型？在具体教学中，怎样从原型抽象为模型又不为原型所困惑？

一、选择几何原型，需要从学生出发，以史为鉴

（一） 要尊重儿童认知规律和生活经验

中高年级小学生思维呈现的特点是从具体形象思维向抽象思维过渡，他们的抽象逻辑思维依然需要与感性经验相联系。

苏教版教材在二年级“认识线段”的设计上，就采取了用一段拉直的毛线帮助学生提取线段的典型特征；到了四年级“认识射线”时，又借助了激光的形象，帮助学生认识射线。对于直线，则采用了延长线段两个端点的方法帮助学生来认识。这样处理确实有其合理性。但在实际教学中，学生对于直线的认识往往存在困难。因此，有必要为学生提供生活中一些近似直线的原型，帮助学生理解直线的特征。

（二） 要以数学史的发展为蓝本

当今的数学界普遍认为，几何发源于古代埃及，是埃及人在丈量土地的需要中产生的。而几何中线段、射线、直线的几何雏形则伴随着人类绘画的产生而产生，古人用近似线段的短线表示物体的边沿，用近似射线的线条表示太阳发出的光线，用近似直线的线条来表示地平线。可以说，没有的现实雏形，就没有几何图形的诞生。但线段、射线、直线却并非这些线本身。根据量子物理学的发展可知，光子在宇宙中的运行并非沿直线运动的，而是会发生偏折的。因此，线段、射线、直线在现实世界中是无法给出精确定义的。从本质而言，几何学是人脑推理的产物，数学是对客观世界的理性、抽象思考的产物，我们画下来的线段、射线、直线只是线段、射线、直线的一种表示方式。

（三） 要做出合理解释

鉴于以上两点，我借鉴了教材中射线的原型，并采用了海天交界线，地平线的直线原型。在这里需要解决一个问题，几乎所有的学生都知道地球是圆的，也知道海和大地都是有边际的，这个素材要如何使用呢？一方面需要借助学生的感性经验，很多学生都看过大海，借助海天交界线、地平线的图片，帮助学生唤起感性认识。另一方面，播放古人对海天交界线、地平线的认知：古人认为天圆地方，并在绘画中用一条贯穿画面的线表示海天交界线和地平线。通过这样的方法，帮助学生形象的认识直线，并为进一步抽取直线的本质特征做准备。使用这个素材，还有一个好处，就是帮助学生理解海平线、地平线并非直线本身，激光笔射出的光线、拉直的毛线也并非射线、线段本身。学生能更容易地区分什么是数学中的线段、射线、直线，什么是线段、射线、直线的表达方式。

二、运用几何原型，需要从多方面着手，破立融合

教师依次展示三组生活中的图片，让学生分别表示出看到的共同的线。

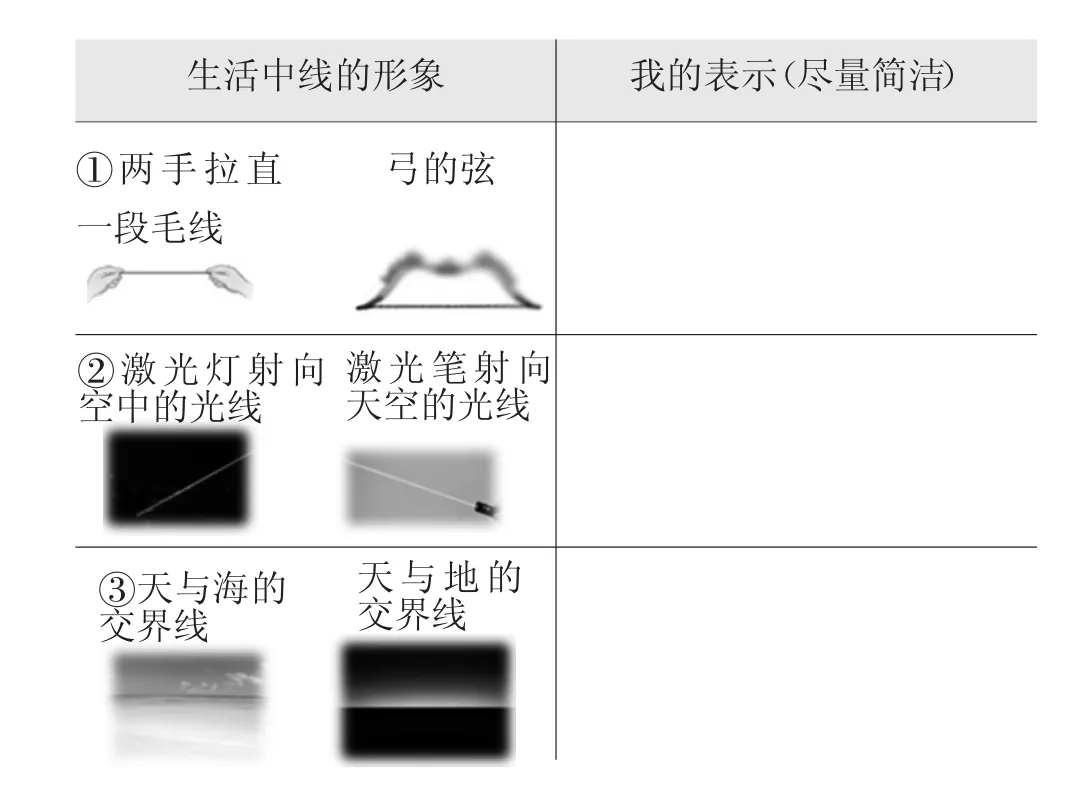
生活中线的形象我的表示（尽量简洁）①两手拉直一段毛线弓的弦②激光灯射向空中的光线激光笔射向天空的光线③天与海的交界线天与地的交界线

（一） 学生独立画一画、写一写

教师巡视的过程中用红笔在作品旁边进行编号。请学生小组交流，说说自己为什么这样画。在交流过程中，教师请A、B、C三组汇报的学生做好发言准备。

抽象需要建立在一组原型的基础上，在这里，每一组至少要给出两组原型。同时要给学生充足的时间进行独立思考和操作。把按几何图形抽象程度的不同从低层次的抽象到高层次的抽象编写序号，例如A①A②……这样在进行介绍时，材料的呈现就是有序的。

（二） 全班交流

按照顺序，分别交流自己画出的线是什么，并说一说自己为什么这么画。

（A组学生用的笔是粗细不同的，有水彩笔，也有铅笔。）

生：我画的是线段，这里是线段的端点。

师：（追问） 同学们用的笔颜色不一样，粗细也不一样，但为什么画出来的都是线段呢？

生：因为都有两个端点，直的。

师：线段能量出长短吗？

生1：能，因为有两个端点。

师：线段可以无限延伸吗？

生：不能，因为再长的线段，只要有端点就截止了，不能无限延伸下去。

师：同学们能用动作或手势表示线段吗？

（学生用各种动作和手势表示线段。）

师：掌声送回A组同学。

（A组回的同时，B组上台展示。B组学生按照次序展示自己的作品，并说说自己为什么这样画。）

生1：（画了一个点表示激光笔，并画了一束光，旁边标注：无限长） 这个点就是激光笔，这束光就是激光。

师：还能再简洁一些吗？

（生1没想出来，教师请生2展示。生2画一条射线，画到纸的边沿。）

生2：我觉得可以画到纸的边，因为激光可以射到很远的地方。

（学生们表示同意）

师：（追问） 画到纸的尽头了，你想表达什么？

生2：还可以继续画下去。

师：你能比划一下吗？

（生2继续比划，划出课桌）

生：还可以画出教室，画出地球，画出宇宙。

生3：（画了一条射线，旁边写了无限长） 我虽然画的很短，但是它是无限长的。

师：（追问） 不写字，能看出无限长吗？

生：能！只要不画另一个端点就行了。

师：这样的线，给它起个什么名字呢？

生：射线。

师：同学们能用动作或手势表示射线吗？

（有的学生放平胳膊，用一端握拳，一端放平来表示射线。也有的学生用手指指向天空来表示射。请B组回的同时让C组有序地摆。C组画之前教师再次展示大海的PPT大图。）

生：哇！真美啊！

师：这条海天交界线，大家也画出来了，一起来欣赏吧。

生1：（画的直线到了纸的边沿） 这是我画的线，我觉得海天交界线和地平线都是直的，没有边际的，所以我用一条直的线来表示。

生2：（画出一条直线，标注无限长）我觉得一张纸是画不下的，所以我没有画满，标注了无限长。

师：如果让你继续画你会怎么做？

生2：继续向纸的外面画，还可以继续画，画出教室，画出中国，还能画出宇宙呢！可是没有那么大的纸。

师：你这辈子能画完吗？

生2：画不完，无穷无尽的。

生3：（画出一条线段，并将两端延伸）我觉得直线就是把线段延伸得到的，只要不给直线的两端点上端点，就能表示一直延伸下去。

师：问下面的同学，你们有什么问题吗？

生4：我画的是一条线段，因为我觉得大海是有边界的，大地也是有边界的。

师：你的知识可真丰富，你猜古人知道大海和大地是有边界的吗？

生4：不知道，古人认为天圆地方，大地是没有尽头的。

师：古人看到大海的时候，心中也是发出了这样的感慨，所以就想表示出这种一望无际感觉，如果画下来，你猜会怎么做？

生4：如果我是古人，我画一条直的线来表示，不会给它点上端点。

师：你是个有思想的学生，不仅能认识到自然界大海是有边际的，又能想到可以这样表示无边无际的感觉。

师：这样的线，你叫它什么线？

生：直线。

师：谁能用手势比划一下直线？

（学生用各种方法比划直线，有的把手臂伸平，有的用指尖像两端指……）

在学习这节课时，很多学生都知道了射线、直线的名称，但对于射线、直线的本质，认识并不深刻。在这个环节，学生先复习线段的相关知识，唤醒对线段认识的经验，并借助已有经验进一步认识射线和直线。调动学生多感官观察、体验、思考线段、射线、直线的本质特征，学生就会更容易理解线段、射线、直线没有颜色、粗细，它们都是抽象的。在教学直线的过程中，处理好直线的原型很重要，应把生4的画法放在最后展示，这样不仅不会影响学生对直线的抽象过程，避免前摄抑制，还能顺利向下个环节过渡，引出对原型、模型的对比思考。

（三） 区别原型与模型，从几何本质认识线段、射线、直线

师：由于科学技术的发展，我们知道大海、大地都是有边界的，那么海平线、地平线是直线本身吗？

生：不是。

师：那么激光笔射出的光线是射线本身吗？

生1：我认为是的，因为激光笔射出的光线是无限延伸的，可以射到宇宙中去。

生2：不是，因为激光笔的光柱有粗细，而且也不能无限延伸下去，因为会没电。

（学生掌声表示同意）

师：那么拉直的毛线是线段本身吗？

生：不是，因为毛线就算拉直了，上面也是不平的。

师：孩子们，你们真会思考。生活中这些事物，并不是线段、射线、直线本身。那么老师在黑板上画的线段、射线、直线是它们本身吗？

生：应该也不是，因为如果放大镜看，肯定不是直的。

师：如果我在黑板上画1米的直线，可能吗？

生：不对，因为直线不可能一米长，老师在黑板上画的，是直线的样子。

师：是的，黑板上所画的，是线段、射线、直线的一种表示方式。我们借助生活中的这些事物更好地理解线段、射线和直线，并用绘画、语言、手势来描述它们。

通过追问，让学生理解原型和模型的关系，进一步区别原型和模型。

（四） 感受三线的关系

师：（指着黑板上的名称） 它们看起来很像，却又不一样，你能说清楚它们的相同点和不同点吗？（让学生小组内说一说。教师巡视，请最先完成的组汇报。）

生1：它们的共同点是，都是直的。

生2：不同点是，线段有2个端点，射线有1个端点，直线没有端点。

生3：我来补充，线段是有限长的，射线和直线都是无限长的。

生4：我还发现，把线段一端延长，就得到一条直线，把射线反向延长就得到一条直线，射线和直线上都能截取出线段。

让学生在观察思考中理解三线之间的内在联系，深化对线段、射线、直线的认识。

（五） 展示平面几何学产生的历史

师：（展示一列生活中的线，再展示一列数学中的线） 这是我们得到线段、射线、直线的过程，谁能总结一下数学中的这些线，是怎么得到的？

生：从生活中得到的。

师：是呀，数学就是源于生活，由高于生活的，它因人类的好奇，表达的需要而产生，是我们对世界高度抽象、概括的结果。（微视频播放几何学产生的历史。）

早在五千多年前的古埃及和古巴比伦，人们在祭祀、生产、生活中想用简洁的符号表示自己看到的和想到的，就有了最初的线和图形，有了数学图形这门“语言”，人类在表述时，就变得非常简洁。

从原型到模型的几何抽象过程易于被学生接受，通过层层追问，让学生进一步理解原型并非模型本身，了解数学原型都有其产生和发展的历史，从而培养学生的数学思维能力和对数学的兴趣。

（作者单位：江苏省南京市孝陵卫中心小学）

（责任编辑：杨强）