小学数学教学中形成性考试的编制和结果分析

◎陈为强

小学数学教学中形成性考试的编制和结果分析

◎陈为强

一个完整的教学过程要历经教学设计、教学实施和教学评价三个主要阶段。可见，教学评价在教学活动中是非常重要的，它起着鉴定、调节和监督的功能。考试是教学评价中常用的办法。通常我们都是从教育测量的角度出发，把考试作为一种对学生成绩测量的手段，重视考试结果的分数和对分数数据的处理。而往往忽略了考试作为教学过程的一个组成部分，其本身具有诊断、导向功能。

一、应当明确区分的两种考试

考试是教学中最常见的评价方式。考试分为选拔性考试、形成性考试、诊断性考试和总结性考试。教育测量中称前一种为常模参照性测验，后三种为目标参照性测验。其中选拔性考试用于把学生分类、排队，它注重考试结果的量化——分数或等级，按照分数或等级把考生分类。因此，它的命题追求考试分数和等级的正态分布，以达到把考生分类排队的目的。而教师在教学中常用于教学评价的课堂测验、单元测验、阶段性测验都是形成性考试，它是一种目标参照性测验。形成性考试的命题不追求考试结果的正态分布，只考察学生的学习是否达到了教学目标的要求，它的结果只有达标和未达标两种。所以，形成性考试主要不是用来表现学生成绩好差序列的，而是用来表现学生学习状态的。

形成性考试不只是一种测量，它更是一个过程。它是一个获取教学和学习状态信息、分析教学和学习信息、实现反馈调整的过程，这个过程是通过学生考试和对考试结果的分析完成的。学生在回答试卷的过程中表现出他对所学习知识了解的状况，折射出其能力发展水平，反映出教学目标达成度的状况。形成性考试的试卷不是随意编辑的，它应当符合下面两个条件：它所要考察的知识和能力是教学要求的有代表性的样本，学生对试卷的回答能在一定程度上反映出教学目标达成度。

二、形成性考试试卷的编制

形成性考试试卷命题的总体思想是：立足教材基础，体现数学本质，注重思维品质，关注学生差异。在确保立足知识的基础上，还要兼顾“知识立意”和“能力立意”的完美结合。因此，形成性考试是一个为教学服务、目的非常明确的考试，它不是可以随意编排的考试。那么，我们应当怎样编制形成性考试试卷呢？

（一） 形成性考试试卷编制的要点

形成性考试试卷编制前，教师必须弄明白这次考试为什么考、考什么、考什么人、怎样考。形成性考试的目的是非常明确的，那就是为了了解教师的教学和学生的学习状况，改进教师的教学和学生的学习；考什么就是要决定考试的范围和内容，目的是通过这次考试可以比较准确地了解到所考的阶段教学和学习的基本状态；考什么人则是决定考哪些学生，他们的基本情况怎么样；怎样考是这次考试的形式。

试卷测验应能明确界定学生能否达到教学目标。教学目标的确定主要是教材规定的知识和能力。所以编制试卷的首要工作不在于编出试题，而是要认真研读课标和教材，使编制的题目更能有的放矢。

试卷的各项试题应能测量出预期的学习结果，能比较清楚地显示出学生学习的成功与不足。因此，教师在确定考试内容之后，编制试题之前，应先列出一个试卷试题的细目表。这个细目表应反映出教学内容、教学目标与试题的对应关系，利用这个细目表可以使我们明确地规划好要检测哪些学习内容和能力，而不会使教学目标漏测。在这个表中还可以按照教学内容和教学目标的相对重要性，给出在试卷中所占的不同比重，成为检测不同内容和不同能力试题所占分数的依据。在细目表的指导下选择试题类型，并编制试题。

（二） 细目表的编制

编制形成性考试试卷细目表首先要了解细目表的结构。细目表的横向是教学目标，它应当是所要考的知识和能力、过程和方法、情感态度和价值观三个维度的内容。形成性考试所测的重点是以知识、能力和方法维度为主，所以细目表横向表现的是能力、方法或者数学思想。细目表的竖向是学习内容，它是这次所要考的知识。表中所要填写的是由表的横向和竖向项目所决定的这一内容在试卷中所占的分值（一份试卷总分值，例如可定为100分） 和预计的题号，分值表示了这项内容在试卷中的权重，显示出这一内容在这一段学习中的重要程度。例如一份六年级数学课程“圆柱和圆锥”单元检测试卷细目表如表1所示：

（注：表中数字为该项所占的分数，括号中是该项在试卷中的大题号和小题号。）

有了这个细目表后，教师要按照教学要求对各项分数值进行调整，使得这份试卷具有代表性，符合考试要求。这个细目表实际上是试卷的总体设计方案，是编制试卷的思维导图，为试卷的编制奠定了基础。

（三） 试卷的形成

试题的种类有许多种，按形式来分，可以分为选择题、判断题、搭配题、计算题、填空题和问答题、推理证明题等。如按评价方式来分，前五种称客观性试题，其评价结果一般不受学生主观及环境因素左右。后两种称主观性试题，这类题目的回答能够反映学生的问题解决策略和方法，反映出背后的数学思想以及学生的思维水平。在编制试题时应依据细目表中试题的内容、学习结果和分值编制出试题，由于试题的种类繁多、形式各异、功能不同，所以要依据细目表中的内容、学习结果和分值来选择恰当的试题形式，组成检测试卷。

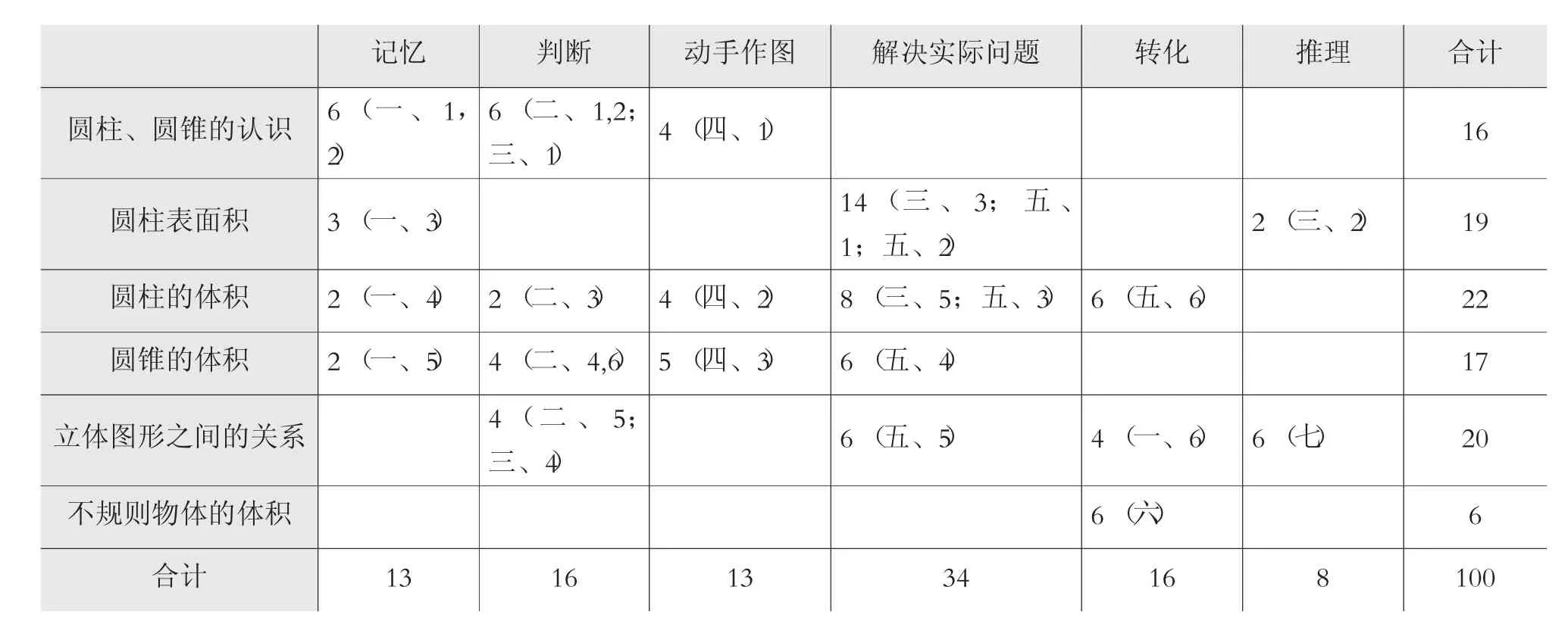
表1

三、形成性考试结果的分析

形成性考试结束后，传统的做法中教师最关心的是每个学生的分数和全班的平均分数，把学生按分数排队，用全班的平均分和其他班比较，这实际上是一种选拔性考试的分析方法，对教师的教学改进意义并不大。因为这种分析方法只关注学生的等级、名次，并不关注每个学生学会了什么，没有学会什么。例如两个成绩都是88分的学生，我们往往把他们看成学习情况是一样的，但是他们会哪些、不会哪些可能是完全不同的。因此，为了有效地改进教学和帮助每一位学生，教师在每一次形成性考试后不能只看分数，应当通过对试卷的分析，了解某一个学生或者全班学生总体的学习状态。下面通过具体实例来说明形成性考试结果的分析方法和步骤。

某校小学六年级学过“圆柱和圆锥”一章后进行了检查教学成果的形成性考试，其命题的细目表如表1所列。

（一） 直观地反映学生的个人学习状态

这次考试某个学生答题得分如表2所示：

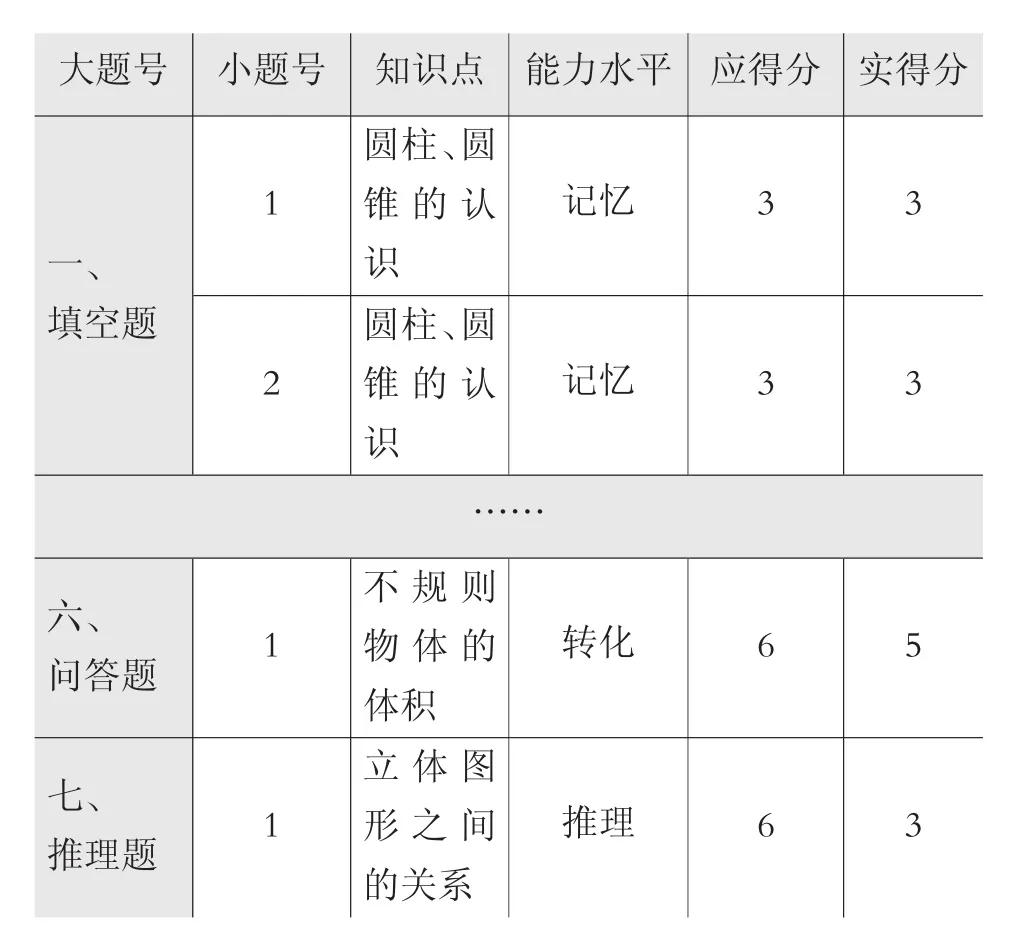
表2

我们可以从这个得分表中算出各个知识点和各个能力水平发展的得分率，并列出下面两个表3和表4。

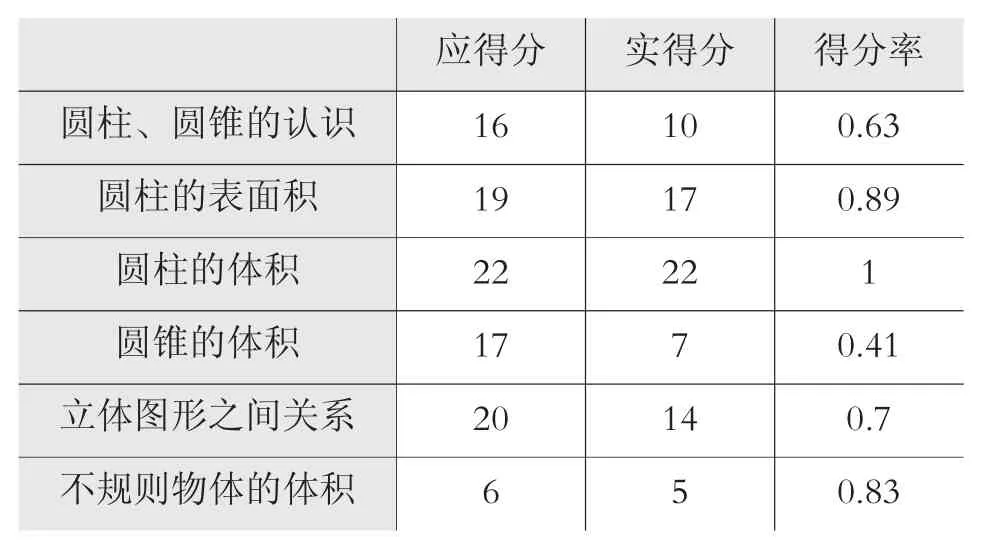
表3

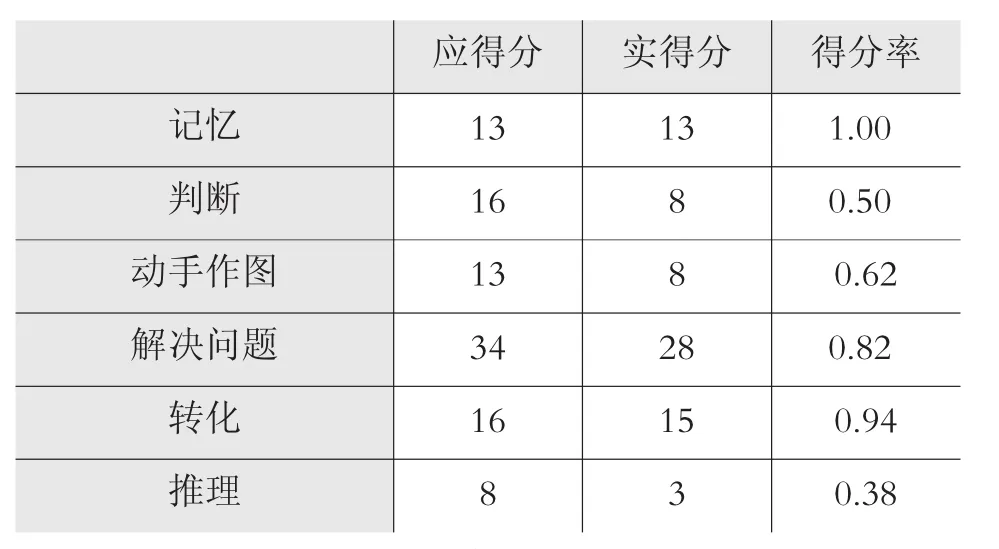
表4

由表3、表4可以画出相应的得分率条形统计图:图1、图2。

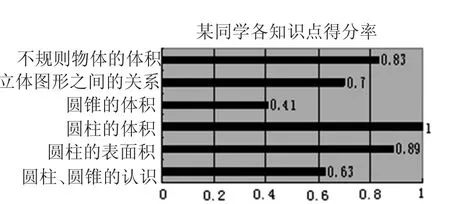
图1

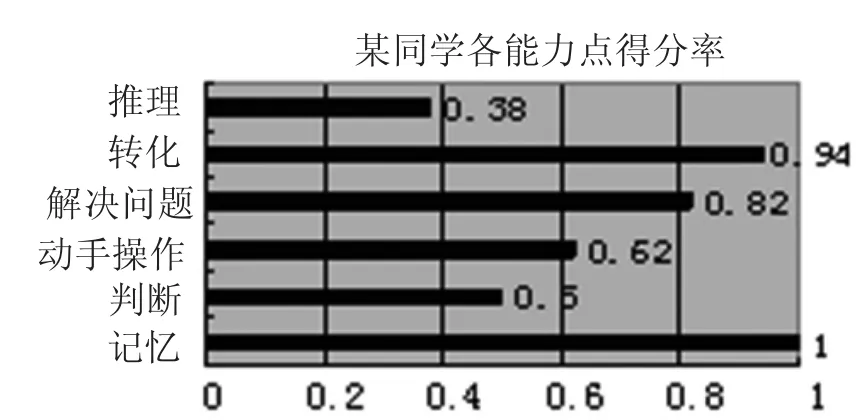
图2

从表3和图1可以看出，这位学生对于圆锥的体积掌握得不好，第二题的第2、4、6题和第五题的第4题均全部出错，第四题的1、3两题也出现不同程度的错误，反映出该生没有真正理解圆锥体积公式的推导过程以及对于圆锥的认知还存在误区，表现在不能结合实际解决相应的问题。但是对于圆锥体的字母表征能够正确的表达，这说明这位学生对圆锥的学习仅停留在记忆层次上，不能灵活运用公式解决相应的问题。从表4和图2可以看出，这位学生的判断、动手操作以及推理等能力较差，大部分属于判断的题型回答得不好。这当然与没有真正地理解圆锥体积公式的推导过程以及对于圆锥的认识不完善有着密切的关系，由于不理解，就不能正确、合理的判断。该生在几何图形的读图、理解图和图形之间的转化的方面较弱，所以表现出动手作图能力较弱。推理能力弱的主要原因是教师在平时教学中重视了陈述性知识和程序性知识的教学，而忽视了类比能力、归纳能力等策略性知识的培养。这些分析可以使教师对这个学生这一阶段的学习状况有一个较为清晰地了解。当然，针对学生个别出现的具体问题，教师可以设计出更加细致的诊断性测验来进一步确定问题的具体所在。当我们把表和图提供给学生时，学生可以很容易地判定自己的学习状况，也会对自己下一步的学习作出判断和调整。通过这些表和图引导学生反思，起到用考试促进学生学习和发展的作用。教师也可以从这些表和图中了解这位学生的学习状况，更好地为他提供个别辅导。

（二） 可视化分析全班学生的发展状况

借助计算机得到这次考试全班各题总得分情况：（如表5）

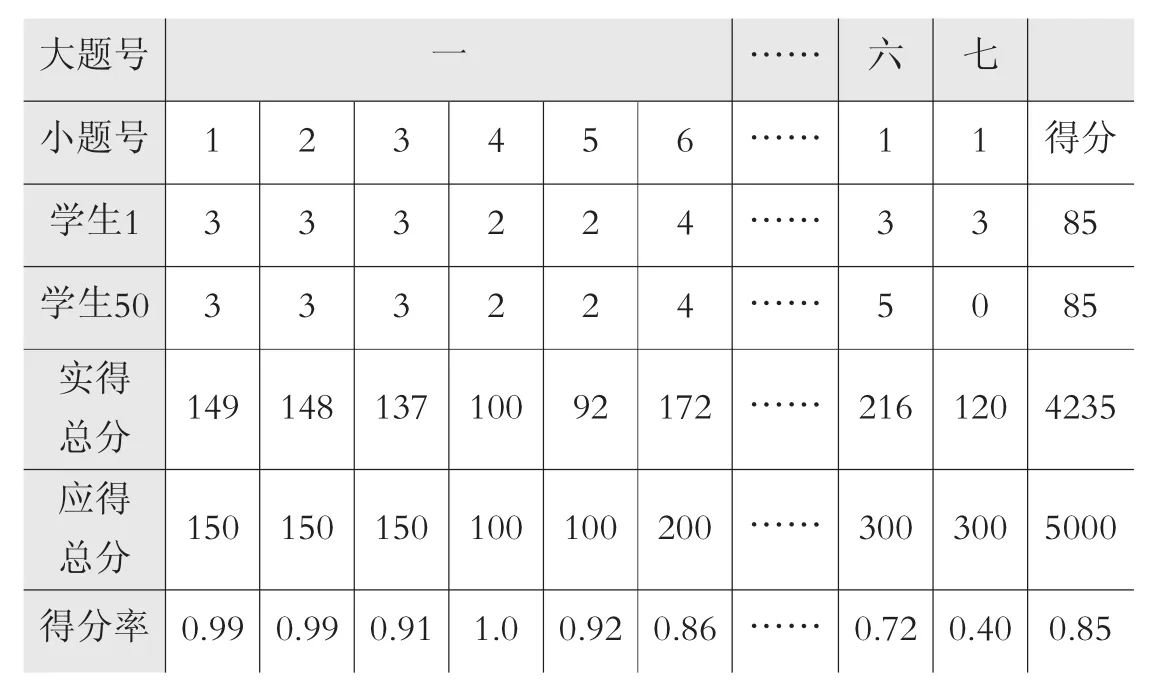
表5

根据这个得分表列出各知识点和能力水平的得分率后，分别绘制成知识和能力统计图如图3和图4所示：

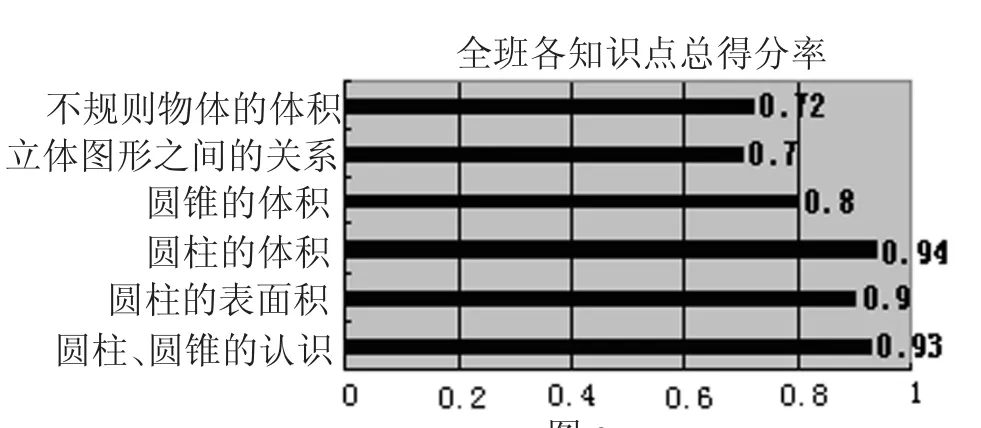
图3

图4

从这些利用大数据制成的条形统计图中可以直观地看出，这个班在这单元的学习中属于中等水平，就各知识点来说，学生们掌握得还可以，只是在圆锥的体积、几种立体图形之间的关系和不规则物体的体积等方面掌握得稍微弱一些。从能力水平来看，最弱的是推理能力，其次是动手作图能力和转化能力。这说明学生对于知识的记忆和直接运用公式解决简单的实际问题做的较好，而对于概念的本质理解和灵活应用则学得不好，主要体现在推理能力和转化能力较弱。这些图还反映出学生作图能力较弱，实物和空间想象后的抽象图不能互换，表现出学生动手实践较少。分析在教学中动手操作时，一个小组往往只有少数学生动手，多数学生只充当“看客”。这就造成了很多学生动手能力弱，忽略了操作经验的提升和内化，这些方面都是以后教学要改进的。

还有，在教学中教师没有从联系的角度沟通知识之间的关系，造成学生知识是碎片化、零散的，出现“只见树木、不见森林”的局面，不能综合灵活地解决问题。教师在以后的教学中，设计练习时要注意与根本呼应，注重核心内容的落实；与整体相连，注重知识的沟通；与思想结合，注重思想方法的孕伏。在设计综合题目时，要打破章、块的界限，以题目的相对难度取代综合题目的绝对难度，让学生的知识形成系统，训练学生的“综合性地思考”，提升学生的数学核心素养。

（作者单位：江苏省徐州市贾汪区实验小学）

（责任编辑：杨强）

本文系江苏省教育厅基于测试分析的跟进式改革重大研究项目“基于小学数学学科测试分析的教学实践研究”阶段性研究成果，课题编号：2015JYKTZD-09。