论卡西尼曲线与无限长均匀带电直线系统等势线的关系

姜付锦 吴 珊

(武汉市黄陂区第一中学 湖北 武汉 430300)

论卡西尼曲线与无限长均匀带电直线系统等势线的关系

姜付锦 吴 珊

(武汉市黄陂区第一中学 湖北 武汉 430300)

通过对卡西尼曲线和伯努利双纽线一般形式的研究得到了其基本的几何性质，由此猜想了广义的卡西尼曲线和广义的卡西尼曲线簇，并用Maple13对其进行了数值模拟.接着推导出了无限长均匀带电直线系统等势线方程，发现其等势线方程与广义的卡西尼曲线簇具有相同的形式，从而证明了广义的卡西尼曲线簇就是无限长均匀带电直线系统等势线.

卡西尼曲线 无限长均匀带电直线系统 等势线

1 卡西尼卵形线和伯努利双纽线简介

卡西尼卵形线是这样的曲线：设点M到两个定点F1与F2的距离的乘积是个常量，即

MF1·MF2=b2

式中b是一个常数.点M的几何轨迹叫做卡西尼卵形线[1].

设F1F2=2a，取F1F2所在直线为极轴，线段F1F2的中点O为极点，则可推导出卵形线的极坐标方程为

两种情况的图形如图1所示，第一种情形对应一条封闭的曲线，第二种情形对应于两个分开的封闭曲线，而当a2=b2时，所对应的曲线即伯努利双纽线(图2)[1]，所对应的方程为

r2=a2cos 2θ

图1 a2b2卵形线

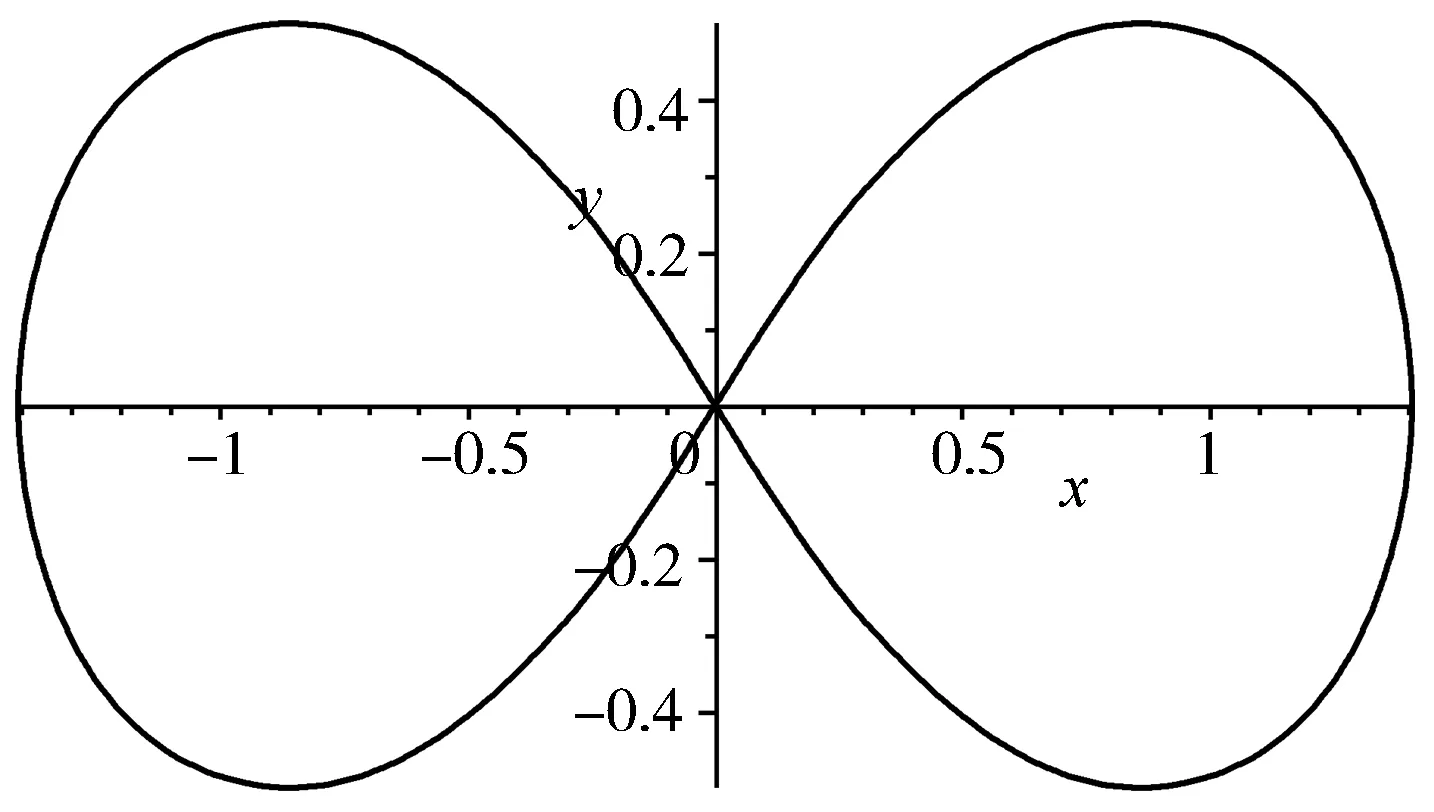
图2 伯努利双纽线

对于卵形线和双纽线，还有下列性质[2]：

(1)当a2b2时，r的最大值和最小值分别为

(2)当b2≥2a2，曲线是一条凸曲线.

(3)当b2=0时，曲线退化为2个点，即F1和F2.

2 广义的卡西尼曲线

设F1，F2，F3,…,FN是平面内N个定点，点M到F1，F2，F3,…,FN的距离满足以下等式

MF1τ1·MF2τ2·…·MFNτN=bN

点M的轨迹就是广义上的卡西尼曲线，式中τ1,τ2,…,τN为一系列的实数，b,N为两个实数.

若N=2,b变化时，则会得到一个卡西尼曲线簇，如图3和图4所示.由图可知,它们开始是分离的两个卵形曲线，后来会变成一个完整的曲线；若τ1,τ2,…,τN的正负相同，则会有伯努利双纽线；若τ1,τ2,…,τN正负不同，不会形成伯努利双纽线.

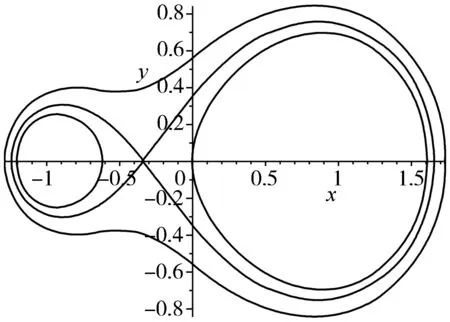
图3 广义的卡西尼曲线簇τ1=2,τ2=1

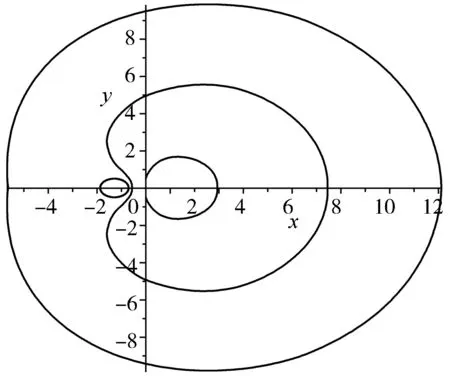
图4 广义的卡西尼曲线簇τ1=2,τ2=-1

3 无限长均匀带电直线系统形成的等势线

若能求出一根无限长均匀带电直线的等势线方程，再利用电势的叠加原理就可以得出多根无限长均匀带电直线的等势线方程.

3．1 一根无限长均匀带电直线产生的电势[3]

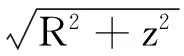
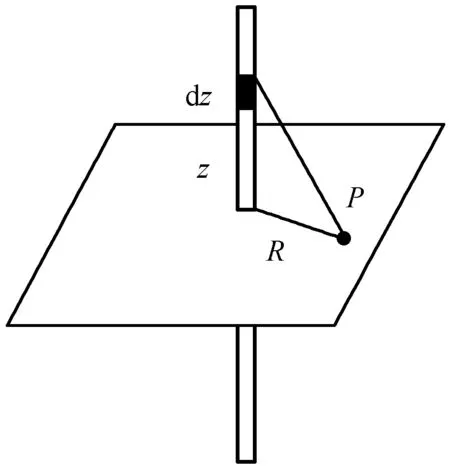
图5 均匀带电无限长直线的电势

积分结果是无穷大，无穷大的出现与电荷不是有限区域内的分布有关.计算两点P与P0的电势差可以不出现无穷大.设P0点与导线的垂直距离为R0，则P点与P0点的电势差为

若选P0为参考点，规定φ(P0)=0，则

3.2 两根无限长均匀带电直线形成的等势线方程

如果平面上有两根无限长带电直线，则某点M的电势可以写成

式中τ1,τ2分别为两根无限长带电直线电荷的线密度，F1,F2分别为两根无限长带电直线的中心点，P0为参考点，规定φ(R0)=0[4].

若设

则可以化简为

MF1τ1·MF2τ2=R0τ1+τ2e-2πε0C

若令R0τ1+τ2e-2πε0C=b2，则可变为广义的卡西尼曲线的一般形式

MF1τ1·MF2τ2·…·MFNτN=bN

当式中b取不同的数值时就会得到广义的卡西尼曲线簇，如图6所示.

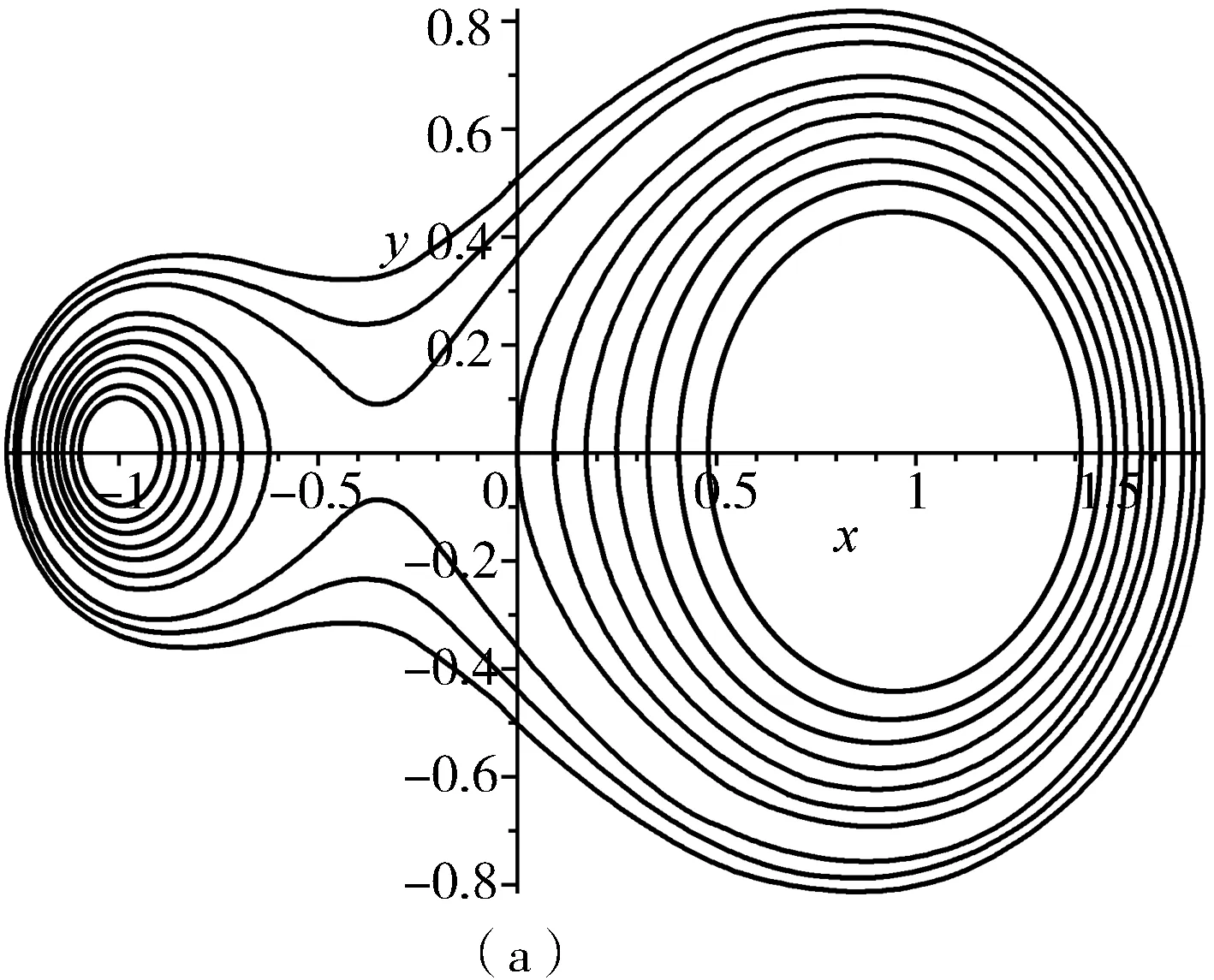
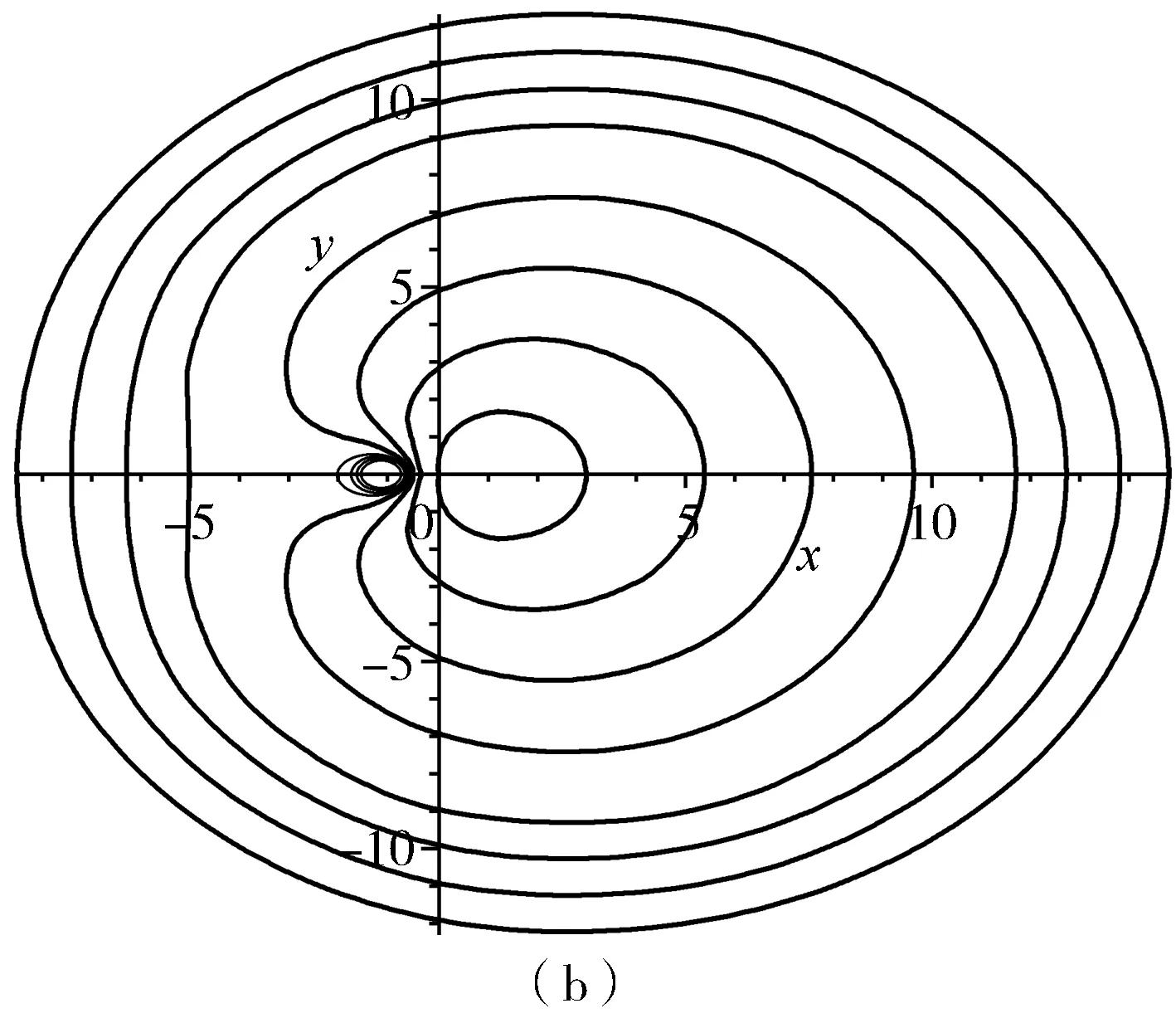
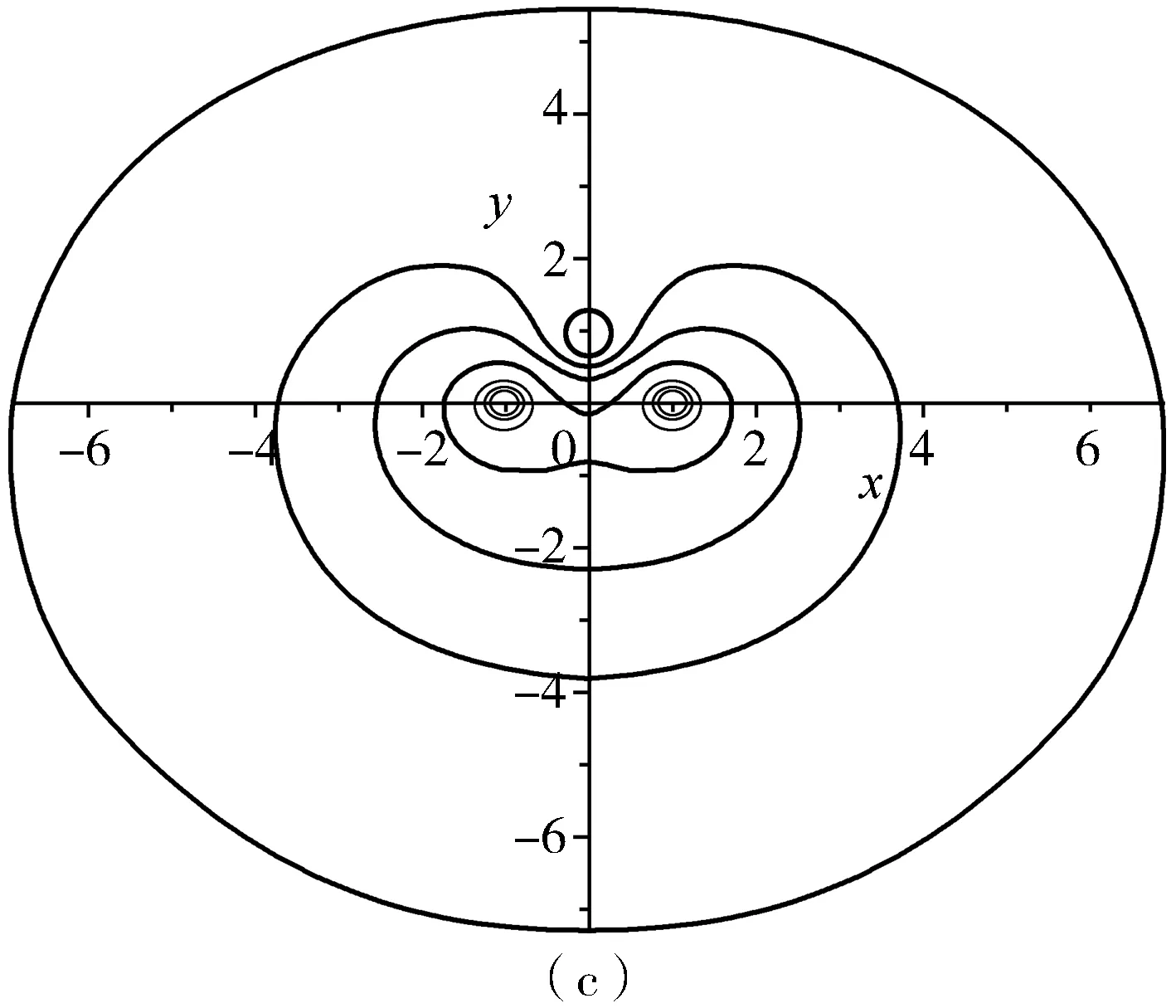
图6 广义的卡西尼曲线簇

4 结束语

广义的卡西尼曲线簇在本质上是无限长均匀带电直线系统形成的等势线，其中卵的中心就是每根带电直线的中心，若这些中心某几个可以包裹在一个封闭的曲线里，则说明它们带电的性质相同；若开始相互隔开的，则它们的电性相反；若某几个中心开始是隔开的最后在更远距离上包裹在一个封闭的曲线里，则说明后来被包裹的那个直线的电荷量小于包裹它的那几根直线的总电荷量.无限长均匀带电直线系统的等势线还可以利用莫尔条纹来分析[4]，限于篇幅这里不再赘述.

1 B·H·斯米尔诺夫著.高等数学教程.孙念增,译.北京：商务印书馆，1956.200～201

2 王叙贵.多卵线与多纽线——卡西尼卵形线与伯努利双纽线的推广.昆明师范高等专科学校学报,2001，23(4)：34～36

3 郭硕鸿.电动力学.北京：高等教育出版社，2012.37～43

4 李治林，刘建科．利用莫尔条纹模拟叠加静电场的等势线．大学物理，2011(6):47～51

2016-12-16)