论Mathematica在高中物理教学中的应用原则*

陈 星

(无锡市第一中学 江苏 无锡 214031)

论Mathematica在高中物理教学中的应用原则*

陈 星

(无锡市第一中学 江苏 无锡 214031)

通过实例展示了科研用数学软件Mathematica在高中物理教学中辅助处理较难数学问题时带来的巨大便利.具体探讨了在解方程、难题的结果演示、数据拟合、画图等方面的应用.

Mathematica 高中物理 应用原则

高中物理教学经常会遇到复杂或者棘手的数学问题，而当学生基本能力训练已经满足，但通过现已掌握的技术和能力很难做出时，若适时借助数学软件Mathematica[1,2]则可以很快捷而形象地将该问题的解决方案展示出来，为教师的教和学生的学都大大节约了时间，又能很直观地给学生留下深刻印象.通过实践研究，高中物理教学中以下几种情况比较适合应用Mathematica.

1 解方程

高中阶段学生应掌握的基本解方程组能力包括3～4个简单方程组，若超过4个或者较复杂的方程组则其实已经超出基本能力的要求，过多纠结于此对物理教学反而是一种拖累，这时可以考虑使用Mathematica.除方程组外，有时可能还会遇到初等数学根本就解不出来的简单方程，这时也可借助Mathematica.

1.1 多方程组方程

如图1所示，轮轴重量为G0，半径为R，轮轴上鼓轮半径为r，轮轴靠在水平面和竖直墙壁构成的墙角处.在鼓轮上缠绕轻质绳，经过光滑的定滑轮在绳的另一端系一重物，轮轴与墙和水平面间的动摩擦因数均为μ，拉轮轴的绳与竖直方向夹角θ已知.求平衡时重物的最大重力Gx.

通过受力分析(设地面支持力为N1，摩擦力为f1，墙面支持力为N2，摩擦力为f2)，对本题可列出力平衡方程和力矩平衡方程

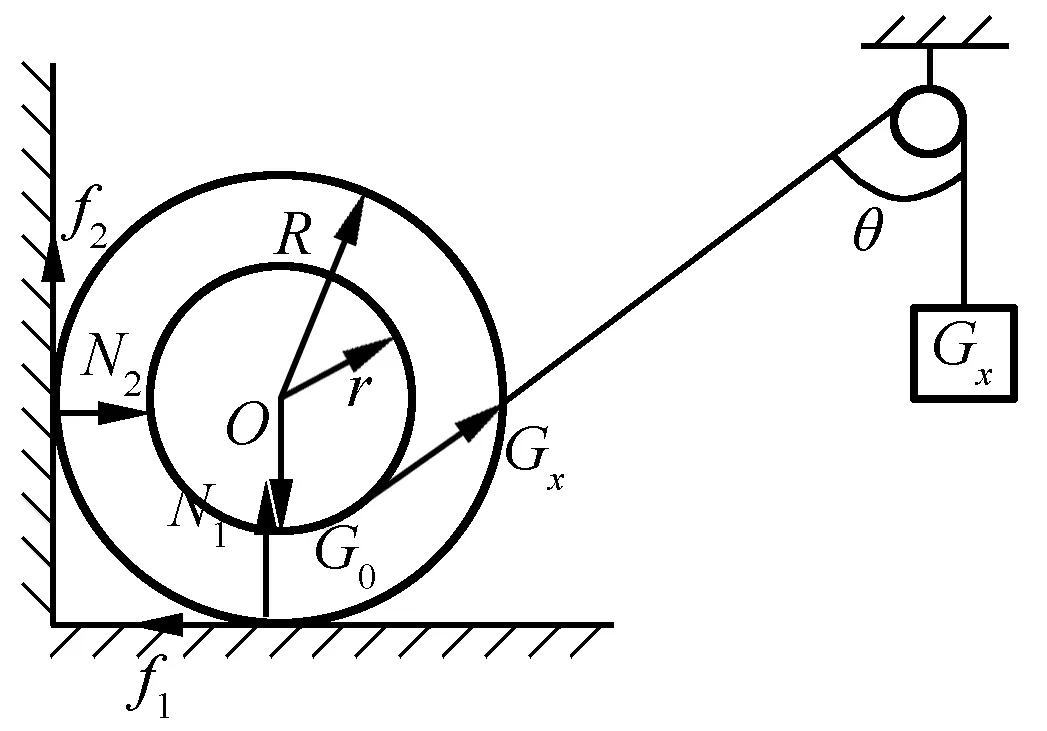
图1 平衡时的轮轴连接装置

手工求解以上方程组非常繁杂，但在Mathem-

atica中只需键入以下程序：

Solve[{Gx*Sin[θ]+N2-f1==0,Gx*Cos[θ]+N1+f2-G0==0,Gx*r-(f1+f2)R==0,f1-μ*N1==0,f2-μ*N2==0},{Gx,N1,N2,f1,f2}]

运行，可立即得到：

对该结果化简：

1.2 图解法

有一个弹簧振子质量为m，放在光滑水平面上如图2所示，平衡位置为O点，其圆频率为0.5π/s.另一个质量也是m的滑块由h=0.20m高的A点由静止滑下，质点滑到曲面底部B需时tAB=1.5s，OB间距l=6.0m.现将弹簧振子向左压缩到x0=2.0m处时开始计时，两个物体同时释放，求：释放后多久二者相碰.(不计摩擦)

图2 一个物块释放撞击另一个连接弹簧的物块

对物块1由简谐振动，对物块2考虑动能定理并从B开始匀速运动有

2(t-1.5)-2cos0.5πt=6

该方程形式虽简单，但凭借高中数学知识，手工求解此方程难度很大，甚至是不可能.为此，可以把该方程拆分成两部分

在Mahtmatica中画出这两个独立的x-t图如图3：

Plot[{2Cos[1.57t],2t-9},{t,0,6}]

则二者交点就应为方程的解.为此，运行：

FindRoot[2Cos[1.57t]==2t-9,{t,5}]

立即得到上面方程的解：

{t→4.80507}

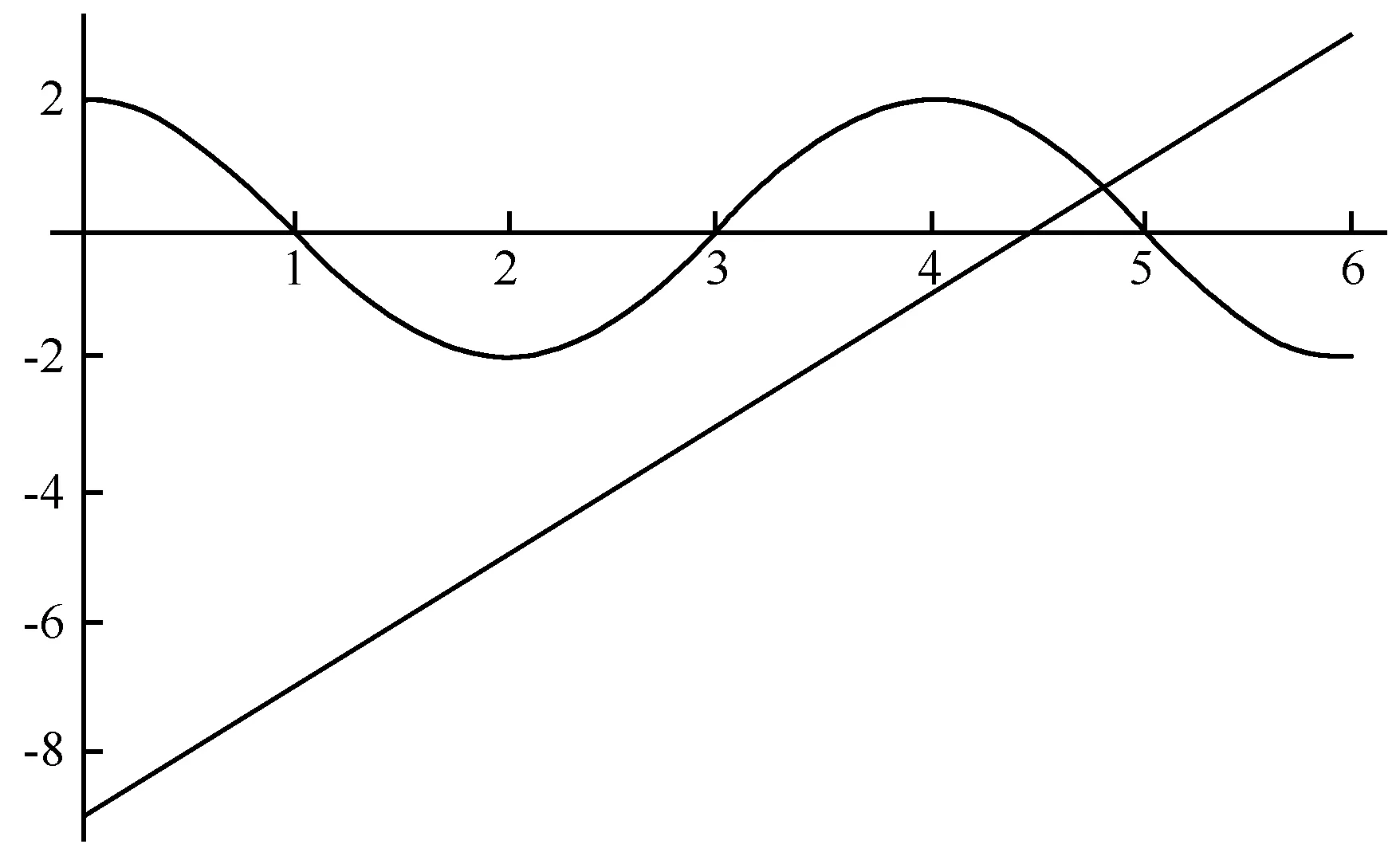
图3 x1-t和x2-t的函数图像

2 难题的结果演示

有些问题求解完成后，其结论函数很复杂，若要求探究其结论值随各个变量的变化关系，或者要求找到结论函数极值及其位置，但初等函数知识很难求出时可以使用Mahematica.

2.1 复杂结论函数三维图展示

承接1.2中的例子，若物块1质量为M，弹簧劲度系数为κ，试探求物块1从开始运动算起的位移x随时间t和物块2质量m之间的变化情况.

为方便起见，取M=50 kg，κ=50 N/m，g=10 m/s2.碰撞后，对M和m组成的整体由简谐振动有

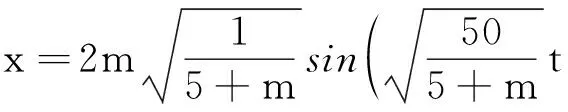
显然，单纯的分离变量法很难看出x随m的变化关系，且t不同时，x随m的变化情况也会受影响，为此可以画出x随t和m变化的三维图像如图4所示：

图4 位移随时间和质量的变化

由图可看出x随t做标准的正弦曲线变化，而当t相同时，x随m也做一定的波动性变化，且t不同时，这个波动的“周期性”不同.可想而知，若不借助三维图，是很难看出来的.此外，为方便看出变化关系，还可以从不同角度看这个三维图，只需键入以下命令：Show[%,ViewPoint→{1,0,1.2}，就可从该图的右上方如图5所示清晰看出x随m的波动性变化.

2.2 求函数极值

一条轻质绳子长度为L，一端固定在O点，另一端栓一个质量为m的小球，拉起小球使轻绳处于水平，然后无初速度释放小球，如图6所示，则小球所受重力的瞬时功率在何处取得最大值，最大值为多少？

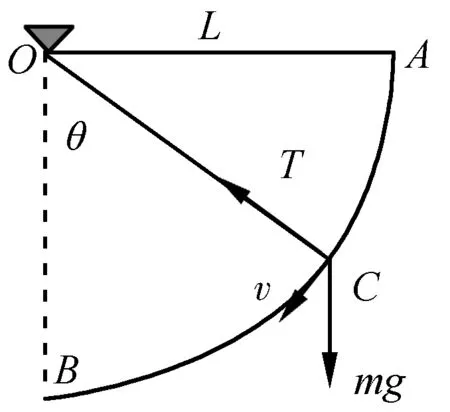
图6 静止释放的小球

对小球由动能定理和瞬时功率公式，有

即需要探求x-x3的极值.这种函数极值需要学过微积分后求导获得，高中课堂上直接求，显然不适宜.为此，借助Mathematica输入：f[x_]=x-x3；Plot[f[x],{x,-2,2}]先得到该函数曲线如图7所示.

图7 x-x3函数图像

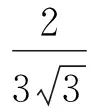
3 实验数据的拟合与处理

描点画图是学生高中阶段应掌握的基本实验技能.但若要求使用所测数据精确求解物理量或者拟合曲线方程时，应用手工绘制的图线则显然会因人而异且误差很大.这时，借助Mathematica则可以得到非常精确而一致的结果.

在“测电源电动势和内阻”的实验中，获得的一组电流、电压值如表1所示.

表1 测电源电动势和内阻实验的一组电压、电流值

要求根据所得数据较精确地求出电压随电流的变化曲线方程和电源电动势及内阻.在Mathemetica中先建立数据库：

S={{0.12,1.37},{0.20,1.29},{0.31,1.22},

{0.4,1.19},{0.5,1.12},{0.57,1.05}}

对数据拟合：nf=Fit[S,{1,x},x]，马上就可得到精确拟合函数：1.43682-0.65758x.即电源电动势为1.44 V，内阻为0.66 Ω.对数据进行描点，并把拟合函数画在同一副坐标中：tu1=ListPlot[S,PlotStyle→{PointSize[0.02]}];tu2=Plot[nf,{x,0,0.60}];Show[tu1,tu2],我们就可以在同一个坐标系内得到数据点和拟合函数图如图8所示.

图8 测电源电动势和内阻实验数据拟合

4 不易理论手绘的物理图景

有些物理图景很重要，但其方程形式却较为复杂，手工绘制几乎无法实现时，按照以往，教师只能以结论形式直接告诉学生，现在可以使用Mathematica在现场快速地绘制出来.

4.1 参数方程图线

一个刚性圆轮在直线轨道上做纯滚动，圆轮边缘上一点所经历的轨迹称为滚线(又称旋轮线、摆线).设圆轮半径R=0.5 m，向前匀速运动的速度v0=2 m/s，试探求该点的轨迹.

对该点由圆周运动和匀速直线运动不难列出其水平和竖直方向的位移随时间变化的参数方程

若力图整理出y随x的变化函数再绘图几乎是不可能的.这时就可借助Mathematica对x，y关于t进行参数方程绘图：

v0=2;R=0.5;

运行，即得摆线图像如图9所示.

图9 摆线轨迹

4.2 不等量同种电荷电场线

教材中的电场线是作为实验模拟后直接给出的.但事实上是可以从理论上绘出的.尤其是在处理非对称情形下的电场线时，重新做实验显然不现实，这时，又可借助Mathematica.例如，要求绘制两个不等量同种点电荷电场线(设其中一个带电荷量是另外一个的3倍).由高斯定理并结合点电荷场强公式，可以整理出多个共线点电荷的电场线方程为

把两个点电荷代入可得两点电荷空间电场线方程为

为定量画图，取q1=1，q2=3，a=1，可在Mathematica中输入：

ContourPlot[f,{x,-3,3},{y,-3,3},

ContourShading→None,

Contours→25,PlotPoints→100]

马上就可得到不等量同种电荷电场线如图10所示.

图10 不等量同种电荷的电场线

综上，凭借强大的符号、运算、绘图能力，Mathematica在高中物理教学中有着巨大的辅助潜力.在处理超出学生求解能力、又需要形象快捷展示物理图景的问题时都可以考虑使用.只要在此原则内，除所使用的例子外，在平时教学中只要肯动脑筋，一定能够挖掘出更多的场景配合以Mathematica的使用，为学习和教学带来更多的便利.

1 于凤梅, 王克强, 张麟. 运用Mathematica软件辅助大学物理教学. 现代教育技术与装备, 2011(15): 29～31

2 李寅杰, 徐慧. Mathematica软件在物理教学中的应用——以黑体辐射有关公式为例. 物理通报, 2015(12): 79～81

*中国教育学会教育科研规划课题“基于课程基地的CAP物理力学课程的教学创新研究”，项目编号：Z032016071

陈星(1982- )，男，中教一级，主要从事高中物理、物理竞赛、大学先修课等教学.

2016-11-23)