教育叙事：“两个密度”引发的思考

王宝柱

(太和县第一中学 安徽 阜阳 236600)

教育叙事：“两个密度”引发的思考

王宝柱

(太和县第一中学 安徽 阜阳 236600)

那是2016年的第一场雪，比以往时候来的更早更大一些，检查完早自习的我嫌回家吃饭有些浪费时间，干脆就在食堂对付一下，于是要了一碗稀饭和一份北方特有的葱油饼.我正吃到一半，就听见两个男生边吃饭边叽叽喳喳地在抬杠，离我桌子还比较近，真受不了，吃个饭也不消停.我正准备端碗挪走，其中一个学生用筷子比划的时候没在意，一筷子米饭粒扔到我鼻梁上面，我确实没忍住，一个喷嚏就送过去了，不愧是一中学子，两个家伙反应飞快，喷嚏没进入他们的势力范围.这时两个小伙子也算是知趣，忙跑过来又是给我擦脸又是满脸堆笑陪不是.俗话说得好，迎面不打笑脸人，何况我是谁啊，是老师，我平复了一下心情，深呼吸，摆出一副老师独有的架子——左手背后，右手前托：你两个熊孩子不吃饭在这里折腾啥呀！他俩有点不好意思，其中一个学生胆子大些(后来知道他认识我，是因为以前我上他班级听我们物理组老师的公开课)，从另一个学生后面挤过来，低声说：我们有个问题一直没弄明白，您是我们学校最厉害的物理老师，您就给我们说说吧.听到这么令人激动的话，再看到两个孩子那么上心地学习，一股暖流让我忘记了刚才的事情，内心里也确实为这两个孩子感到高兴，索性边一手拿着饼子，一手拿着他们的稿纸，题目可以概况为下面两个问题:

【例1】一未知天体,现测得其自转周期是T,问其平均密度满足什么条件,才能确保其不因自转而瓦解.

【例2】一未知天体,现测得其近地卫星的周期是T,问其平均密度是多少？

这两道题都是求密度，而且在条件上也有着惊人的相似：有周期，没半径.学生能发现这样的问题我感到很欣慰，我问题目是怎么发现的，学生说是他们自己在学习过程中从资料里发现并且整理出来的，拿出来讨论，还没来得及问老师.此时此刻，此情此景，能在食堂里给学生解决问题，实在是人生一大幸事，绝对能传为佳话.我拿出他们的笔，用着食堂里的广告纸，把过程给他们一一分析出，具体如下.

例1解析:这道题是属于天体运动中的临界值计算问题,由极限假设思想知,天体密度越大对外层物体的引力必然越大,就越不容易瓦解,显然我们应该求出最小密度,那么在什么情况下,所求密度最小呢？由向心力知识,只要赤道位置处的物体不因自转而被甩出即可.设未知天体质量为M,赤道位置处物体质量为m，天体半径为R,假设物体刚好未被甩出时的天体密度为ρ，由万有引力公式得

(1)

(2)

如果以地球为例,G=6.67×10-11N·m2/kg2，T=24 h=8.64×104s，代入解得

ρ=18.9 kg/m3

例2解析:设未知天体质量为M,近地面卫星的质量为m，天体半径为R,假设未知天体的平均密度为ρ0，由万有引力公式得

(3)

(4)

如果以地球为例,G=6.67×10-11N·m2/kg2，T=1.4 h=5 040 s，代入解得

ρ0=5.56×103kg/m3

解完以后，我为自己的表现十分满意，本以为两个学生能听懂，正准备庆功……结果两个孩子弄了半天没缓过神来，看着他俩木讷的表情，我也顿时懵了，大约僵持了25 s时间的沉默，其中一个学生终于忍不住了，问道：老师，分析上面的两个例子，我们发现一个现象，就是表达式几乎完全一样，但得到两个完全不一样的结果，这是什么原因呢.我定睛一看，确是如此，站在老师的角度，解题的过程自然是水到渠成，无可厚非，然而站在学生的角度却非如此，接下来我就静下心来站在学生角度给两个如此用心的孩子仔细分析，原因是周期的差异……分析完后，我也在思考教学中出现的这类问题，不难发现，这就是物理学中的一种特殊现象：同一个概念不同的物理意义,很明显,第一个例子中的密度是不瓦解的最小密度，是一种假设，不是真实情况，而第二个密度是真实的平均密度，是有科研价值的.那么，从学生的角度来看为什么会出现如此现象呢?结合这么多年的物理教学经验，我陷入了思考中.

1 对学生学习物理现状的思考

1.1 科学常识较少

物理学和生活结合比较紧密，问题本身源于教材，但必须有生活背景，有的直接是解决实际生活问题，有的涉及当代航天科技，有的体现体育盛事等等，需要学生有生活感知能力，具备必要的科学素养，如果连1 m具体多长，一个卧室面积大概多大都搞不清，怎么能学好物理知识.再比如很多学生对电源的输出功率和电源的工作效率是模糊不清的，对游标卡尺和螺旋测微器的测量精度和读数规则无法分辨，因此对上述两个密度混淆就很容易理解了.

1.2 课堂效率较低

一节课45 min，对于认真听课的学生觉得很快，甚至转瞬即逝，而对有些基础薄弱、接受能力差、自控能力不好的学生简直是如坐针毡，度日如年，可以想象他们的学习效率自然很低.当然这些学生一般成绩都不好，对他们来说确实听不懂，情有可原，然而并非只有这些学生效率低，也有一部分学生，他们的确在认真听课，但是只会听不会记笔记，俗话说：好记性不如烂笔头，如果不知道哪些是关键部分，只知道一个劲地听不做任何记录，结果课下大半忘记了，回忆不起来，只能说是事倍功半.还有一部分学生尤其是理科中的女生的确认真记了笔记，但是课下不巩固，不看笔记，把记笔记当成形式，做无用功.不少初学物理的学生有这种感觉，物理课一听就懂，一看也会，一做就错，感到束手无策，其实这正是说明物理课光靠认真听是不够的，必须眼脑手并用.对于物理概念不仅要记，更要理解，比如动能定理，就一句话：合外力做功等于动能的变化——然而它的内涵和外延远远不止这几个字这么简单.对于公式不仅会推导，关键要会用，就像运动学公式，有基本公式、推论、判别式、比例式，可以说是高中物理学公式最多的章节，如果学生不会分类，不知道运用条件和技巧，记住了也没用，不但没用，还容易混淆，越多越添乱.

1.3 运算能力较差

物理解题很大程度是考查学生的运算能力，数学运算能力一直制约学生学物理的深度和广度，要想把物理学到很深的层次上，必须强调学习数学的重要性，如同你要想把武功练到一定境界，你的内功心法必须达到一定层次.一道物理综合题实际就是一道数学综合题，纵观历年高考真题，没有很好的数学功底，要想解决好压轴题几乎是不可能的.高中阶段用的最多的数学知识内容主要有二次函数、三角函数、积分思想、微分思想、平面几何、解析几何……数学思维模式、运算习惯都在潜移默化地影响着物理.目前高中学生在学习物理时存在的数学问题主要有运算结果不彻底，不会化简，还有像公式错、结果错，公式对、结果错，公式错、结果对的几种现象.前两个还可以理解，后一个就觉得很蹊跷，我们不妨再看一个例子.

【例3】如图1所示的传送带沿着顺时针方向转动，A与B间距离足够长，速度v=4 m/s，一质量m=1 kg的物体轻放在传送带的A端，已知物体和传送带间的动摩擦因数μ=0.2，求物体从A运动到B过程中因摩擦而产生的热量.

图1 例3题图

错解：如图2所示，物体从A开始，受到向右的滑动摩擦力，由牛顿第二定律

Ff=μmg=ma

a=μg

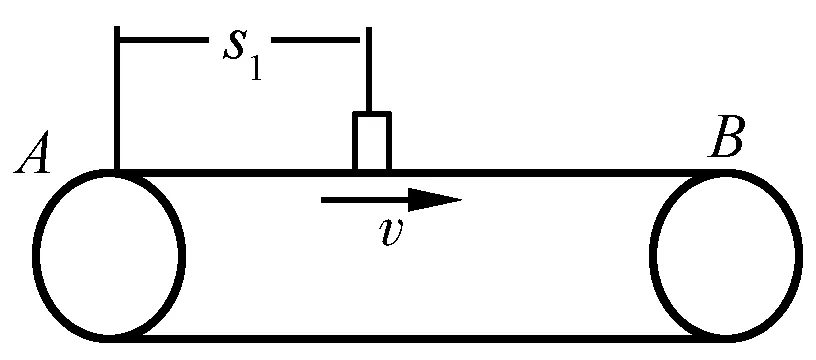
图2 分析物体位移

正解：如图3所示，传送带运动的位移

物体相对传送带的位移大小为

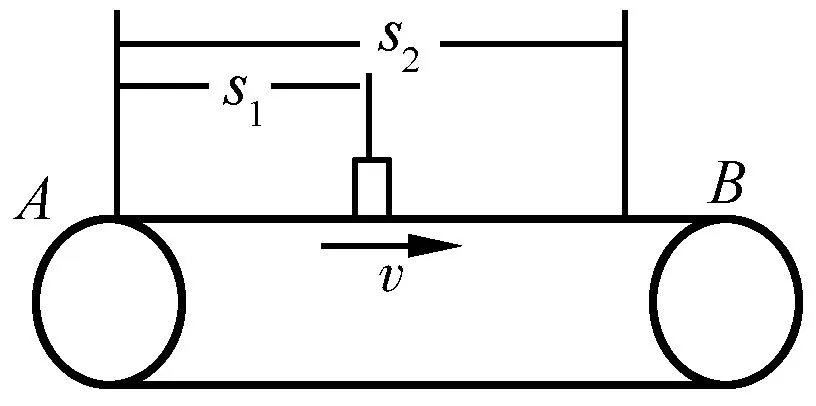
图3 分析传送带位移

正解和错解结果都一样，但是物理意义却完全不一样，这就是我们平常所说的用错误的方法得出正确的结果，然而常在河边走哪有不湿鞋，这种方法本身就是错误的，做选择题、填空题尚且可以蒙混过关，计算题是不得分的，或者改变条件，比如传送带加速，这种做法肯定是错误的.

1.4 参考答案较简

现行教辅资料很多答案不是很详细，描述简单，知识点分析不是很透彻，有的甚至只是简单地给一个结果，比如上面的例3，如果只看结果不看过程，做这道题不但没有提升能力，反而让自己养成一个错误的解题意识，遗留问题更大了.经常见到答案的经典描述性语言：“由上面式(1)、(2)得”，学生往往看了一眼答案，看到自己的结果和答案是一样的就认为自己是完全正确的，根本不会用心思考，如果让学生自己去推导，你会发现，他们往往“由式(1)、(2)”根本得不到预期结果，十分尴尬，原因是因为过程太简，过程跳跃幅度太大，对基础薄弱的学生不是答案，反而是负担.

2 对物理教学方法的思考

2.1 熟悉科学常识

从熟悉的生活入手，用科学常识解决实际问题，引导学生仔细观察，认真思考，了解其中的科学道理，并愿意参与科学活动，激发学生学科学、用科学的兴趣.同时让学生在活动中初步懂得生活中处处有科学，只要多留心、多动脑，就可以掌握更多的科学知识.在平时的教学中，有意识地以生活中的事例，介绍学生身边的科学常识，使学生了解生活中有很多科学知识.只有了解科学，运用科学知识，才会变得更聪明.另外课下引导学生关注媒体，关注新闻动向，关注体育赛事，关注航天科技……

2.2 提升课堂效率

课堂的45 min极其精贵，想提升课堂效率不能单靠哪一方面，不仅要求教师在备课、选题、选练上狠下功夫，还得需要教师在课堂教学方式上形式多样，体现教学魅力.同时要求学生在课堂上要学会眼耳手脑并用，学会听说读写练，笔记不仅要记更要会记，随堂练习不仅要快，更要准.只有师生配合才能完成高效课堂.

2.3 培养运算能力

现在的高考越来越重视运算能力，以2016年全国卷I为例，最后一道压轴题其实就是一个海量运算题，知识点难度不大，而运算难度大，所以综合难度指数大，导致得分不高.学生的运算能力差源于多方面的因素，一是教材的因素，高中物理课程在排列上和数学教材的排列上不能完全配套吻合，比如在高一一开始就讲矢量，而数学得到高一上学期快结束时才开始学习向量，两者之间在衔接和理解上出现间隙，导致学生理解上非常困难.二是教师因素，教师在课堂教学时，经常在演算中省略一些步骤，让学生课下演算，而有些关键步骤省略对学生是不利的，尤其是一些基础薄弱的学生，更是雪上添霜.三是学生的因素，学生在计算时借助于计算器，或者是看参考答案，教师要求课下演算也不去主动演算，导致演算能力越来越差.那么如何培养学生运算能力呢？首先得相信学生具备运算能力，让学生自己去真正地参与运算，有些时候可以把课堂上的一部分时间给学生，让他们当堂练习；其次精心设计作业，批改作业，出现计算失误的现象个别辅导，针对性纠正，让学生意识到，既要重视过程也要重视结果，不能因为计算而功亏一篑.

2.4 擅用参考答案

参考答案，顾名思义只能作为参考使用，有些过程简单直接，没有过程，甚至有些答案也有瑕疵，不能直接拿来使用，经常会出现参考答案中的诸如：由

2016-11-30)