旋转矢量法在夫琅禾费衍射中的应用*

汪连城

(南京工程学院数理部 江苏 南京 211167)

旋转矢量法在夫琅禾费衍射中的应用*

汪连城

(南京工程学院数理部 江苏 南京 211167)

应用简谐振动的旋转矢量表示法，将波动光学夫琅禾费衍射中复振幅叠加转换成旋转矢量的合成，并针对夫琅禾费单缝衍射和圆孔衍射的各级暗纹中心的衍射角和其在衍射屏上的位置进行了求解.相对于传统的基于惠更斯-菲涅耳公式的解析计算方法，基于旋转矢量合成的方法更为直观，对数学知识的需求相对较少，同时对大学生学习和理解夫琅禾费衍射以及其他波动光学问题具有一定的借鉴意义.

夫琅禾费衍射 暗纹中心 旋转矢量法 矢量合成

波动光学是大学物理的重要组成部分，而其中的夫琅禾费衍射，包括单缝衍射和圆孔衍射，是波动光学学习中的重点和难点.对于单缝衍射和圆孔衍射的衍射光强分布，在专业的光学教程中是利用惠更斯-菲涅耳公式，直接通过严格的推导得到[1]，但因其中包含较为复杂的积分以及贝塞尔函数的解析运算而对非物理专业学生来说显得较为困难.通过在直角坐标系下对波阵面进行条状分割，可以将求解积分过程中的二重积分化简为一元积分[2].也可以通过将求解叠加复振幅的积分函数展开成三角级数，利用三角函数的积分来替代需要利用贝塞尔函数的积分[3].此外，基于傅里叶变换的数值计算方法甚至可以得到任意形状的波阵面所对应的衍射光强分布[4].但无论哪种方法，都对非物理专业学生的数学知识或是数值计算知识提出了较高要求.更重要的，直接采用惠更斯-菲涅耳公式的解析或数值运算对于学生对波动光学物理机制的理解上效果有限.

在本文中，我们从简谐振动的旋转矢量表示法出发，采取和同方向、同频率的简谐振动合成的旋转矢量法[5]相类似的方法，对夫琅禾费单缝衍射和圆孔衍射的衍射机理和光强分布结果进行了深入的探讨.相对于传统的采用惠更斯-菲涅耳公式的严格方法，我们的思路更为简单和直观，所需的数学知识也相对较少，更为重要的是为理论知识有限的非物理专业学生学习波动光学提供了一种较为有效的理解

方式.

1 简谐振动的旋转矢量表示法及其合成

简谐振动的旋转矢量表示法[5]是指将简谐振动的位移、速度和加速度分别和一个长度为振动振幅、角速度为圆频率的矢量相对应.旋转矢量的端点在水平方向上的投影和简谐振动的位移相对应，矢量端点速度的水平分量和简谐振动的速度相对应，而矢量端点的向心加速度的水平分量和简谐振动的加速度相对应.在这样的设定下，两个同方向、同频率的简谐振动的合成就可以用两个旋转矢量的合成来简单地表达其结果.令A1和A2分别表示参与合成的两个子振动的旋转矢量，它们以共同的角速度ω绕坐标原点旋转，A是以A1和A2为边组成的平行四边形的对角线，同时A也是两个简谐振动的合振动的旋转矢量.这样，两个同方向、同频率的简谐振动的合振动也是简谐振动，其频率保持不变，而合振动的振幅就是A矢量的长度，合振动的初相就是零时刻A与x轴的夹角.特别的，如果两个子振动的旋转矢量A1和A2方向相同，则合振幅最大，为A1+A2；如果A1和A2方向相反，则合振幅最小，为|A1-A2|.

如果是多个振动方向和频率相同的简谐振动合成，则只需重复上述步骤即可求出合振动的旋转矢量.或者，更为直观地来看，多个同向同频简谐振动合成的合振动的旋转矢量就是各个子振动的旋转矢量的合矢量.由于旋转矢量是二维的，因此对于多个子矢量的合成问题，可以先将子矢量分别对水平、竖直两个方向求其投影，再分别将两个方向的投影分量进行加和，得到合矢量的两个分量，最后由这两个分量组合得到合矢量.

2 旋转矢量法在单缝衍射中的应用

在夫琅禾费单缝衍射中，根据惠更斯-菲涅耳原理，屏幕上某一点的光强将由单缝上所有子波波源的面积dS，子波到屏幕汇聚点的距离r和衍射角θ这3个因素共同决定.一般情况下，子波源到屏幕距离r和衍射角θ对子振动的振幅的影响可以忽略，这样每一个子波源在屏幕上的汇聚点所激发的子振动的振幅就正比于子波源的波面面积dS.而屏幕上某一点的最终光强，将正比于所有这些子波在该点所激发的振动的合振幅的平方.因此，对于求解屏幕上的光强分布问题，就等价于求解屏幕上某个点的合振幅问题.而合振幅的求解，就可以采取本文第一部分中所描述的方法，先将所有子振动所对应的旋转矢量放在一个矢量旋转平面上，再对这些旋转矢量进行合成求得合矢量，而合矢量长度的平方就正比于屏幕上该点的光强.如果是为了求解屏幕上光强分布的极值所在位置，那么就仅仅需要求解出合振幅何时取极值以及何时为零即可.

对于单缝波阵面上的子波的划分，可以将波阵面分割成一系列平行的长条，如图1所示.长条的水平长度和单缝的长度相同，令为a；而宽度取一个无穷小量dx，这样每一个子波长条的面积就是adx.根据薄凸透镜不引起附加的光程差原理，每一个长条上的各个子波到屏幕上汇聚点的光程是相等的，这样就可以把一个长条看成一个子波，每一个长条子波将在屏幕汇聚点上激发一个子振动.由于各个长条在竖直方向上排列，每个子波长条将在屏幕汇聚点激发出相位不同的子振动.这些子振动对应着一系列初相不同的子旋转矢量，只需要将这些子旋转矢量的合矢量求解出来即可.子矢量的长度和激发该子振动的子波面积成正比，而子矢量的相对位置将由它们分别对应的光线之间的光程差决定.这里描述的波阵面划分和合振动求解方法同样适用于其他类型的夫琅禾费衍射.

图1 夫琅禾费单缝衍射光路图

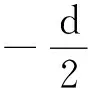
其中xsinθ是位置为x的子波和中心子波的光程差.接着对旋转矢量图上所有的旋转矢量进行分量的合成，其表达式分别为

和

这是一个初等函数积分，容易得到其表达式为

最后令

可得夫琅禾费单缝衍射振幅表达式为

其中C是常数，a是单缝长度，d是单缝宽度，而Ψ即为单缝发出所有子波所激发振动的最大相位差的一半.令A等于零，解得衍射角θ的取值,可得各级暗纹中心所在位置；令A的导数等于零，解得衍射角θ的取值，可得各级明纹中心所在位置.对于这个积分的极值和零值的求解，可以利用旋转矢量的分布结合对称性分析，得到合振幅的关键取值关于衍射角θ的分布，从而绕开复杂的解析运算.

图2 夫琅禾费单缝衍射旋转矢量图

3 旋转矢量法在圆孔衍射中的应用

在夫琅禾费圆孔衍射中，波阵面从狭缝变成了圆孔，在和单缝衍射相同的子波源分割方法下，即将圆孔型波阵面分割成一系列水平的长条子波源后，每一个子波源还是在屏幕上的同一汇聚点上激发一个子振动，这些子振动的合振动就决定了屏幕上该点最终的光强.但是由于圆孔衍射的波阵面是圆形的，因此分割出来的各个子波源的面积是不相等的，这和单缝衍射的情况不同，如图3所示.

图3 夫琅禾费圆孔衍射光路图

因此，圆孔衍射各个子波源在屏幕上汇聚点所激发的子振动的振幅是不等的，即子旋转矢量的长度是不相等的.根据惠更斯-菲涅耳原理，子旋转矢量的长度应该和子波源的面积成正比.由于子波长条的宽度取相同的无穷小量，因此子旋转矢量的长度就简单地和子波长条的长度成正比.这样，在同样满足在dsinθ=kλ,k≠0的衍射方向上，虽然各个子波所对应的旋转矢量的角位置还是中心对称地分布在原点周围，但是各子矢量的长度不一.如图4所示，位于圆孔圆心的子波带所对应的子旋转矢量A0的长度最长，而位于圆孔上沿、下沿的两个子波的子振幅最小，这样，在单缝衍射中应该是合成强度极小值的衍射方向上，到了圆孔衍射情形，其合振幅却不再是零.

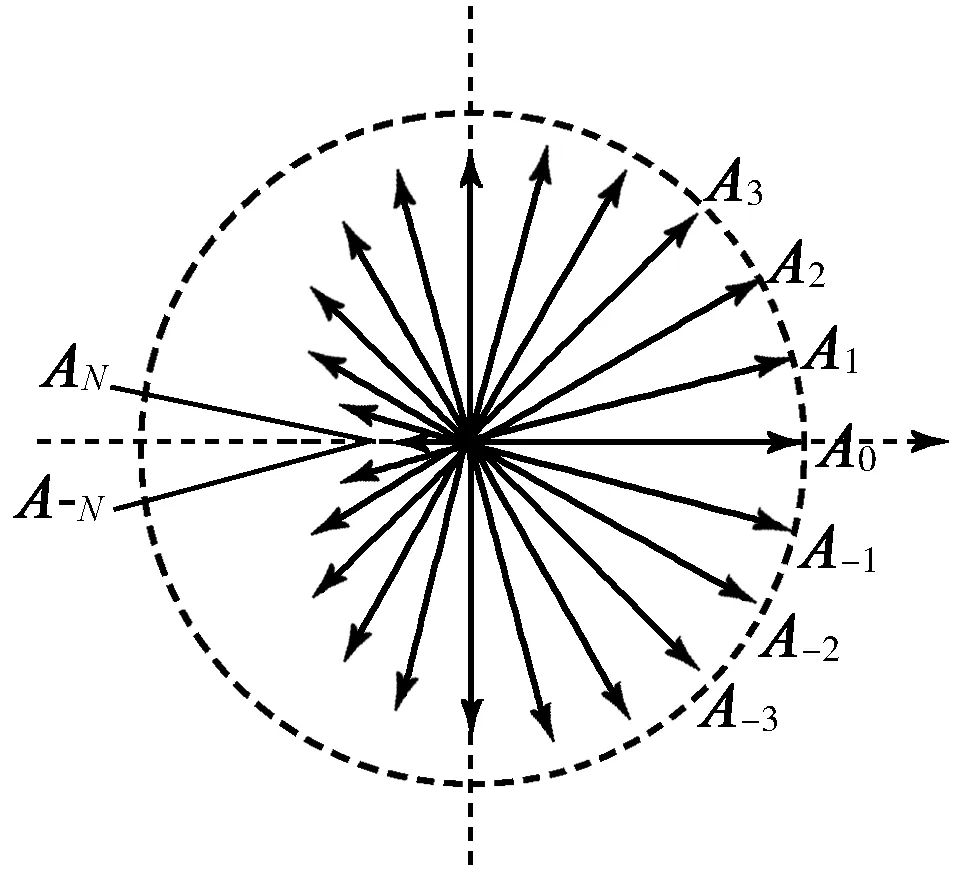
在最大光程差等于λ的衍射角下，各子旋转矢量的相位关于原点对称分布，但由于长度不等，因此合振幅并不为零.合振幅需要对各子旋转矢量进行积分计算

图4 夫琅禾费圆孔衍射旋转矢量图

初相为

根据对称性，圆孔上所有x>0的子波所对应的旋转矢量和所有x<0的子波所对应的旋转矢量应该对称地分布在A0的两侧，即关于x轴对称分布.这样在求解子旋转矢量的合矢量时，其y分量必然为零；而x分量的值取决于各子旋转矢量x分量的叠加.可以求得P点合振动旋转矢量x分量表达式为

Ax=2∫dAcosφ=

其中r为圆孔半径，C为常数.令

上式化简为

这个积分并不是简单的积分，无法直接从积分表上查询其积分函数.我们应用Mathematica的符号运算模块，并令

或

其中d为圆孔直径.可得

其中BesselJ[1,Ψ]为第一类一阶贝塞尔函数，而Ψ即为圆孔上发出所有子波所激发振动的最大相位差的一半.令合振幅为零即可计算出各暗纹中心所对应的各级衍射角.通过Mathematica的一元方程函数求解，并只取正实数解，可得Ψ≈3.83，7.02，10.17,13.32，…，转换成衍射角取值即

这个结果和利用惠更斯-菲涅耳公式计算结果一致(参考文献[1]表9-1).利用其中一级暗纹衍射角即

4 结束语

综上所述，利用简谐振动的旋转矢量表示法和同方向同频率简谐振动合成的旋转矢量法，对夫琅禾费单缝衍射及圆孔衍射的衍射光强分布进行了讨论，得到了两种衍射的各级暗纹中心位置分布.和传统的基于惠更斯-菲涅耳公式的方法相比，我们的方法更为直观，并且需要较少的数学知识，因此更利于非物理专业大学生对夫琅禾费衍射的学习和理解.本文提出的将旋转矢量的合成和惠更斯-菲涅耳原理相结合的思路对大学生深入学习和理解波动光学具有一定的借鉴意义.

1 母国光，战元龄.光学.北京：高等教育出版社，2009.194～222

2 戴又善，戴亮.推导圆孔夫琅禾费衍射光强分布分布的一种简便方法.大学物理，2009,28(4)：29～32

3 李春庭，李君.夫琅禾费圆孔衍射光强公式的一种推导方法.物理通报，2000(2)：14～15

4 谢佳宁，赵建林，陈伟成,等.夫琅禾费衍射的计算机仿真.大学物理，2004，23(3)：51～54

5 刘扬正，张伟强.物理学及其工程应用.北京：高等教育出版社，2015.126～128

ApplicationonRotationVectorMethodinFraunhoferDiffraction

WangLiancheng

(DepartmentofMathematicsandPhysics,NanjingInstituteofTechnology,Nanjing,Jiangsu211167)

Applying rotational vector notation for the harmonic vibration, the superposition of optical waves in Fraunhofer diffraction is converted to composition of rotational vectors. The positions of the centers of dark patterns in the Fraunhofer diffraction on single slit and circular aperture are calculated. Compared with the calculations based on the Huygens-Fresnel formulas, our method is more intuitive and requires relatively less mathematical knowledge. Our approach can also help understanding in the study of Fraunhofer diffraction and other issues in wave optics for college students.

Fraunhofer diffraction; centers of dark pattern; rotation vector method; composition of vectors

*南京工程学院创新项目，项目编号：CKJB201509

2016-09-28)