基于正交试验法的B柱抗弯性能研究与优化*

莫易敏 谢业军 徐 芳 梁永彬 林智桂

(武汉理工大学机电工程学院摩擦学研究所1) 武汉 430070) (上汽通用五菱汽车股份有限公司2) 柳州 545007)

基于正交试验法的B柱抗弯性能研究与优化*

莫易敏1)谢业军1)徐 芳1)梁永彬1)林智桂2)

(武汉理工大学机电工程学院摩擦学研究所1)武汉 430070) (上汽通用五菱汽车股份有限公司2)柳州 545007)

B柱作为侧围结构的主要构件，其抗弯性能将影响整车侧面碰撞结果.基于三点弯曲试验设计，结合有限元仿真技术对B柱结构进行了等效简化.采用正交试验法，对外板的厚度和材料、内板的厚度和材料、截面长宽比这5个变量组成的样本空间进行样本点的抽取.通过有限元仿真分析，得到该5个要素对抗弯性能的影响规律，即外板材料对比吸能的影响最为显著；而外板厚度对加载力峰值的影响最为显著，外板材料次之.利用极差方差分析法，获取各因素的最佳水平，获得兼顾了加载力峰值和比吸能最优的参数组合，并通过三点弯曲试验仿真验证了优化结果的有效性.

侧面碰撞；B柱；有限元分析；正交试验法；抗弯性能

0 引 言

侧面碰撞占车辆碰撞事故的比例较高，造成乘员伤亡率重伤和死亡率高达25%[1].近些年来，国内外的诸多学者对侧面碰撞安全做了相关的研究.Chen等[2]通过一种简化的弯曲试验对B柱、门槛梁的截面形状做了优化.优化的准则是使零部件的单位质量的吸能最大.张文[3]根据对汽车B柱的特点将其简化成薄壁梁构件；之后对采用不同的高强度钢薄壁梁构件进行三点弯曲试验，主要研究不同材料、厚度下单个因素对其抗弯曲变形的特性.曲晓庆等[4]主要对B柱部位的材料进行更改：将B柱内板材料由B340/590DP改为B410LA；B柱內加强件的材料由B340/590DP改为B410LA.其改进后优化效果明显，提高了整车耐撞性能.可以看出，这方面的研究主要是通过改变B柱的一个或两个因素进行的，而对多因素影响规律的研究较少.

侧面碰撞时，主要变形区是汽车的侧围部分.而影响汽车侧面碰撞性能的零部件主要是车门、车门防撞梁、B柱及门槛梁等薄壁构件[5].

B柱是侧围零部件中最为关键的部件之一，其耐撞性往往决定了整车的侧面碰撞安全性能.但如果在整车中对B柱进行CAE仿真研究，计算量庞大，计算时间长久.加上B柱本身具有变截面的结构特点，不易得出一般性规律.因而文中应用了三点弯曲试验，对薄壁件B柱的抗弯性能进行研究[6].基于三点弯曲试验设计，结合有限元仿真技术对B柱结构进行了等效简化，再利用简化模型作为母体，将内板厚度和材料、外板厚度和材料以及截面长宽比这五个因素作为研究内容，采用正交试验法选取仿真实验样本点，分别建立各样本点仿真模型，经过LS-DYNA计算后，对结果进行分析处理，进而研究薄壁梁的抗弯性能，并验证采用正交试验法的优化效果.

1 研究对象与评价指标

1.1 研究对象

薄壁结构是一种常见的吸能部件，广泛应用于汽车、船舶等领域.金属薄壁构件作为最传统、最有效的缓冲吸能装置，在车身吸能设计的体系中已得到广泛应用[7].本文主要的研究对象是汽车侧围中具有金属薄壁结构的B柱.B柱总成见图1.

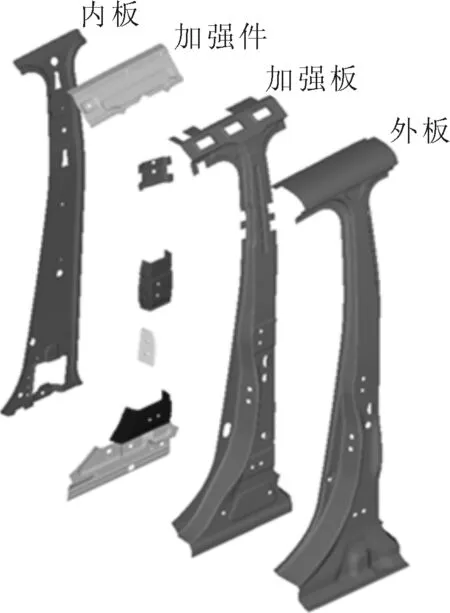
图1 B柱总成结构示意图

汽车B柱是侧围结构中最重要的承载件，除了满足外观造型的设计要求外，还需要满足一定的强度和刚度，在侧面碰撞过程中保证较好的力传递性能.然而由于整车模型数据量庞大，对单个零部件进行结构优化时，若采用整车进行仿真，优化过程会耗费大量的计算时间和人力资源.此外，由于在碰撞过程中可移动变形壁障(MDB)和B柱为面接触，车身B柱结构的吸能主要是以金属薄壁结构的横向弯曲为主要破坏模式的能量耗散过程；而在三点弯曲试验中，压头为线接触，为了获取较为经济且直观的解析过程，同时不发生局部效应，以更好地看出零部件全局变形，所以采用准静态试验，因此，在对B柱进行单独的零部件研究时，采用模拟实际工况的准静态三点弯曲试验[7].

导入UG中画好的内外板几何模型图到HyperMesh中；以Shell单元建立薄壁梁模型；内板下部添加两根刚性圆柱作为简支支撑，这种情况下的B柱变形形式更为接近于整车侧碰中的B柱变形；以MAT100材料建立焊点单元连接内外板；设置圆柱刚性墙压头，作用总时长为180 ms，以1 mm/ms速度下压，模拟准静态力学实验过程；最后设置好各接触类型与输出控制卡片.最终建立好的三点弯曲试验有限元模型见图2.

图2 三点弯曲试验有限元模型图

1.2 评价指标

为了评价B柱在弯曲载荷作用下的力学性能，采用以下指标：

1) 加载力峰值Fpeak 加载力峰值是在整个碰撞过程中出现的最大加载力，反映了薄壁件最大的过载情况.它对于结构的耐撞性有着重要意义，在碰撞过程中，加载力峰值要求小于某一个阀值，以避免对系统中的部件造成不可修复的伤害.

2) 能量吸收(energy absorption,EA) 在模拟实际工况的三点弯曲试验中，万能试验机的输出为力-位移曲线.要用能量吸收来反映试验样件抵抗变形的能力，故对曲线进行数学方法处理得到加载过程中所吸收的能量大小.能量吸收EA的计算式为

(1)

式中:s为位移变量；F(s)为加载力.

3) 比吸能(specific energy absorption,SEA) 比吸能是一个有量纲评估指标，表现了结构单位质量的能量吸收能力，是耐撞性与轻量化设计中的最重要的指标之一.比吸能由结构在加载过程中所吸收的总的能量EA除以结构总的质量m得到，比吸能SEA的计算式为

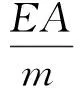
(2)

式中：m为梁质量.

文中采用上述的加载力峰值和比吸能这两个指标来评价B柱在弯曲载荷作用下的力学性能.

2 建立B柱简化模型

为了在后期研究中突出单一研究要素对抗弯性能的影响，同时减少B柱试验样件的制造难度和成本，因此需要简化B柱结构.通过有限元仿真，讨论由于结构避让或者功能件安装等原因而在B柱上布置的B柱孔洞结构、倒角及加强肋、曲面弧度以及结构梯度等对三点弯曲结果的影响，从而对B柱结构进行适当的简化设计.进过仿真实验对比结果发现，B柱孔洞结构、倒角及加强肋、曲面弧度等对其抗弯性能的影响都较小，最大误差均在5%以内.根据Kecman弯曲理论模型，矩形薄壁梁发生弯曲时是在褶皱区域产生塑性铰转动吸能，而薄壁梁其他区域仅发生刚性转动，所以在做研究时可以忽略B柱非褶皱区域内的特征结构以方便后期建模和实物加工.又由于汽车发生侧面碰撞时，B柱主要受力部位在MDB上端水平面内的B柱截面位置处，此处受到的转矩最大，结构最为薄弱，故B柱简化模型的截面原型选用此中间位置附近的截面.

对于B柱结构，拟采用等截面的平直梁进行等效简化，MDB上端水平面内的B柱截面a见图3a).该截面的倒角及不对称结构等不利于后期零部件的加工制造，需要对该截面进行调整.在截面周长不改变的前提下，删除结构的倒角，并将形状调整为对称形式，调整后的截面b见图3b).为了方便后续三点弯曲试验仿真的样本点设计，进一步把截面焊接边调整到中间位置，使其成为上下、左右均对称的截面结构，调整得到的最终简化截面c见图3c).

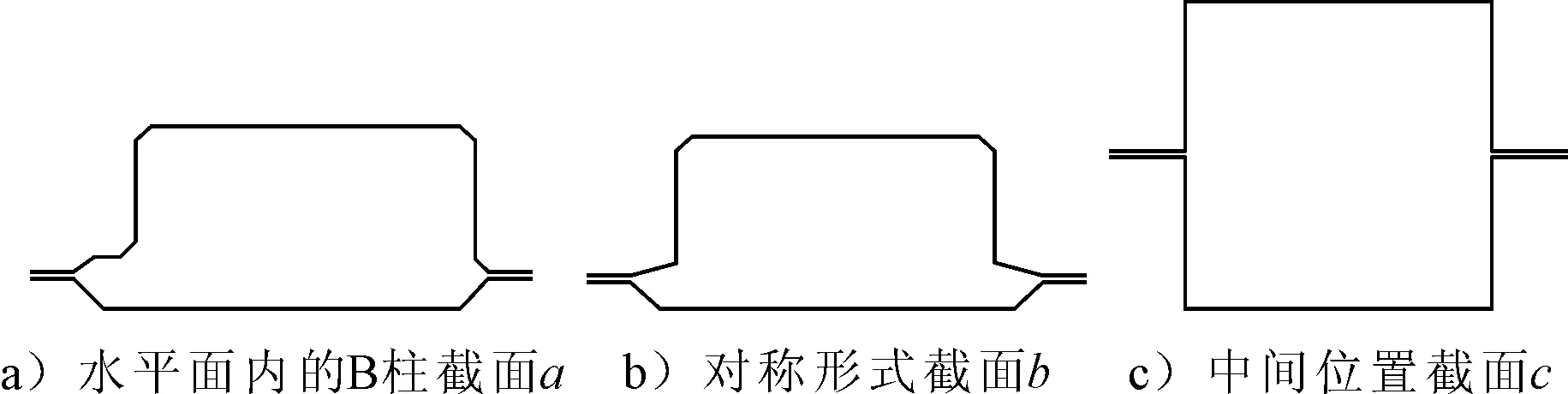
图3 B柱各简化结构截面示意图

以上截面简化过程的三点弯曲试验仿真结果见图4.简化截面结构b，c均能较好的复现原结构的仿真曲线，三条曲线的加载力峰值相差无几，曲线走势基本一致.

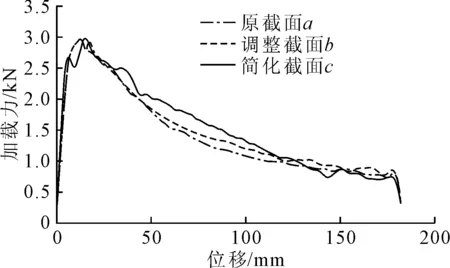
图4 简化结构梁的加载力位移曲线图

为了在后期研究中突出单一研究要素对抗弯性能的影响，同时减少B柱试验样件的制造难度和成本，确定采用以正对称的简化结构截面c的平直简单双帽形梁作为B柱的简化结构进行后期研究.

3 正交试验设计

3.1 试验目标的确定

研究基于某公司的某车型，对其统计可得，B柱内外板厚度均为0.8 mm，外板材料为DC06，内板材料为SPCC.试验的目标设定为比吸能Y1(单位：J·kg-1)和加载力峰值Y2(单位：kN).

3.2 试验因素和水平的确定

选用外板的厚度(A)和材料(C)、内板的厚度(B)和材料(D)，以及截面长宽比(E)作为试验的5个因素，各个因素取7个水平，其值的大小和选取是根据对某公司现有几款车型的B柱板厚及用材等情况进行数据统计后得出的.正交试验因素与水平见表1.

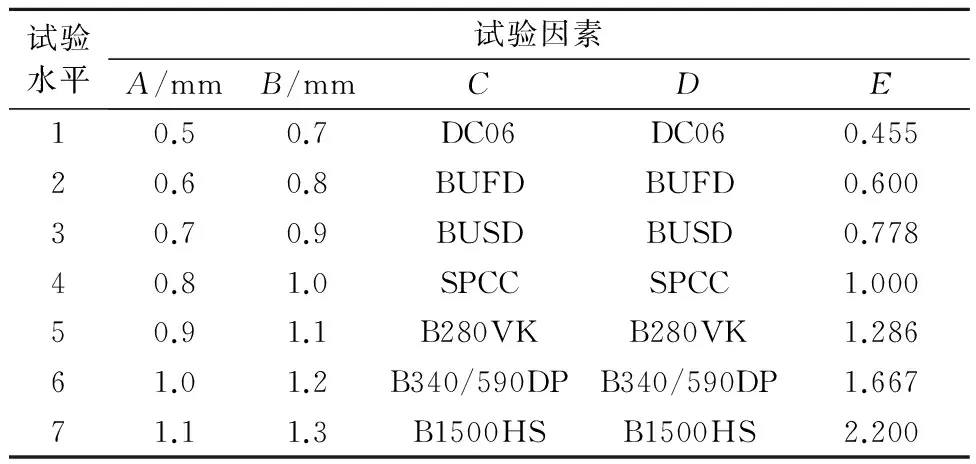
表1 正交试验因素与水平

3.3 正交表的选用以及数值模拟

根据表的因素和水平，采用5因素7水平的正交试验来进行设计.按照表1所设置的参数方案进行仿真模拟实验，并得到相应的模拟结果见表2.其中，0号试验是基于某车型各因素原始参数组合.

4 结果分析与验证

4.1 极差方差分析

为了更加直观地得出不同试验因素取不同水平时对比吸能和加载力峰值的影响程度，对表2的数据进行极差分析和方差分析.其中，均值的计算方法是将各个因素各个水平的仿真结果相加再分别除以各因素的水平数；极差的计算方法是将各个因素不同水平的均值的最大值减去最小值；最后通过极差的大小来分配各个因素的权重，极差越大，权重越大，反之越小.方差分析是将试验指标的总体变化分解为来源不同因素的相应的变化，从而得出各个因素在总体变化中所占的重要程度，方差表中的各个数值由SPSS软件计算得出[8].极差分析结果见表3.

从表3的结果可知：

1) 因素C(外板材料)对薄壁件B柱的比吸能影响最大，在研究的参数范围内，外板材料屈服强度越大，比吸能一般也越大；因素E(截面长宽比)次之，在所研究的范围内，截面长宽比越小，比吸能越大；因素A(外板厚度)对比吸能也有一定的影响，而因素D(内板材料)与因素B(内板厚度)对比吸能的影响不是很明显.故影响比吸能的主次因素依次为：C>E>A>D>B.对于B柱来说，比吸能越大说明其吸能特性越好，即每个因素在不同水平下的比吸能应该越大越好，可以得出在所研究的范围内，使比吸能最大的最佳工艺参数组合是：A7B3C7D7E1.

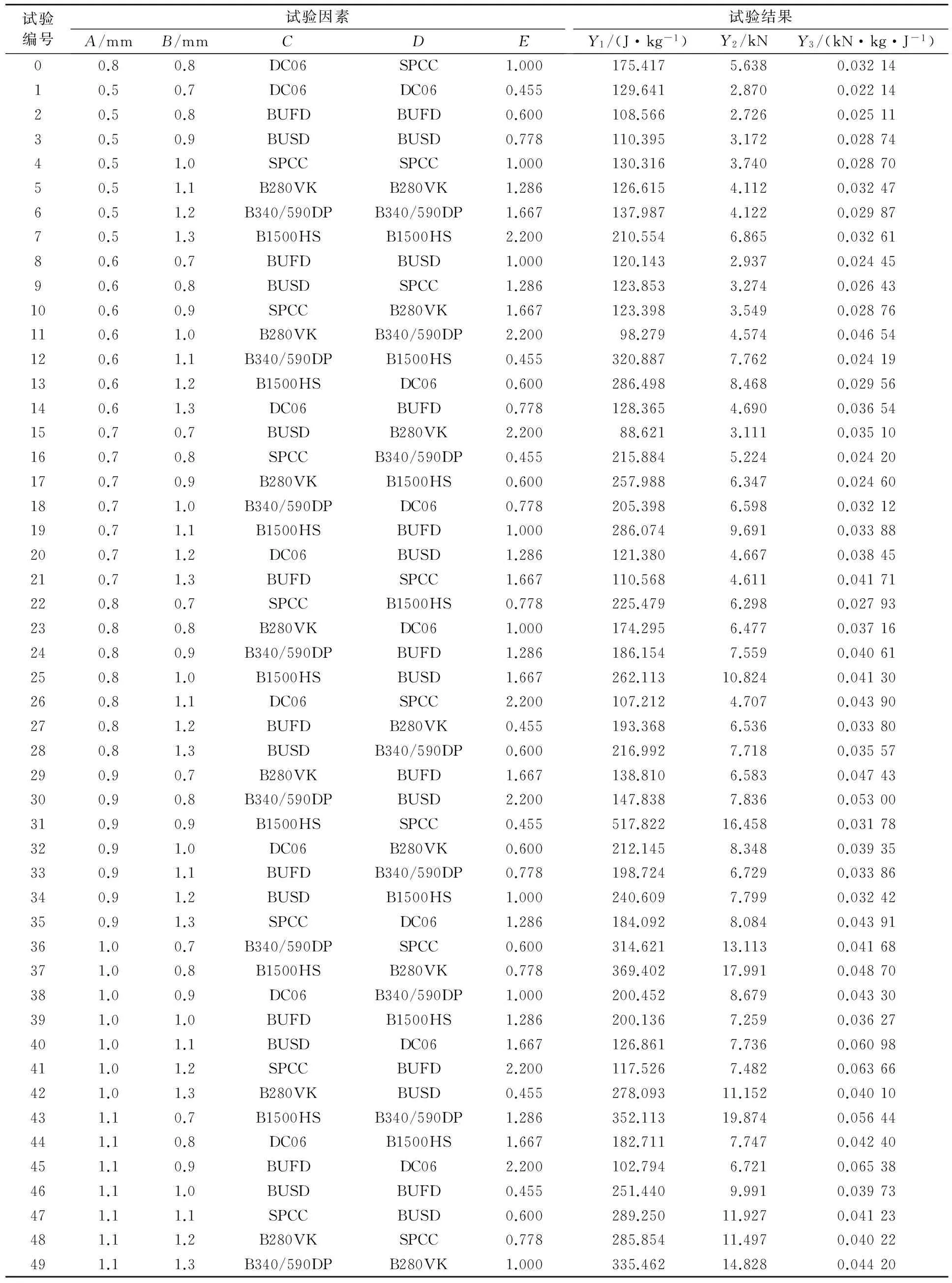
表2 正交试验方案与结果

2) 因素A(外板厚度)对B柱的加载力峰值影响最大，在所研究的范围内，外板厚度越小，加载力峰值也越小；因素C(外板材料)次之，外板材料屈服强度越小，加载力峰值一般也越小；因素E(截面长宽比)、因素D(内板材料)与因素B(内板厚度)对加载力峰值的影响不是很明显.故影响加载力峰值的主次因素依次为：A>C>E>D>B.

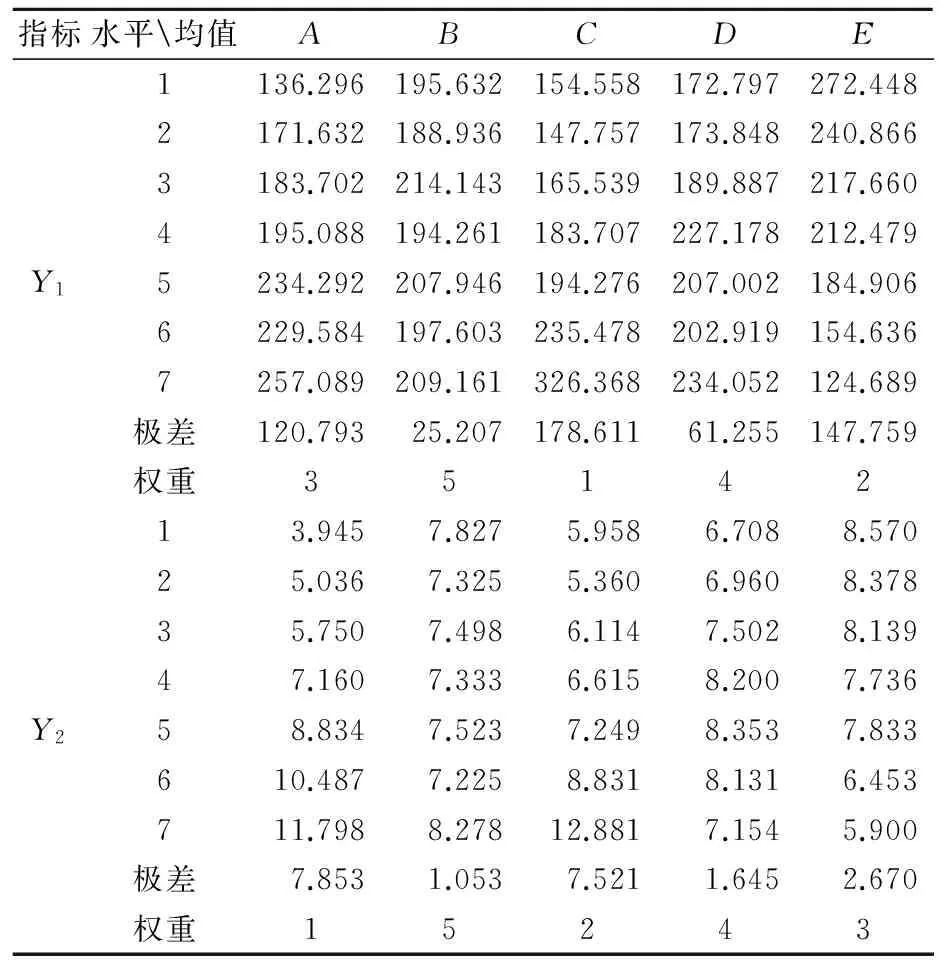
表3 比吸能与加载力峰值极差分析表

加载力峰值越小说明其抵抗最大冲击的能力越好，即每个因素在不同水平下的加载力峰值应该越销越好，可以得出在所研究的范围内，使加载力峰值最小的最佳工艺参数组合是：A1B6C2D1E7.

通过分析Y1和Y2这两个指标的最优因素水平发现，若要达到高比吸能要求，则其加载力峰值较大；若要加载力峰值小，则比吸能条件不能兼顾.也就是说，上述对单个指标分析无法确定参数的最优值.因此，考虑到加载力峰值与比吸能的要求，重新构造综合指标Y3(单位：kN·kg·J-1)，将多指标优化转化为单指标优化.Y3计算方法见式(3)的Y3结果见表4.

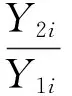
(3)

式中：i为试验号.

通过对表2的Y3进行同样的极差分析和方差分析，得到结果见表4～表5.对Y3的极差分析方法同上.由表4可知：综合指标Y3而言，影响Y3的主次因素依次为：A>E>D>B>C；在所研究的范围内，使Y3最小的最佳工艺参数组合是：A1B1C4D7E1.

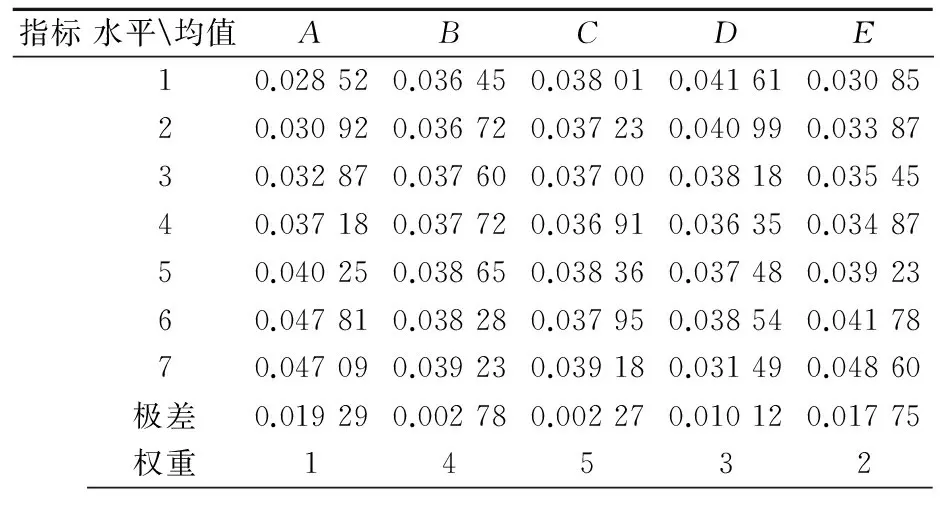
表4 Y3极差分析表

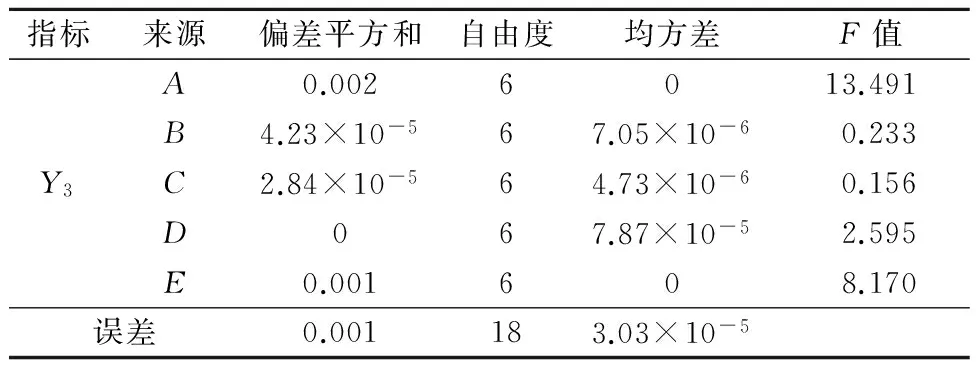
表5 Y3方差分析表

方差表中的F值代表了各个因素对于指标的影响程度.由表5可知,影响Y3的主次因素依次为：A>E>D>B>C.其中，因素A与因素E对Y3的影响较大，即外板厚度与截面长宽比对梁的弯曲性能影响最大，方差分析与前面的极差分析结果具有很好的一致性.

4.2 结果模拟验证

通过上述正交试验设计及优化分析可知，对于本次优化，综合考虑薄壁件B柱的比吸能及加载力峰值，在所研究的范围内，得出的最优因素水平组合为：A1B1C4D7E1，即外板厚度取0.5 mm、内板厚度取0.7 mm、外板材料取SPCC、内板材料取B1500HS、截面长宽比取0.455(长50 mm/宽110 mm).优化前后各个因素的水平组合见表6.在三点弯曲试验模型中按照优化后的参数设置进行模拟验证，得到的比吸能Y1为320.611 J·kg-1(优化前Y1值为175.417 J·kg-1)，比吸能优化效果为82.77%；优化后得到的加载力峰值Y2为3.618 kN(优化前Y2值为5.638 kN)，加载力峰值优化效果为35.82%；优化后得到的综合指标Y3为0.011 29 kN·kg/J(优化前Y3值为0.032 14 kN·kg/J)，Y3的优化效果为64.87%；各个评价指标的优化效果都相当明显.优化前后的加载力位移曲线对比图见图5.

表6 优化前后各个因素的水平组合对比

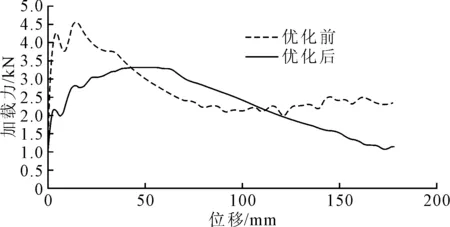
图5 优化前后加载力位移曲线图

由图5可知，加载力峰值明显降低，曲线总体趋势也更平缓.再通过将优化后得到的Y3值与表3的Y3值进行比较，可见优化后的Y3值均小于优化前的Y3值，表明了利用正交试验法进行比吸能优化及加载力峰值优化，即抗弯性能优化的准确性.

5 结 论

1) 在所研究的5个因素中，外板材料对比吸能的影响最为显著，而内板厚度和材料对比吸能的影响不是很明显；外板厚度对加载力峰值的影响最为显著，外板材料次之，而剩下的三个因素对加载力峰值的影响几乎可以忽略不计.换言之，对B柱的抗弯性能进行研究时，主要的研究对象应为外板.

2) 在研究的参数范围内，外板材料屈服强度越大，截面长宽比越小，比吸能一般越大；外板厚度和材料屈服强度越小，加载力峰值也越小.

3) 在最优的参数组合下，实验仿真模拟得的综合指标Y3值均比正交表中的试验结果要小，从而验证了利用正交试验法来优化B柱抗弯性能的有效性.

[1]WANG D Z, DONG G, ZHANG J H, et al.Car side structure crashworthiness in pole and moving deformable barrier side impacts[J]. Tsinghua Science and Technology,2006,11(6):725-730.

[2]CHEN G, SHI M F, TYAN T. Optimized AHSS structures for vehicle side impact[J]. Sae International Journal of Materials & Manufacturing,2012,5(2):304-313.

[3]张文.基于侧面碰撞的高强度钢耐撞特性以及相关选材技术研究[D].长沙：湖南大学,2012.

[4]曲晓庆,胡丽娟,乔鑫.基于C-NCAP某车侧面碰撞分析优化[C]∥中国汽车工程学会,2015中国汽车工程学会年会论文集，2015.

[5]刘卫民,刘卫国,管立君.某微型汽车侧面碰撞安全性能优化[J].汽车技术,2011(10):24-27.

[6]胡海涛.帽型薄壁梁抗弯性能研究及多目标优化[D].大连：大连理工大学,2015.

[7]YIM H J, LEE S B, PYUN S D. A study on optimum design for thin-walled beam structure of vehicles[J]. SAE Technical Paper,2002(1):55-58.

[8]刘瑞江,张业旺,闻崇炜,等.正交试验设计和分析方法研究[J].实验技术与管理,2010(9):52-55.

A Study on the B-pillar’s Bending Performance and Optimization Based on the Orthogonal Experiment

MO Yimin1)XIE Yejun1)XU Fang1)LIANG Yongbin1)LIN Zhigui2)

(School of Mechanical and Electronic Engineering, Wuhan University of Technology, Wuhan 430070, China)1)(AIC-GM-Wuling Automobile Co. Ltd., Liuzhou 545007, China)2)

As the main element of the side parts, B-pillar’s bending performance will affect the vehicle side impact results. By combining the three-point bending test with finite element analysis, the B-pillar is equivalently simplified. The orthogonal experiment is used to extract sample points in the sample space composed of 5 factors including the external plate’s thickness and material, inner plate’s thickness and material, cross-sectional aspect ratio. After finite element analysis simulation, the influence of 5 factors on the bending performance is showed. The external plate’s material has the greatest impact on specific energy absorption, and external plate’s thickness and material are the two most important factors influencing the peak loading force. Range analysis and variance analysis are used to acquire the optimum level of individual factor. The optimized parameters combination is also obtained, by taking the peak loading force and specific energy absorption into account. The results of the simulation have validated the effectiveness of the optimization.

side impact; B-pillar; finite element analysis; orthogonal experiment; bending performance

2017-30-20

*校企合作基金项目资助(S-C08-01W10-904-010-OR88)

U467.1

10.3963/j.issn.2095-3844.2017.03.005

莫易敏(1960—)：男，博士，教授，主要研究领域为摩擦学、机电一体化、汽车安全等