哥德巴赫猜想双无解定理的表证法

叶雉鸠

(陕西财经职业技术学院，陕西 咸阳 712000)

哥德巴赫猜想双无解定理的表证法

叶雉鸠

(陕西财经职业技术学院，陕西 咸阳 712000)

提出了哥德巴赫猜想的一个不缺项的双无解定理。若这个不缺项双无解定理成立则哥德巴赫猜想成立，若这个不缺项双无解定理不成立则哥德巴赫猜想不成立。这个不缺项的双无解定理可以用同余数表进行表示。用同余数表进行递推证明的方法比较直观，而且没有悬念。本文运用数学归纳法证明了哥德巴赫猜想成立。

哥德巴赫猜想；不缺项双无解定理；同余数表；数学归纳法

首先定义几个集合：

{奇素数}={3，5，7，11，……}=P

{不大于2a的奇素数}={3，5，…，pk}=Pk⊆P

a≥5且a∈N。

1 一个引理及其证明

1.1 引理1的提出

引理1 对于每个大于10的偶数2a+2(a≥5，a∈N)下的方程组(1)①，如果y取某个定值y0时方程组(1)无正整数解，那么y为任意自然数时方程组(1)恒无正整数解；如果y取某个定值y0时方程组(1)有正整数解，那么y为任意自然数时(1)恒有正整数解。

(1)

1.2 引理1的证明

如果y取y0时方程组(1)有正整数解，则方程组(2)②有正整数解。

(2)

因为方程组(2)有正整数解，这时，在方程组(2)两边同时加上任意的2y(自然数)，同余式方程组仍然成立，即方程组(1)有正整数解。

反之，如果y取y0时方程组(1)无正整数解，则方程组(2)无正整数解。这时在无解的方程组(2)两边同时加上任意的2y(自然数)，同余式方程组仍然无解，即方程组(1)恒无正整数解。

证毕。

2 不缺项的双无解定理

2.1 定理1的提出

定理1 对于每个大于10的偶数2a+2(a≥5，a∈N)，下列方程组(3)①和方程组(1)同时无正整数解。该定理简称为“不缺项双无解定理”。

(3)

这个方程组的意义可参阅《采用缺项双无解定理证明哥德巴赫猜想》一文[3]。

“不缺项的双无解定理”的同步性证明可参阅《采用双无解定理证明哥德巴赫猜想》一文[4]。

2.2 定理1方程组(3)的同余数表

将定理1中方程组(3)用同余数表来表示，可以得出定理2。

定理2 对于每个大于10的偶数2a+2(a≥5，a∈N)都可以构造一个如表1所示的同余数表，该同余数表中至少存在一行无零，即整行余数不能出现一个零。

表1 定理2对应于2a+2的同余数表

表1中y≥a，表1显示的同余数是否“至少存在一行无零”？与方程组(3)所示的同余关系 “是否有解”具有对应关系。如果表1中“至少存在一行无零”，即方程组(3)无解。反之，如果表1中“各行都至少有一个零”，则方程组(3)有解。

3 不缺项双无解定理的证明

3.1 代入初始值检验

见于“不缺项双无解定理”的方程组(3)和方程组(1)在有解或者无解这个问题上具有同步性，所以初始值检验只用验证方程组(3)无解即可。

当2a=10时，Pk中有三个元素3、5、7，Pb中仅有一个元素3，其所对应的同余数表如表2所示③。

表2 10+2对应定理2的同余数表

表2中最下行显示相对于模3，余数非零的行数。表2中有均两行无零，故定理2成立。定理2成立即方程组(3)无解。

当2a=12时，没有引起Pb变化，但是Pk当中多了一个元素11(第Ⅱ种情况)，其所对应的同余数表如表3所示④。

表3 12+2对应定理2的同余数表

表3中至少有两行无零，故定理2成立。定理2成立即方程组(3)无解。

当2a=14、18、20、24时，没有引起Pb变化，但是Pk当中多了一个元素，这都属于第Ⅱ种情况。

2a=24以前相对于模3的同余数表如表4所示⑤。

当2a=16、22时，没有引起Pk和Pb变化(第Ⅰ种情况)。根据引理1，其所对应的同余数表至少有一行无零(表4中真值显示，y=8、11时，非零行分别为4行和6行)，故定理2成立。

当2a=26时，没有引起Pk变化，但是Pb当中多了一个元素5(第Ⅲ种情况)，其所对应的同余数表与2a=24所对应的同余数表的行数相同，但是模却多了一个元素5。此时，2a=26所对应的同余数表如表5所示⑥(表5的完整表见附表“哥德巴赫猜想的同余数表”)。

表5中最下行显示相对于模3和模5，余数同时非零的组数。表5中y=13，pki=3的两个单元格很关键，它是模5出现后，余数方有零的单元格。表5中，Pk中含有八个元素3、5、7、11、13、17、19、23，Pb中仅有两个元素3、5。表5中相对于Pk至少有两行无零，故定理2成立。定理2成立即方程组(3)无解。

观察表5中y=12、13两列，y从12到13能保持定理2成立的两条证明思路是：

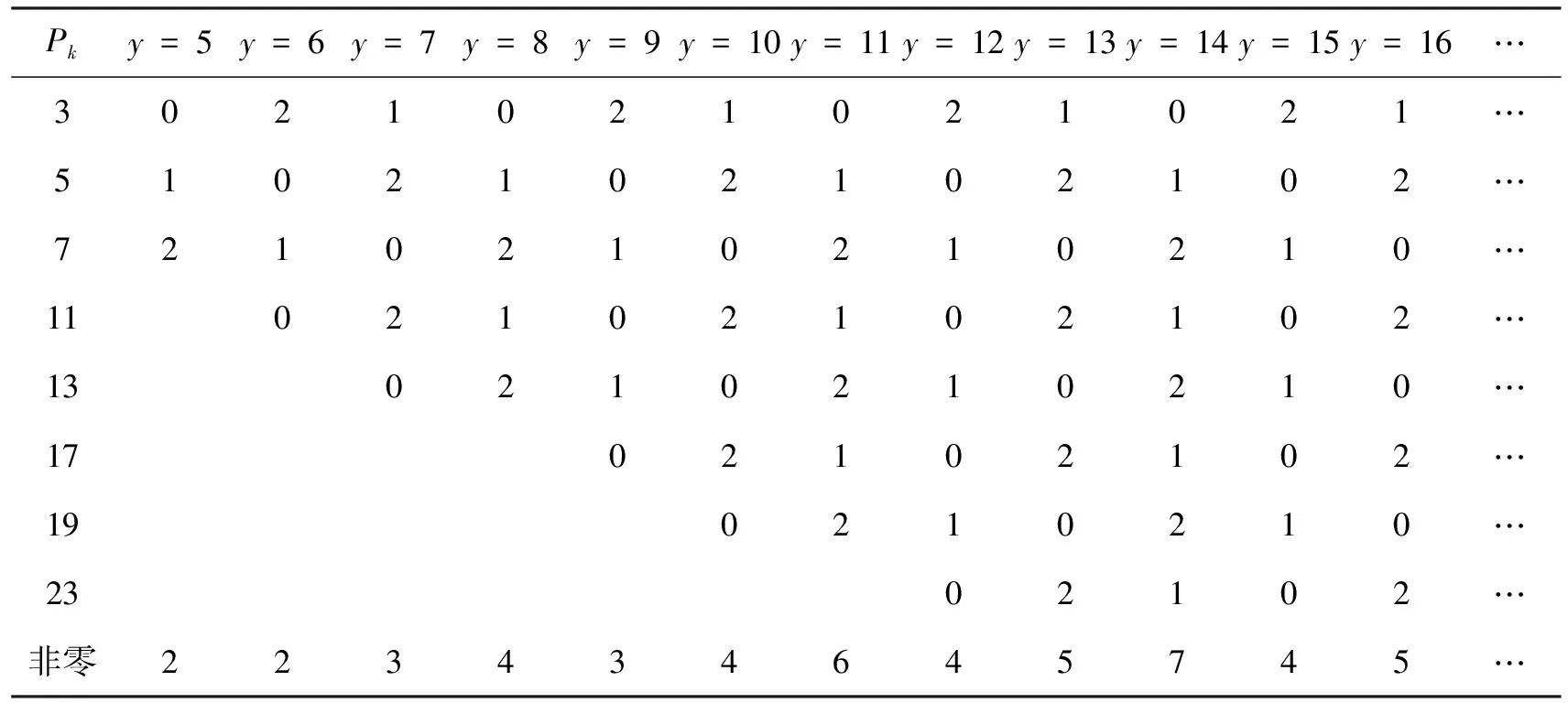
表4 24+2以前对应定理2的同余数表

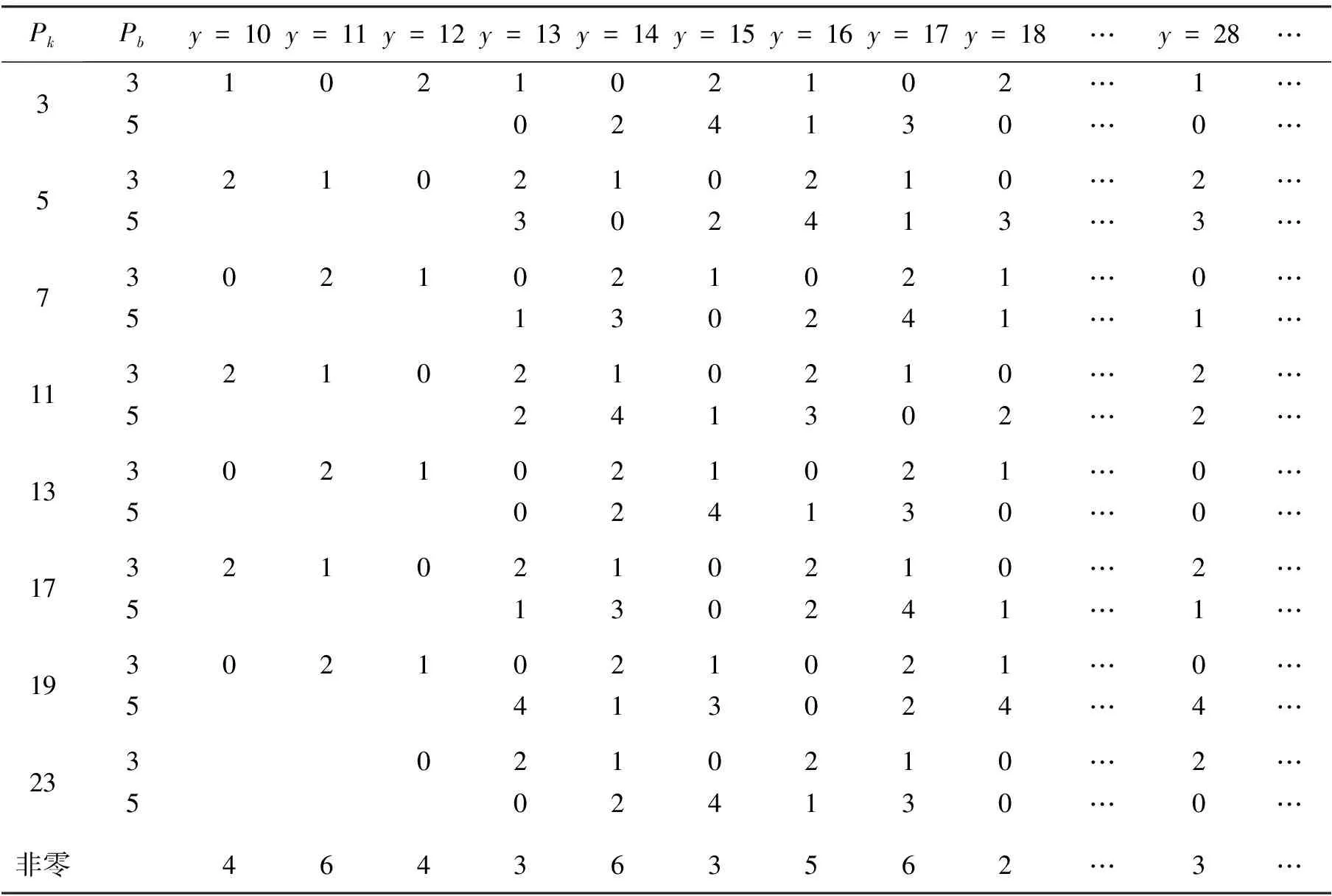
表5 26+2对应定理2的同余数表

(1)反证法

反证法的假设：当y=12时定理2成立，y从12变动到13，因为模5的出现使得定理2不成立。该假设是说：当y=12时，表5中Pk的所有元素相对于模3的单元格内至少有一个余数非零；当y=13时，表5中Pk的所有元素分别相对于模3和模5的那两个单元格内均至少有一个零。

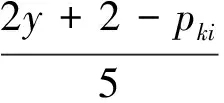
反证法的推导：当y=13时，pki=3，即表5中相对于模3和模5的两个单元格显示模5的出现使得该单元格的余数为零。表5中y=13这一列向下的其他单元格，其整除性不受模5出现的影响。

根据“当y=13时，定理2不成立”的假设，由定理1的方程组(3)得出方程组(4)有解

(4)

因为模5的出现仅对pki=3起作用，所以由方程组(4)得出方程组(5)有解

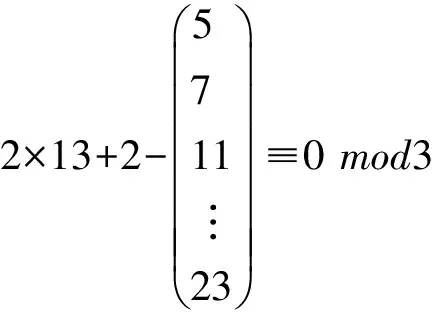
(5)

方程组(5)很显然是无解的——出现矛盾。故对于2a=26，定理2成立。

(2)存在无效列法

由表5可以看出，当y=16、24、27及其以15为间隔的自然数，如31、39、42等等时，模5的出现并不能使得模3的非零余数为零。即y=16、24、27、31、39、42等各列，相对于模5的余数为零时，模3的余数原本就是零；相对于模5的余数不为零时，模3的余数无所谓是零或者不是零。以y=16为例：

由定理1的方程组(3)得出方程组(6)有解

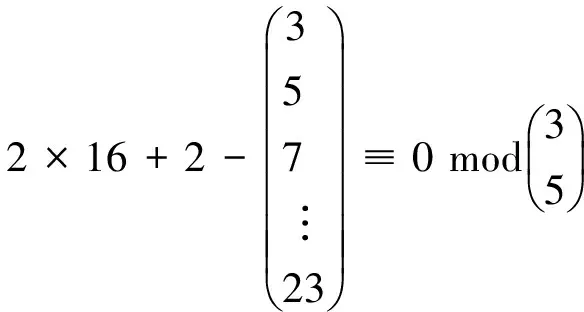
(6)

因为模5仅在pki=19时余数为零，但是模3在pki=19时的余数原本就是零。所以由方程组(6)得出方程组(7)有解

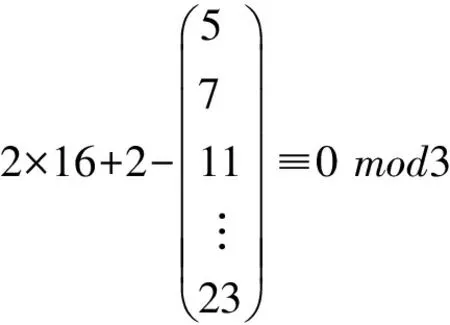
(7)

方程组(7)很显然是无解的——出现矛盾。此时，根据引理1即可得出对于2a=26，定理2成立。

3.2 假设当2a=2n(a≥5，n∈N)时定理1成立

假设当2a=2n(a≥5，n∈N)时定理2成立，同余数表6至少存在一行无零。同时，定理1中方程组(3)和方程组(1)无正整数解。

3.3 递推证明当2a=2(n+1)时定理1也成立

假设当2a=2n(a≥5，n∈N)时定理1成立，递推证明当2a=2(n+1)时定理1也成立，这需要分四种情况讨论，如表7所示[6]。

表6 定理2对应于2n+2的同余数表

表7 数学归纳法向上递推时的四种情况

3.3.1 第Ⅰ种情况

第Ⅰ种情况——2a从2n到2(n+1)没有引起Pk和Pb的变化。根据引理1和解的同步性得知2a=2(n+1)所对应的同余数表至少有一行无零，即方程组(3)无解。故此种情况下，定理1成立。

3.3.2 第Ⅱ种情况

第Ⅱ种情况——2a从2n到2(n+1)没有引起Pb的变化，但是Pk发生了变化。此时，2a=2(n+1)所对应的同余数表比2a=2n时的同余数表(表6)多了一行。根据引理1和解的同步性得知，所对应的同余数表中至少有一行无零，故定理1成立。

3.3.3 第Ⅲ种情况

表8 定理2对应于2(n+1)+2的同余数表

观察表6和表8中的第一行。表6中模的空间是{3,5,7,…,pb}，至少存在一行无零。表8中，行数并没有发生变化，却多了一个模pb+1。只要表8中也至少存在一行无零，则定理2成立。

从表6到表8仍然能够保持定理2成立的两条证明思路是：

(1)反证法

反证法的假设：在表6中模域是{3,5,7,…,pb}时定理2成立，但是在表8中模域是{3,5,7,…,pb,pb+1}时定理2不成立。

反证法的推导：

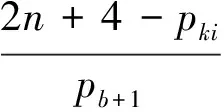
根据“在表8中模域是{3,5,7,…,pb,pb+1}时定理2不成立”的假设，由定理1的方程组(3)得出方程组(8)有解

(8)

因为当y=n+1时，模pb+1的出现仅对pki=3起作用，所以由方程组(8)得出方程组(9)有解

(9)

方程组(9)已经由《采用双无解定理证明哥德巴赫猜想》[4]一文证明是无解的——出现矛盾。故对于2a=2(n+1)，定理2成立。

(2)存在无效列法

查看附表“哥德巴赫猜想的同余数表”可见，附表中的同余数据呈现以3×5×…×pb(模量的积)为周期的横向循环。随着模pb+1的出现，势必能够消除一些在模{3,5,7,…,pb}时的非零余数项，但是消除这些非零余数项的趋势呈现向右下角倾斜的态势，故不可能完全清除以往的非零余数项。模pb+1的出现并不能完全清除以往的非零余数项的原因是模的消去和同余数表横向循环3×5×…×pb的周期不同步。

可以预见：在y≥n+1时，势必会存在许多y的值使得pb+1的出现并不影响y=n时定理2成立。即对于特定的y，如果相对于模pb+1的余数为零时，模{3,5,7,…,pb}的余数原本就是零；如果相对于模pb+1的余数不为零时，模{3,5,7,…,pb}的余数是零或者不是零。这可以通过建立方程组或者借助EXCEL表格进行求解。一旦有特定的y存在，那么根据引理1就可得出定理2成立。

纵观上面两条证明思路，可见第Ⅲ种情况下，定理1成立。

3.3.4 第Ⅳ种情况

3.4 证明结论

根据数学归纳法得出：随着n的递增，定理2所对应的同余数表中至少存在一行无零。定理2成立推出定理1成立。定理1成立，即对一切自然数n(n≥5，n∈N)，哥德巴赫猜想成立。

附表：

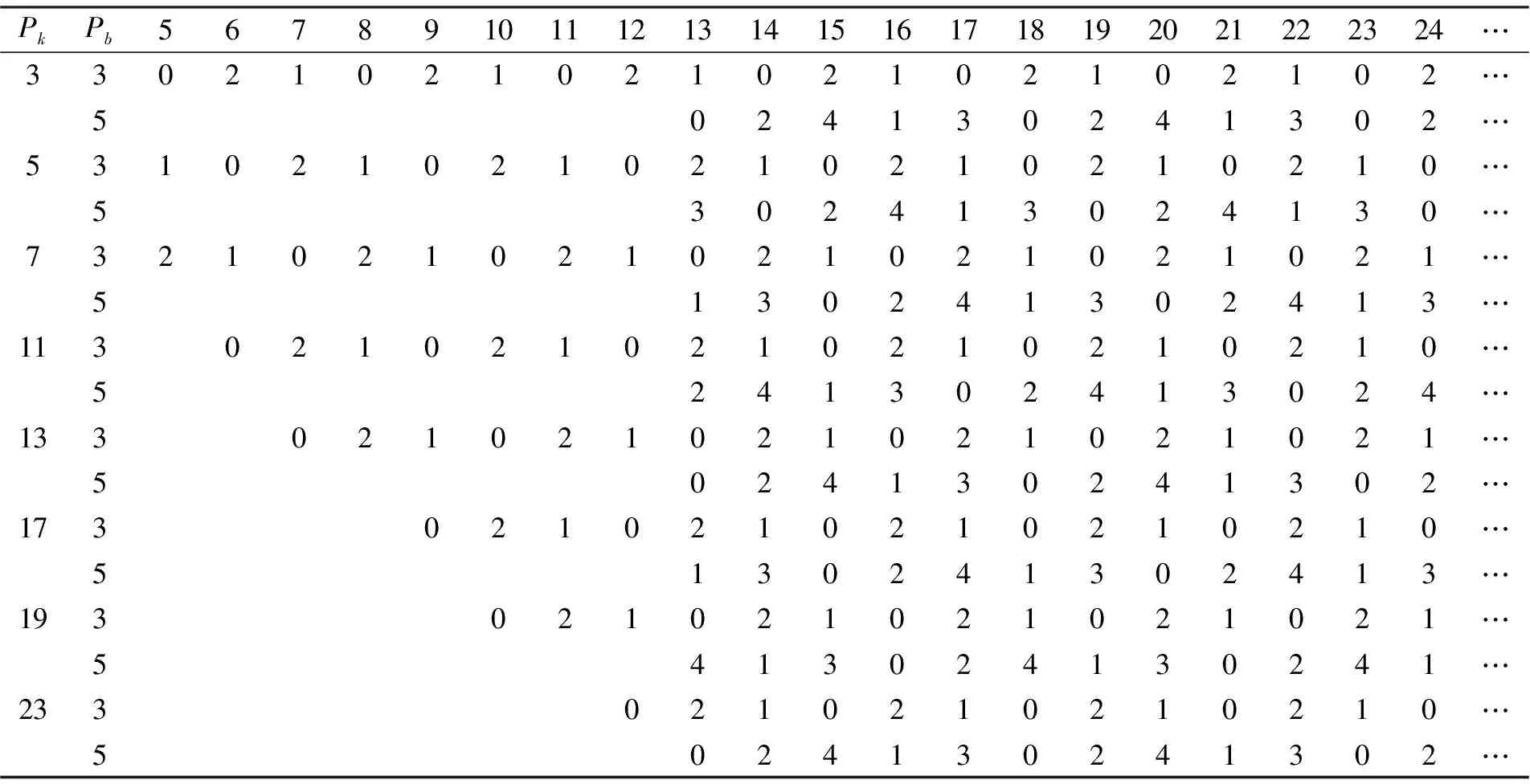
哥德巴赫猜想的同余数表(局部)

注释：

①同余式方程组(1)与《线性代数》或者《矩阵论》上的表示是不同的，这种表示方式也是首创的。这种表示使得(1)同余式方程组左边的常数项得到集中的展示，同时直接表示出了(1)同余式方程组右边的模的集合。

②同余式方程组(2)实质是把Pk以Pb为模进行同模同余表示。如果有方法能够直接证明Pk不能以Pb为模进行同模同余表示，则哥德巴赫猜想迎刃而解。“不能同模同余表示定理”的证明请查阅《用同余数表证明哥德巴赫猜想》一文。

③随着y的递增，表2呈现以3为周期的无限循环延伸，此处只显示y=5、6、7的同余数。

④随着y的递增，表3呈现以3为周期的无限循环延伸，此处只显示y=6、7、8的同余数。

⑤随着y的递增，表4呈现以3为周期的无限循环延伸，请查看y=12、13、14三列及以后的同余数，比较完整。

⑥随着y的递增，表5呈现以3×5为周期的无限循环延伸，请查看y=13、14、…28各列及以后的同余数。

[1] 叶雉鸠.用同余数表证明哥德巴赫猜想[J].长春工程学院学报，2012，(2)：121-125.

[2] 袁明豪.Fibonaeci数列一组模数列的周期[J].黄冈师范学院学报，2007，27(3)：1-3.

[3] 叶雉鸠.采用缺项双无解定理证明哥德巴赫猜想[J].辽东学院学报，2015，(2)：143-149.

[4] 叶雉鸠.采用双无解定理证明哥德巴赫猜想[J].湛江师范学院学报，2012，(6)：17-25.

[5] 叶雉鸠.一类特殊同余方程组解的研究[J].咸阳师范学院学报，2012，(2)：8-10.

[6] 叶雉鸠.哥德巴赫猜想的证明[J].科技信息，2011，(25)：206-207.

责任编辑 王菊平

The double unanswered theorem of Goldbach conjecture and its proof in forms

YE Zhi-jiu

(Shaanxi Technical College of Finance & Economics, Xianyang 712000, Shaanxi， China)

Presents the double unanswered theorem of not lack term about the Goldbach conjecture. If this double unanswered theorem of not lack term unanswered theorem establishment, then the Goldbach conjecture was establishment. This double unanswered theorem of not lack term can be show with congruence forms. The method of recursive proof with the congruence table is more intuitive and there is no suspense. In this paper, we use mathematical induction to prove the Goldbach conjecture.

Goldbach conjecture; the double unanswered theorem of not lack term; congruence forms; mathematical induction

2017-02-20 doi 10.3969/j.issn.1003-8078.2017.03.04

叶雉鸠，男，陕西乾县人，副教授，主要研究方向为数学和经济学研究。

O156.2

A

1003-8078(2017)03-0017-08