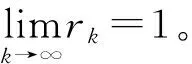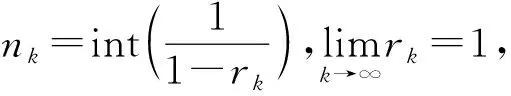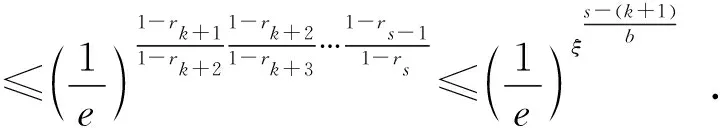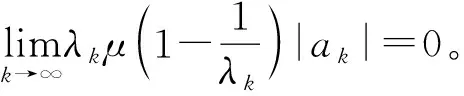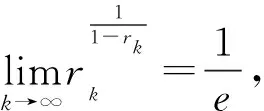Hadamard缺项的μ-Bloch函数的系数特征
杜俊涛
(广东茂名幼儿师范专科学校, 广东 茂名 525000)

如果f∈H(D)满足

在范数‖.‖Bω下,Bω是Banach空间,Bω,0是Bω的闭子空间。当ω(t)=(1-t2)α(α>0)时,Bω与Bω,0即为α-Bloch空间Bα和小α-Bloch空间Bα,0。特别的,当α=1时,Bα和Bα,0即为Bloch空间B和小Bloch空间B0。


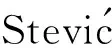

(1)


设μ是权函数,若存在常数0 (2) (3) 则称μ是正规权。 (4) 所以, (5) (6) 并且 |μ*(z)|≤μ*(|z|) . (7) 对任意的r∈[rk0+1,1)⊂[δ,1),取定k>k0,使rk≤r (8) =Cξ,δ,S0ξk=Cμ,λξk. 所以 又由(4)及rk≤r (9) ∀k>p. (10) (11) 注1 由μ*的构造可知,对任意的r∈[ξ,1),存在k使得rk≤r μ(r)μ*(r)≈1,r∈[0,1) . (12) (7)与(12)是正规权的重要性质, 广泛应用于有关函数空间的研究中。 注2 定理A和定理1结合,即得Hadamard缺项级数是由正规权所定义的μ-Bloch函数的充要条件。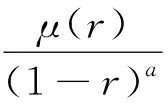

结论与证明