浅谈如何培养中学生的数学逻辑思维能力

广西省河池市巴马县那桃乡初级中学 覃 毅

培养中学生的数学逻辑推理能力，数学教材具有优越的条件。在教学中我们要的是授人以渔，而不是授人以鱼。那究竟怎么样来培养数学逻辑思维能力？为此，有必要作进一步研究。

一、创设数学问题情境，培养学生逻辑推理能力

根据心理学了解，学生的逻辑推理能力并非是自然发生的，而是由学习中碰到需要解决的问题而引起的，在学习中如果没有需要解决的问题，逻辑推理能力就无从发生和进行 。因此，在数学教学中应该根据教学内容与学生情况，精心创设合适的问题情境来诱发学生学习兴趣与求知欲望，从而促进学生的逻辑推理能力的发展。

二、借助几何教学中，培养学生逻辑推理能力

在几何教学中，每一个概念的形成、买一个命题的建立，每一个结论的证明都要经过观察、分析、猜想、判断，再加上科学的论证，时时刻刻都离不开在头脑里合理地进行思维，并且是在不断变化中发展，因此，教学中应鼓励学生摆脱固有的模式，善于从不同角度和方式去思考问题（思维的灵活性），应不满足于停留在表面现象上，引导学生善于概括归类、善于抓住事物的本质的规律、善于遇见事物发展的进程，把思维印象一定的深度和广度（思维的深刻性）。

逻辑推理能力的提高，是一个循序渐进、潜移默化的过程，既不能因为这个种能力的培养是一种长期的任务而放松或者降低对学生的要求，也不能因为其重要性而操之过急，拔苗助长，在几何教学中，阶梯关系的寻找，整体思路的分析、证明方法的优化与评价等，都是训练逻辑推理的好机会，一定要是学生领悟。

三、数形结合，培养中学生数学逻辑推理能力

数形结合的思想，其实质是将抽象的数学语言与直观的图像结合起来，关键是代数问题与图形之间的相互转化，它可以使代数问题几何化，几何问题代数化。数形结合的思想方法包含“以形助数”和“以数辅形”两个方面，其应用大致可以分为两种情形：一是借助形的生动和直观性来阐明数之间的联系，即以形作为手段，数作为目的；二是借助于数的精确性和规范严密性来阐明形的某些属性，即以数作为手段,形作为目的。

（一）用代数方法解决几何问题

函数是数形结合的重要体现。函数思想，是指利用函数的概念和性质去分析问题和解决问题。有时，还实现函数与方程的互相转化、接轨，达到解决问题的目的。

如图，小刚的爸爸从市场上购买一块矩形铁皮，他将此矩形铁皮的四个角各剪去一个边长为1米的正方形后，剩下的部分刚好能围成一个容积为24立方米的无盖长方体合子，且此长方体合子的底面长比宽多2米，现已知购买这种铁皮每平方米需15元钱，问小刚的爸爸购买这张矩形铁皮共花了多少元钱？

分析：本题考查了列一元二次方程解决实际问题。设盒子底部宽为x米，则长为(x＋2)米，根据长方体的体积公式：长×宽×高，进而列方程，再计算矩形铁皮的面积，从而可求得购买这张矩形铁的价值。

解：设合子底部宽为x米，则长为(x＋2)米，

依题意，得：x(x＋2)·1＝24

解之得：x1＝－6（舍），x2＝4

∴ 合子底部宽为4米、长为4＋2＝6米。

由长方体展开图知，矩形铁皮面积为：(6＋2)×(4＋2)＝48平方米

∴ 做一个这样的合子要花48×15＝720元。

利用方程思想来解决几何问题，是从问题的数量关系入手，运用数学语言将问题中的条件转化为等式或是不等式，然后通过解方程(组)或不等式(组)来使问题得到解决。

值得注意的是：方程是解决问题的重要工具，列方程解应用题都应注意求出的未知数的值是否符合题意，即检验，应舍去不合题意的未知数的值，这类试题重在培养学生应用数学解决实际实际问题的意识，解题谨慎，步步深入，有助学生培养逻辑推理能力。

（二）用几何方法解决代数问题

数与形在一定条件下是可以互相转化的，某些代数问题往往有几何背影，而借助其背影图形的性质，可以使那些抽象的概念、复杂的数量关系变得直观。在解决数量有关的问题时，根据数量的结构特征，构造出相应的几何图形，转化为几何问题，从而便于探求解题思路，找到解决问题的捷径。

例2：已知x、y为负数，z为正数，且|y|＞|x|＞|z|，

化简：

分析：根据题意，画出数轴，从数轴上很明显的可以看出这三个数的大小，然后根据“两个数之差的绝对值，去掉绝对值后，用大的数减去小的数”的方法进行化简。

解：根据题意，画出数轴：

由数轴可知：z＞x＞y，则有

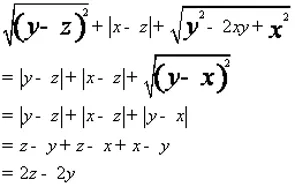
以上例题说明了有关“数”方面的问题，借用“形”的性质之后，可以使许多抽象的关系直观化，形象化和简单化，也有助于对问题的内在联系更进一步的了解，从而变难为易，化繁为简。借助数形结合的方法，对培养学生的逻辑推理能力有很大的帮助。

总而言之，提出问题并解决问题是推动数学发展的动力。而数形结合是解决数学问题的一个有力工具，也是培养学生逻辑推理能力的重要方法之一。在数学教学中，要注重培养我们的学生能恰当地利用数形结合思想提高解题效率，提高学生的成绩。

本文主要从几何教学和数形结合两方面来研究，然而，有多种渠道多种方法可以培养学生的逻辑推理能力。只要我们掌握了一定的基础知识，并能够注意观察审题，准确找到题目中的解题信息，然后进行综合分析，形成正确的逻辑思维就是很自然而然的的事情。当然在教学中培养学生的逻辑思维能力除了在一些方法上和技巧上加强训练外，还应多启发学生多想、多练、多问，并开展多种形式的讨论，这有利于培养学生进行逻辑思维的习惯。只有注意培养数学逻辑思维能力，才能在解数学综合题中做到“游刃有余”。随着教育改革的不断深入，更要重视学生综合能力的培养，数学教育只有使学生在思维能力、情感态度与价值观等方面得到提高和发展。才能学到数学的精髓，只有这样，我们才能真正做到“授人以渔”而不是“授人以鱼”。

本研究存在很多不足之处，比如，在学生的兴趣爱好、教学环境等也对培养逻辑推理能力有着很大的影响，都没能进一步深刻的讨论。在写作过程中，我深深认识到自己才疏学浅，对一些知识点掌握还不够扎实，在语言组织能力还有待提高。