探究数学课堂教学中负迁移现象

福建省仙游县鲤南中心小学 黄国枢

分析学生在数学某些基础知识和掌握基本技能中所出现的错误时，往往会发现有许多错误是相同的或相类似的。这说明学生已有的知识技能对新知识、新技能的形成和掌握产生了干扰，这种现象在心理学上叫负迁移。心理学研究表明，学习上的负迁移是可以防止和消除的。因此，探索研究小学生在学习教学中负迁移的表现和心理原因，从而在教学中采取针对性的对策，防止和消除旧知识对学习新知识的干扰，对全面提高课堂教学质量是很有探究意义的。

一、负迁移的主要表现及其产生的原因

（一）新、旧知识有相似或相近的地方，学生往往混淆不清，产生学习上的负迁移

新、旧知识既有联系又有区别，乍看起来差不多，学生往往只注意它们之间的联系，而忽视它们之间的本质区别，容易产生混淆现象，引发错误的联想，得到错误的结论。如：学生学过偶数、奇数概念后，再学习质数、合数时，常常误以为很多合数能被2整除，就认为合数就是偶数，又因为除了2以外的质数不能被2整除，就认为质数就是奇数等。

（二）旧知识的定势作用，干扰新知识的学习和运用，产生了学习上的负迁移

例如，初学“同分母分数加减法”时，会经常出现分子相加减和分母相加减的错误。产生这类错误的原因，主要是整数加减法的定势干扰，因为整数加减法多次再现，认识和应用整数加减法知识的定势较强，同分母分数加减法学生却刚刚接触，认识和应用同分母分数加减法知识的定势较弱。于是，整数加减法的定势对同分母分数加减法的学习产生负迁移，出现了分子相加减、分母相加减的错误。

（三）缺乏良好的学习习惯，特别是缺乏良好的审题习惯，产生了学习上的负迁移

如解答“小红有12本图书，比小青少4本，小青有多少本图书？”这类问题时，学生若不认真分析“谁的本数与谁的本数比，谁的本数多，谁的本数少”，见到“少“就用减法算，就会容易产生错误。

另外，遇到“日常概念”和“数学概念”的名称相同，而本质不同时，学生往往用日常概念替代数学概念。如日常生活中“边”和“棱”是不分的，学生学习长、正方体时，往往把“棱”叫做“边”；又如，日常生活中高的概念，一般是与水平成垂直的直线，对下图中的线段a，学生往往不认为它是三角形的高。

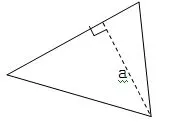
二、有效地防止和消除学生学习中的负迁移对策

（一）加强基础知识教学，帮助学生掌握知识的本质

例如，教学上图中“三角形的高”，应结合图例，着重使学生懂得：三角形的任何一条边都可以看作三角形的底，确定某一条边作为底，那么从这条边对角的顶点向这条边作一条垂线，顶点和垂足之间的线段就是三角形的高。在直角三角形中，如果以一条直角边作为底边，那么另一条直角边就是直角三角形的高。这样，就可以纠正学生的错误概念，即三角形只有成水平的这一条边才叫做底，和这个垂直的直线才是高。

又如，学生学习整数加减时，如果只停留在“末位对齐”的水平上，因整数中末位就是个位，数位对齐是一致的，学生把二者就等同起来，于是学习小数加减时常常出现如下错误：

如果在讲解整数加减法时,突出计算法则的本质：相同数位上的数才能相加减，“数位对齐”就是相同数位上的数相对齐。这样，整数加减法的计算法则不但不会干扰小数加减法的学习，相反还会促进小数加减法的学习，更进一步明白新旧知识的内在联系。

（二）重视新旧知识的比较，提高学生的鉴别能力

在很多情况下，旧知识对于新知识的干扰是由于旧知识和新知识相似或相近而产生的。因此进行比较，提高学生的鉴别能力，弄清新旧知识的联系和区别，有利于防止和消除旧知识对新知识的负迁移。

比较，要抓住新旧知识的本质区别进行。例如，“整除”中的“倍数”与除法中的“倍”这两个概念的本质区别是：1.“倍数”表示两个数的关系，不是一个值，而除法中的“倍”是一值。如12是4的倍数，表示12与4的关系；12÷4=3表示12是4的3倍；2.一个数是另一个数的倍数，是以一个数能被另一个数整除为前提的；除法中的“倍”则不一定。教学中，如果我们能抓住上述本质区别进行比较，不但能帮助学生弄清这两个概念的区别，而且加深了学生对“倍数”的理解。

比较，要从多角度进行，使学生全面掌握新旧知识的区别。例如，学生常常把平面图形的周长和面积互相混淆，为了区别它们，我从它们的意义、计算公式和使用的单位几个方面进行比较，并列成如下表格：

名称 意义 计算公式 单位面积 圆所围平面部分的大小S=πr2 面 积 单位周长 圆一周的长度 C=π d或C=2πr长度单位

这样，学生对面积、周长知识的理解和运用就不易混淆了。

（三）精心设计练习，防止和消除负迁移

实践证明，旧知识对于新知识的负迁移，与新知识的巩固程度密切相关，新知识越巩固，旧知识对它的干扰就越小。因此，数学中可以通过有计划的练习，防止和消除旧知识对新知识的干扰。

设计练习题时要注意以下几个方面：目的明确，重点突出，克服盲目性；练习题的编排要有阶段性、由易到难，由基本题到综合题；要进行对比练习，防止混淆，弄清联系，练习的形式要多样，以提高学生的应变能力。

此外，还要视班级情况，注重培养学生良好的学习习惯，特别是认真审题的习惯，做到解题前先复习有关基础知识，再做练习题；解题时，先认真审题，弄清题目的条件和问题，正确理解题中的关键词语，分析数量关系；解题后，要进行检验等。