《相似三角形的判定(1)》教学设计
山东省宁阳第二实验中学 刘艳菊
一、教材分析
本节学习内容是《相似三角形的判定》,它是在学生学习了全等三角形的性质和判定方法和相似三角形的概念基础上,通过类比的方法进一步研究三角形相似的条件,同时本节内容也是研究其他判定定理的基础。
二、教学目标
知识与技能:1.初步掌握两角对应相等的两个三角形相似的判定方法,并且能够运用它们进行简单的证明及计算
2.通过习题的引申练习,培养学生解决问题的能力
过程与方法:经历相似三角形与全等三角形的类比过程,进一步体验类比思想、特殊与一般的辨证思想
情感态度与价值观:积极参与数学活动,体验数学活动充满探索与创造,形成实事求是的态度及独立思考的习惯
三、教学重点及难点
重点 相似三角形判定定理(1)
难点 能正确运用判定定理(1)解决数学问题。
四、教学方法与手段
1.教学方法:直观演示验证法自主、合作、探究式
2.教学手段:借助于多媒体课件演示及学生动手操作确认发现新知。
五、教学过程
【创设情提出问题境】(学生回答)
【板书课题】 《相似三角形的判定(1)》
【自主探究,感受新知】(1、学生亲手实践2、学生理解3、边听讲边思考)
1.教师活动:一个角对应相等的两个三角形是否一定相似?
学生活动:画图试试看(每人画一个ΔABC,使得∠BAC=60°,看所画的三角形是否相似。)
2.教师活动: 两个角对应相等的两个三角形相似吗?
学生活动: 完成课本40页实验与探究。
3.教师活动 如果两个三角形有若干个角对应相等,那么至少有几个角对应相等就能保证这两个三角形相似?
学生活动: 小组合作交流,共同探究,得出结论
4.教师活动 由以上问题,我们可以得到结论:__________________________________。
5.学生活动:如右图,结合图形用数学符号语言表示:
∵∠ A= ∠ A’,∠ B= ∠ B’
∴△ABC ∽____________。
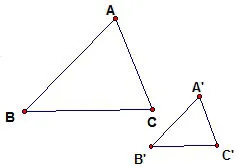
(让学生通过亲手实践来体验知识的准确性,理解,消化主要知识)
【尝试练习】
例1:已知:ΔABC和ΔDEF中,∠A=40°,
∠B=8 0°,∠E=8 0°,∠F=60°,
求证:ΔABC∽ΔDEF.
学生活动: 分小组交流后个别回答 ,探索证明方法
(鼓励学生用自己的语言说明理由,并逐步渗透用数学语言进行说理的能力)
例2:课本41页例1,画出图形并写出解题过程.
学生活动:小组合作交流,共同探究,得出结论
【巩固训练】
学生活动 思考,实践,理解,让学生通过亲手实践来体验知识的准确性,
理解,消化主要知识
1.下列三角形中哪些是相似的?
2.已知:如图,在△ABC中,点D、E分别在AB、AC上,且∠1=∠B
(1)求证:△ADE∽ △ABC
(2)若∠A=50°,∠C=70°,求∠1的度数
(3)若AE=2,BE=3,AC=4,求AD的长
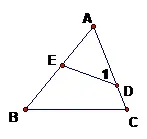
【挑战自我】.完成课本41页挑战自我,写出解答过程。
【课时小结】
教师活动 通过这节课的学习,你能获得哪些收获?也可以对本堂课进行质疑。
学生活动 分小组交流后个别回答,使知识系统化
(1)知识上的收获(2)数学思想方法的领悟(3)能力上的提高
(4)谈谈学习过程的体验和感受
【当堂测试 】 学生活动
1.判断题:
(1)两个顶角相等的等腰三角形是相似的三角形. ( )
(2)两个等腰直角三角形是相似三角形. ( )
(3)底角相等的两个等腰三角形是相似三角形. ( )
(4)两个直角三角形一定是相似三角形. ( )
(5)一个钝角三角形和一个锐角三角形有可能相似. ( )
(6)有一个角相等的两个直角三角形是相似三角形. ( )
(7)有一个锐角相等的两个直角三角形是相似三角形. ( )
(8)连接三角形的三边中点所围成的三角形与原三角形相似.( )
(9)所有的正三角形都相似.( )
(10)两个等腰三角形只要有一个角对应相等就相似. ( )
2.填空:(填上“不”、“不一定”或“一定” )
两个等腰三角形都有一个角为45°,这两个等腰三角形_______相似;如果都有一个角为95°,这两个等腰三角形_______相似.
3.已知△ABC如右图,则下列4个三角形中,与△ABC相似的是()
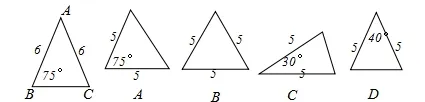
4.小明正在攀登一个如图所示的攀登架,DE和BC是两根互相平行的固定架,DE=10m,BC=18m,小明从底部固定点B开始攀登,攀行8m,遇上第二个固定点D,小明再攀行多少米就可以到达这个攀登架的顶部A?

【拓展隧道】学生活动
如图,点C、D在线段AB上,且ΔPCD是等边三角形.
(1)当AC,CD,DB满足怎样的关系时,ΔACP∽ΔPDB;
(2)当ΔPDB∽ΔACP时,试求∠APB的度数.
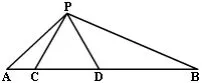
教师活动 【作业布置】: 必做题:A组1、2
选做题: B组1、 完成本节配套练习册
预习: 《相似三角形的判定(2)》
【教学反思】
本节课主要是探究两个三角形相似的判定方法,因此在教学设计中突出了探究的过程,从而给学生以深刻的数学学习体验。通过基本图形的训练,引导学生学习要抓实质,学会把复杂的问题简单化的方法,并且结合图示,训练学生语言表达能力。同时组织好小组合作学习,加强师生之间的互动,培养学生在独立思考问题的基础上,能够理解他人的意见,并学会与他人合作的能力。

