浅谈函数“恒成立问题”与“最值问题”的等价转化

福建省连城一中 张涛生

纵观近10年全国卷高考数学压轴题，基本体现以下三个方面的基本关系。

（一）各类不等式与函数最值的关系，如下表。

不等式类型 与最值的关系

?

（二）函数f(x)对区间D的x1、x2，都有恒成立，

3、已知f(x)对总存在对于使得设f(x)在区间D1上的值域为A，g(x)在D2上的值域为B，则A⊆B.

主要有以下三方面的题型。

一、与三角形构建有关的“恒成立问题”

例1，已知若 在区间[0，2]上任取三个数a、b、c，均存在着f(a)、f(b)、f(c)为边长的三角形，求实数m的取值范围。

解：

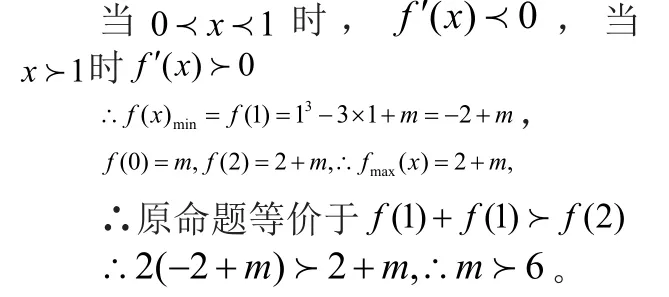
[命题意图]：把“三角形存在性问题”转化任意的两边之和大于第三边，转化为两条最小边之和大于最大边。

二、与不等式有关的“恒成立问题”

例2，已知函数（x）+g（x）.若关于x的不等式F（x）≤mx-1恒成立，求整数m的最小值；

解：令

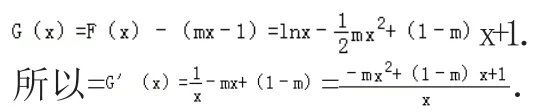
当m≤0时，因为x＞0，所以G′（x）＞0所以G（x）在（0，+∞）上是递增函数，

又因为G

所以关于x的不等式G（x）≤mx-1不能恒成立.

当m＞0时.

令G′所以当时，G′（x）＞0；当时，G′（x）＜0.

因此函数G（x）在是增函数，在是减函数.

故函数G（x）最大值为.

令h （m）=因为h（1）h（2）

又因为h（m）在m∈（0，+∞）上是减函数，所以当m≥2时，h（m）＜0.

所以整数m的最小值为2.

[解题思路]：利用计算函数在区间D的最大值和最小值解决函数的恒成立问题。

例3，如果函数满足对任意的都有恒成立，则实数a的取值范围是？

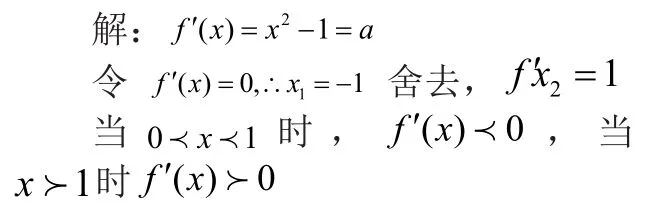
三、与等式有关的“恒成立问题”

例4，已知

（Ⅰ）求的单调区间；

（Ⅱ）若对任意的总存在使求实数a的取值范围.

解：设在区间[1,e]上f(x)的值域为A，在[0,3]上g(x)的值域为B，

则依题意A⊆B易知g(x)在[0,1]上递增，在[1,3]上递减，

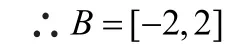
①当a≤0时，f(x)在[1,e]上单调递增，

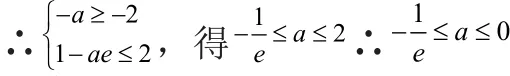
②当a≥1时，f(x)在[1,e]上单调递减，A = [1 - ae,- a]

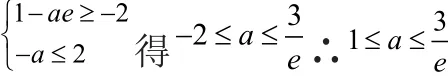
③当时，f(x)在[1,e]上单调递增，可得

④当时，f(x)在[1,e]上

综上，实数a的取值范围为

以上这些例题中，本质问题就是构造函数，把问题转化为函数的最大（小）值，进而研究函数在区间D上的最值，通过求导，得出极值点的坐标，从而得出函数的最大（小）值，确定参数的取值范围，这是这类问题的基本解题思想。