基于Bezier曲面四边形边界元法的特高压绝缘子串电场计算

李亚莎,花 旭,沈星如,代亚平

(三峡大学 电气与新能源学院，湖北 宜昌 443002)



基于Bezier曲面四边形边界元法的特高压绝缘子串电场计算

李亚莎,花 旭,沈星如,代亚平

(三峡大学 电气与新能源学院，湖北 宜昌 443002)

在三维静电场的边界元计算中，为了快速、精确计算电位和电场强度分布，提出了用双2次Bezier曲面四边形拟合实际积分面的Bezier曲面四边形边界元方法。该方法利用二阶剖分单元的节点坐标信息来构造双2次Bezier曲面参数方程，再利用Bezier曲面参数方程和面积比值法构造对应于Bezier曲面4个顶点节点的形状函数；以Bezier曲面4个顶点节点为计算节点，大大减少了计算节点数；与一阶平面四边形边界元法相比，双2次Bezier曲面能够更好地拟合实际积分面，提高计算精度。并且可通过精细后处理技术将模型表面的函数值精细显示。算例结果表明，Bezier曲面四边形边界元法与传统边界元法相比，在网格剖分节点数相同时，计算精度得到了提高。在计算精度相同条件下，该方法中的节点数量降低，减少了计算机内存的使用。最后，将Bezier曲面四边形边界元法应用于交流特高压绝缘子串电场的计算。

静电场计算；Bernstein基函数；Bezier曲面；边界元法；精细后处理

0 引 言

随着电力系统电压等级的提高，对高压电力设备的绝缘性和安全性提出了严峻挑战。在三维电场中，电位和电场强度分布的快速、精确计算对高压设备的结构设计和绝缘保护具有重要指导作用。而这类计算问题属于开域电场问题。在电磁场数值计算中，截断法[1]、有限元法[2，3]、边界元法[4，5]和有限元-边界元耦合法[6，7]是处理开域问题的常用方法。其中，边界元法产生的网格单元数少，计算速度快，是计算开域问题的理想方法[8-11]。

在传统边界元法中，通常采用平面三角形或四边形作为剖分单元[12]。但面对复杂的场域边界面，平面单元拟合实际边界的效果较差，增大了积分区域产生的误差，降低了计算精度。为了使剖分单元构成的边界面与求解区域的边界面足够近似，需对网格尺寸足够细化。剖分尺寸越细，拟合度越高，在剖分单元上的积分误差也越小。这样做显然会增加计算节点数，导致计算量加大。若采用二阶插值单元，可以提高计算精度，但同时增加了节点数量，使计算速度明显降低[13]。因此，采用二阶插值单元并没有解决边界元法中求解自由度和计算精度之间的矛盾。

目前在复杂的三维静电场计算中，计算机内存的占用仍是制约方程组求解的关键因素。为了减少计算机内存的使用，加快计算速度，同时提高计算精度。本文提出Bezier曲面四边形边界元方法，可以在单元剖分比较粗糙的情况下保证较高的计算精度，有效降低求解自由度的数量，解决边界元法中求解自由度与计算精度之间的矛盾。最后通过精细后处理技术将边界面及其上面函数值的分布精细显示出来。

1 Bezier曲面四边形边界元原理

1.1 Bezier曲面理论基础

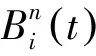
(1)

Bezier曲面参数方程S(u,v)定义为

(2)

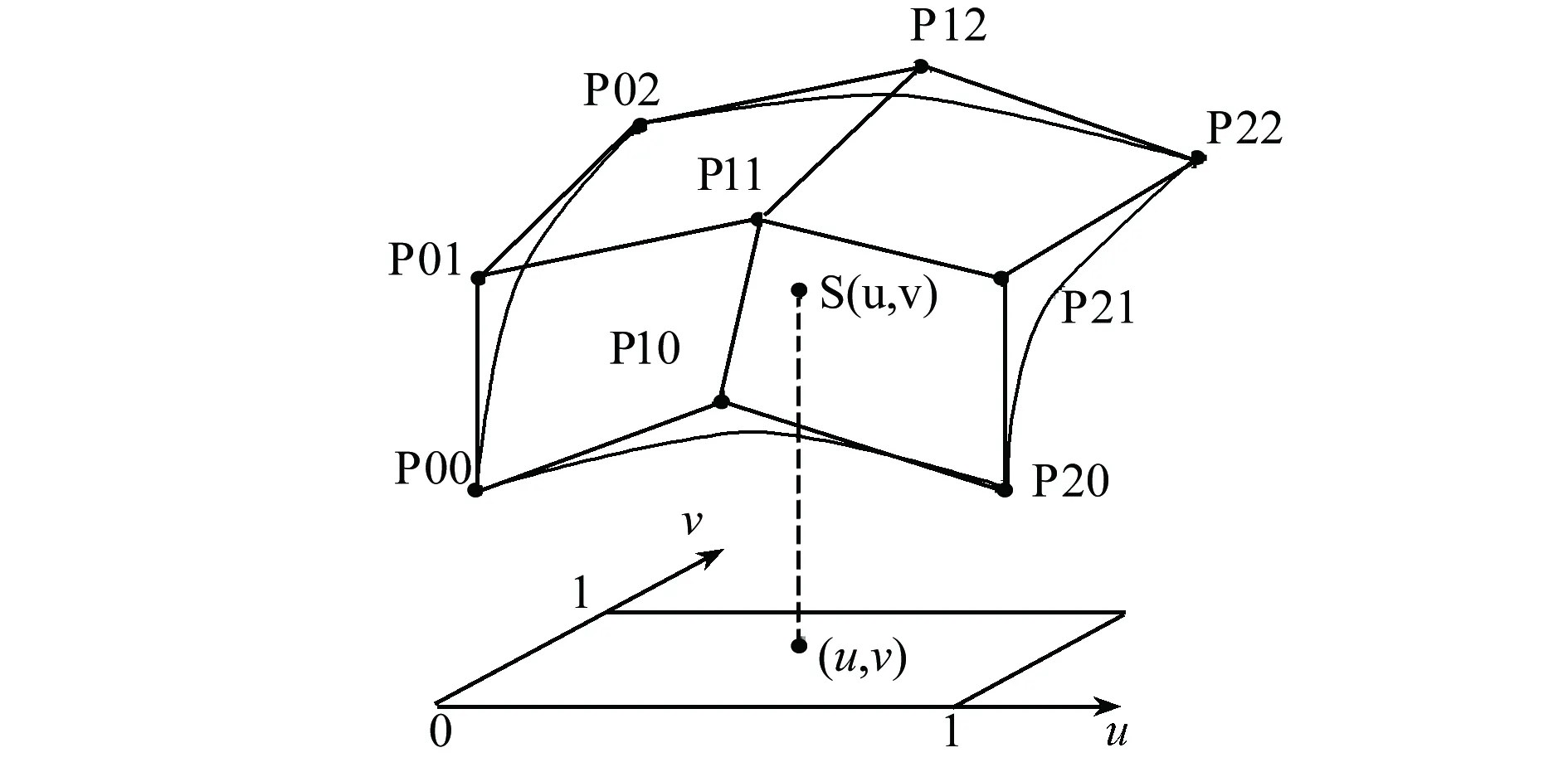
图1 双2次Bezier曲面及控制网格Fig.1 Double quadric Bezier surface and its control grid

式中：Pij为Bezier曲面的控制顶点。把同行和同列中相邻的两个控制顶点用线段相连所得到的m×n边折线网络称为Bezier网[15]，如图1所示。

1.2 双2次Bezier曲面四边形的构造

由参数方程组(2)的定义可知，双2次Bezier曲面四边形须由2次Bernstein基函数以及控制顶点来构造。2次Bernstein基函数如式(3)所示：

(3)

构成二阶四边形单元的节点数有8个。其中4个顶点节点记为Q00，Q20，Q22，Q02，另外4个边中节点记为Q10，Q21，Q12，Q01。利用二阶四边形剖分单元的形状函数和这8个节点的坐标值进行插值，求得中心点Q11的坐标值。将所拟合的Bezier曲面上9个节点的坐标值代入参数方程(2)，并将式(3)代入，得到：

(4)

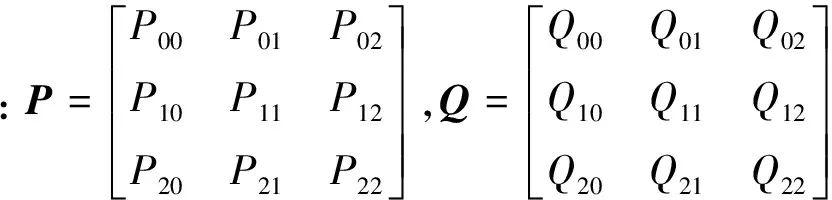
1.3 Bezier曲面四边形单元上的形状函数

以Bezier曲面四边形的4个顶点作为计算点，需要构造对应于这4个顶点的形状函数[16]。如图2所示，取双2次Bezier曲面四边形上任意一点作为细分点，将Bezier曲面四边形单元细分为4份，用高斯积分求出这一点对应顶点1，2，3，4的小单元面积A1，A2，A3，A4，定义这一点对应顶点1，2，3，4的形状函数为

(5)

其中A为曲面总面积，A=A1+A2+A3+A4。

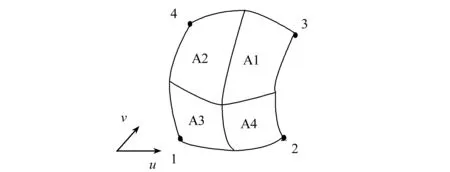
图2 曲面细分Fig.2 Surface subdivision

1.4 Bezier曲面四边形边界元方程

三维静电场的边界积分方程为

(6)

应用伽辽金加权余量法[17]对式(6)进行离散可得

(7)

式中:e′和Se′分别表示源单元编号和源单元积分区域；e和Se分别表示场单元编号和场单元积分区域；Nj为相应的权函数；Ni为相应的Bezier曲面四边形的形状函数。

1.5 Bezier曲面四边形精细后处理

Bezier曲面四边形单元上任意点的坐标可由曲面参数方程(2)确定。在Bezier曲面参数方程中，按照一定的步长增加曲面上两个参数的值，所形成的等参数线将Bezier曲面四边形划分为许多网格。将所划分的网格和结点作为新的单元和节点，依照Bezier曲面参数的改变进行重新编号，便可精确显示出Bezier曲面四边形单元。利用Bezier曲面四边形单元上的形状函数和顶点节点函数值计算出所有新编节点上的函数值，便可精细显示曲面单元上的函数值变化。

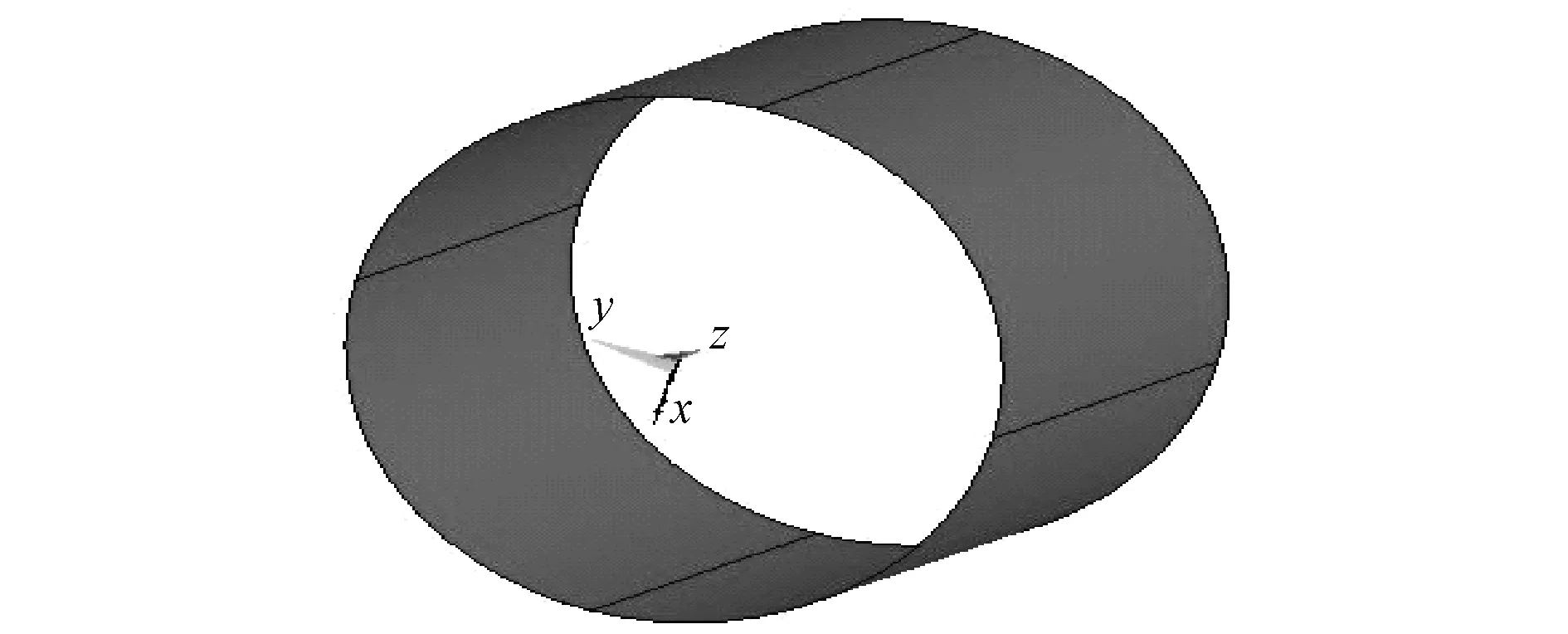
图3 圆柱面Fig.3 Cylindrical surface

2 算 例

2.1 曲面拟合误差

如图3所示，取一底半径为1，高为2的圆柱侧表面。将侧表面规则剖分为四个单元，用传统边界元法计算其中一个单元的面积为2.828 4，与实际面积的相对误差为9.97%。用Bezier曲面四边形边界元法计算同一单元的面积为3.135 3，与实际面积的相对误差为0.2%。可以看出Bezier曲面四边形拟合精度更高。

2.2 单个球形电极表面的电场强度分布

加100 V电压于一个导体小球，若球半径为1 m，则球面上的电场强度为100 V/m。将球面剖分成106个单元。用Bezier曲面四边形边界元法和一阶平面四边形边界元法分别计算球面上108个节点的电场强度。得出电场强度随θ角的分布如图4所示。

从图中可以算出，一阶平面四边形边界元产生的最大相对误差为6.2%。而Bezier曲面四边形边界元最大相对误差为0.83%。且计算结果分布较为集中。由此可以得出，在相同剖分节点数的情况下，Bezier曲面四边形边界元法的计算精度高于传统边界元法。

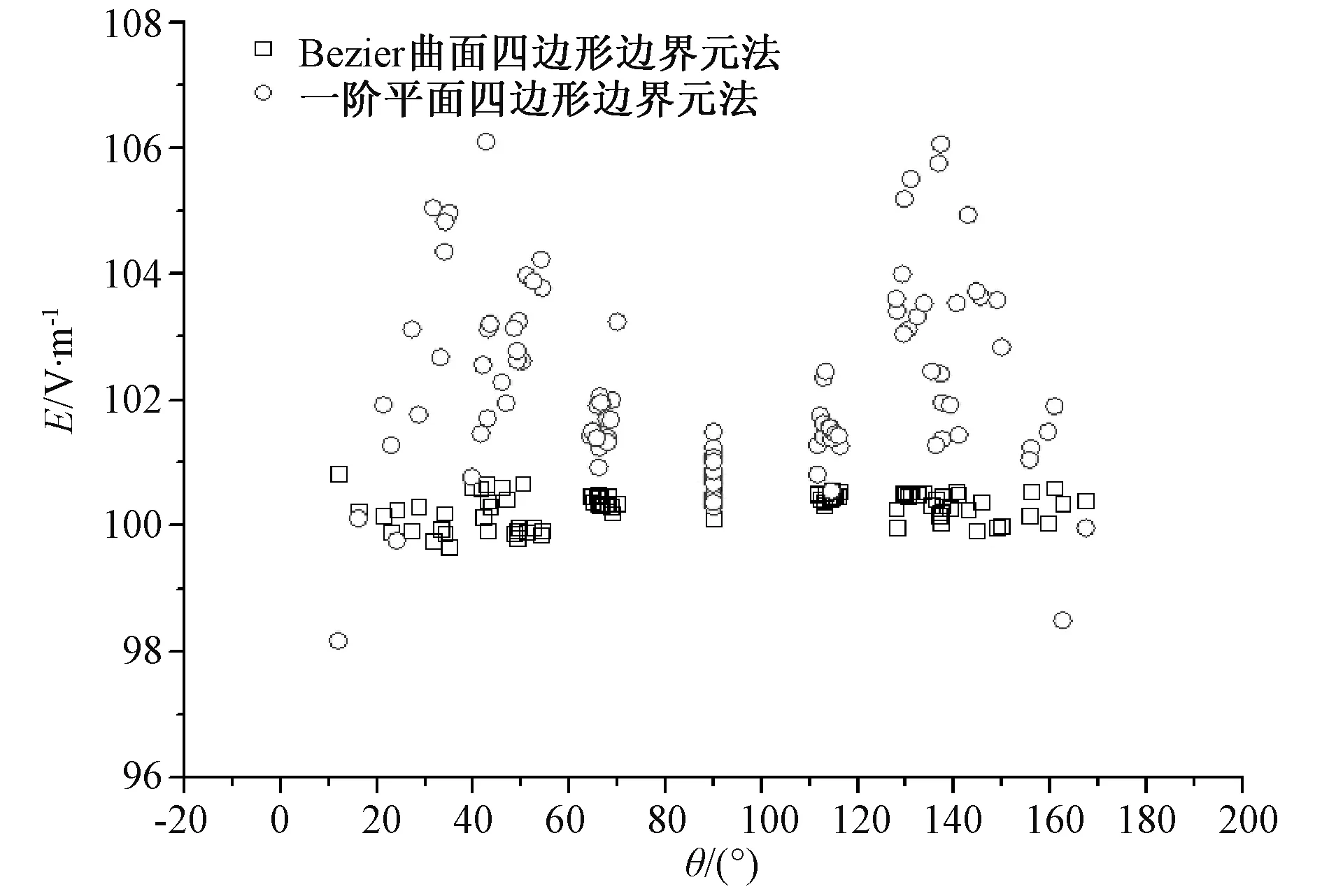
图4 导体球表面电场强度沿球面θ角分布Fig.4 Distribution of electric field intensities vs. θ on surface of sphere

2.3 柱形孤立电极表面电场强度精细后处理

图5 柱形电极精细处理前后电场强度云图Fig.5 Cylindrical electrode electric field strength distribution

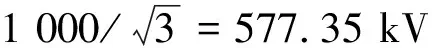
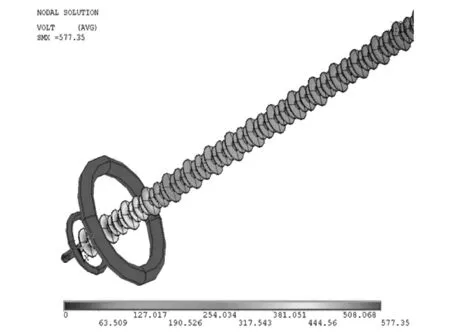
图6 特高压交流绝缘子串电位云图Fig.6 UHV AC insulator string electric potential distribution

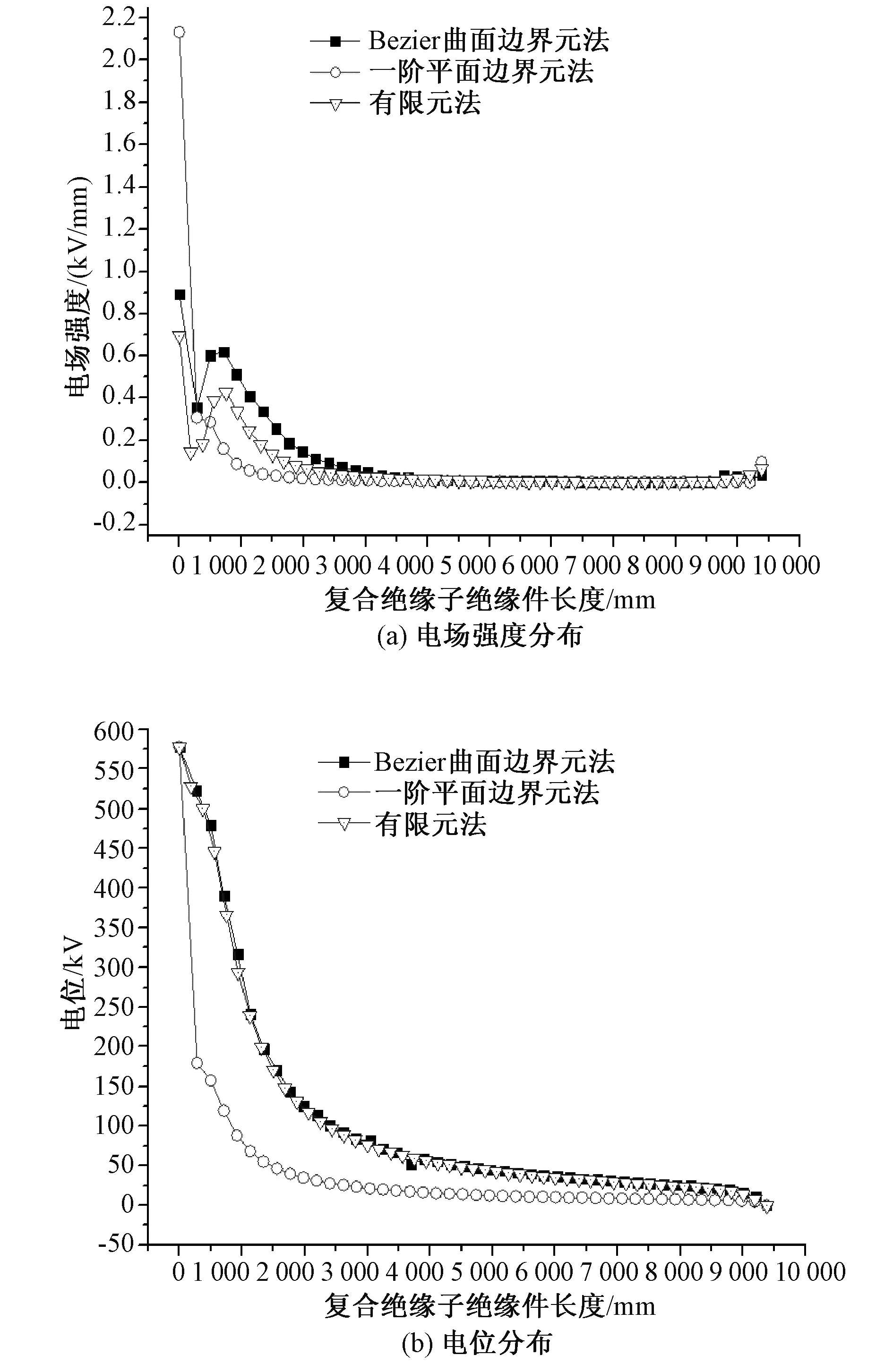
图7 特高压交流绝缘子串表面电场强度和电位分布Fig.7 UHV AC insulator strings electric field strength and potential distribution

图6是利用Bezier曲面参数方程及曲面上的插值函数精细后处理的电位分布结果。为了便于比较Bezier曲面四边形边界元方法的计算精度，图7(a)和图7(b)中同时给出了二维轴对称场有限元计算结果和一阶线性单元边界元计算结果。由图7(a)可以看出，在高压端，Bezier曲面四边形边界元法计算结果比有限元结果略偏高，但数值差别不大，二者电场强度分布趋势是一致的，而一阶线性边界元在高压端的结果先偏大后偏小，并且分布趋势与前两者也不一致。由于有限元法采用二维轴对称场计算方法，且剖分比较密，计算结果相对比较准确。以有限元法计算结果为基准，可以看出，在剖分相同，计算节点数相同的条件下，Bezier曲面四边形边界元法计算精度明显高于一阶线性边界元。图7(b)给出了沿绝缘子串的电位分布，Bezier曲面四边形边界元法计算结果与有限元计算结果基本一致，而一阶线性边界元计算结果则误差相对较大。从图7(b)的电位分布可以看出，当复合绝缘子串长度距高压端3 000mm以上时，Bezier曲面边界元法、一阶平面边界元法和有限元法的电位曲线斜率基本趋于一致。由于电位曲线的斜率就是电场强度，因此在图7(a)中3种方法计算的电场强度在远离高压端计算结果基本趋于一致。

2.5 特高压双绝缘子串电场分布

Bezier曲面四边形边界元法不仅能应用于轴对称模型，还可应用于更加复杂的大型三维静电场计算模型。建立特高压双绝缘子串模型，两者相距400 mm，并在高低压端平行放置两个相同大小的跑道型均压环，环中心径设为195 mm，管径为50 mm，联结距为600 mm。分别对高压侧和低压侧施加577.35 kV和0电位，图8所示为特高压交流双复合绝缘子串上的电位云图。为了验证Bezier曲面四边形边界元法的有效性和准确性，建立三维有限元模型，采用二阶单元高密度剖分。图9所示为特高压绝缘子串沿面电位分布图，从图9可以看出Bezier曲面边界元法与有限元法的计算结果几乎保持一致，从而验证了该方法的有效性和准确性。

图 8 特高压交流双绝缘子串电位云图Fig.8 UHV AC double insulator strings electric potential ditribution

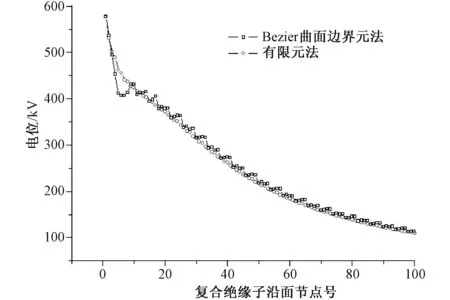
图9 特高压交流双绝缘子串表面电位分布Fig.9 UHV AC double insulator strings electric potential ditribution

3 结 论

(1)本文提出了Bezier曲面四边形边界元方法。该方法与一阶线性四边形边界元相比，边界曲面的拟合精度有显著提高。算例的计算结果表明，在网格剖分和计算节点数相同的情况下，Bezier曲面四边形边界元法比线性单元边界元法计算精度有显著提高。在计算精度要求相同的情况下，采用Bezier曲面四边形单元，可降低节点数量，减少对计算机内存的占用。Bezier曲面四边形边界元法有效解决了边界元法中求解自由度和计算精度间的矛盾。

(2)Bezier曲面四边形边界元法可通过精细后处理技术将单元以及单元上各点处的函数值精细显示。算例结果表明，通过精细后处理的求解区域边界面与实际边界更加逼近，且能详细反映函数值在整个边界面上的变化规律。

[1] 刘守豹, 阮江军, 杜志叶, 等. 有限元—边界元耦合法在3维开域涡流场中的应用[J]. 高电压技术, 2010, 36(3):655-660.

[2] 高俊国, 于平澜, 李紫云, 等. 基于有限元法的电缆金属护套感应电压仿真分析[J]. 高电压技术, 2014, 40(3):714-720.

[3] 赵志刚, 李光范, 李金忠, 等. 基于有限元法的大型电力变压器抗短路能力分析[J].高电压技术, 2014, 40(10):3214-3220.

[4] 梁曦东, 李雨佳, 张轶博, 等. 输电导线的覆冰时变仿真模型[J]. 高电压技术, 2014, 40(2):336-343.

[5] CHIAMPI M, ZILBERTI L. Induction of electric field in human bodies moving near MRI：an efficient BEM computational procedure[J]. IEEE Transactions on biomedical engineering, 2011, 58(10)：2787-2793.

[6] 黄道春, 阮江军, 刘守豹. 特高压交流复合绝缘子电位和均压环表面电场分布计算[J]. 高电压技术, 2010, 36(6):1442-1447.

[7] 谢裕清, 李琳. 计算多介质电场节点场强的有限元-边界元法[J]. 华北电力大学学报(自然科学版), 2016, 43(4):21-26.

[8] 刘士利, 王泽忠, 孙超. 应用伽辽金边界元法的直流换流站屏蔽罩表面场强计算[J]. 电网技术, 2011, 35(5)：223-227.

[9] 李世琼. 开域电磁场全源积分人工边界方法[D]. 北京：华北电力大学,2015.

[10] 刘姜玲, 王泽忠．三维静电场边界元法的积分精度问题[J]．高电压技术，2005，31(9)：21-24．

[11] 刘建军, 王建民. 边界元法在超高压变压器电场计算中的应用分析[J].变压器, 2008, 45(6):1-4.

[12] 汪沨, 范竞敏, 李敏, 等. 高精度上流有限元法在特高压直流输电线路离子流场计算中的应用[J]. 高电压技术, 2016, 42(4):1061-1067.

[13] 刘士利. 改进边界元法及其在电场计算中的应用[D]. 北京：华北电力大学, 2011.

[14] 季洁, 满家巨. 任意边界下的极小曲面造型问题[J]. 计算机与现代化,2007,(4):4-6.

[15] 王仁宏，李崇君，朱春钢. 计算几何教程[M]. 北京：科学出版社，2008.

[16] 盛剑霓. 工程电磁场数值分析[M].陕西：西安交通大学出版社，1991.

[17] 倪光正, 杨仕友, 邱 捷. 工程电磁场数值计算[M]. 北京：机械工业出版社, 2010.

[18] 李庆峰, 邓桃, 毛艳, 等. 1 000 kV特高压交流复合绝缘子耐张串均压特性研究[J]. 电网技术, 2013, 37(9):2541-2546.

Calculation of UHV Insulators String Electric Fields Based on Bezier Surface Quadrilateral BEM

LI Yasha, HUA Xu, SHEN Xingru, DAI Yaping

(College of Electrical Engineering and New Energy, China Three Gorges University, Yichang 443002, China)

In the boundary element calculation of three-dimensional electrostatic field, in order to calculate the intensity distribution of electric potential and electric field quickly and accurately, Bezier surface quadrilateral boundary element method (BEM) which uses the double quadric Bezier surface quadrilateral to fit the actual integral surface is proposed in this paper. This method uses second-order segmentation element’s node coordinates to construct double quadric Bezier surface parameter equation and uses Bezier surface parameter equation and area ratio method to construct shape functions corresponding to Bezier surface’s four vertex nodes. The number of node can be obviously decreased if the four vertex nodes are used as the computational node. Double quadric Bezier surface quadrilateral will fit the actual integral surface better when compared with the first-order plane quadrilateral BEM. So, Bezier surface quadrilateral BEM can improve calculation accuracy. And the function value of the model surface can be accurately displayed by the fine post-processing technique. The calculating results show that Bezier surface quadrilateral BEM has more accurate calculation results than the traditional BEM if they have the same grid segmentation nodes. Under the condition of same calculation accuracy, the Bezier surface quadrilateral BEM obviously requires fewer nodes, which needs less computer memory. Finally, the Bezier surface quadrilateral BEM are applied to the calculation of AC UHV insulator string electric field.

electrostatic field calculation; Bernstein primary function; Bezier surface; boundary element method；fine post-processing

10.3969/j.ISSN.1007-2691.2017.03.06

2016-08-26.

国家自然科学基金资助项目(51577105).

TM151

A

1007-2691(2017)03-0039-06

李亚莎(1967-)，男，副教授，研究方向为高压绝缘与电磁场数值计算；花旭(1993-)，男，硕士研究生，研究方向为高电压与绝缘技术。