考虑经济环境影响的有机朗肯循环区间不确定性多目标优化
王华荣,徐进良
(华北电力大学 低品位能源多相流与传热北京市重点实验室,北京 102206)
考虑经济环境影响的有机朗肯循环区间不确定性多目标优化
王华荣,徐进良
(华北电力大学 低品位能源多相流与传热北京市重点实验室,北京 102206)
针对热源温度和质量流量的参数波动特性,建立了有机朗肯循环的多目标优化模型,优化模型综合考虑了循环的热力性能、经济性能和环境性能的影响。目标函数是最大化系统输出净功和火用效率,最小化投资回收期和全生命周期的环境影响负载。循环的蒸发温度和冷凝温度为决策变量。引入了区间不确定性优化方法对热源参数波动的多目标优化模型进行求解,受热源参数区间变化的影响,区间不确定性优化参数对应的目标函数均为区间量,当热源参数变化幅度较大时,ORC系统的最优蒸发温度受热源参数变化幅度的影响较大,R141b的综合性能较优。使用区间不确定性多目标优化方法,可以简化优化过程,不需要再对热源变化引起的系统性能变化进行敏感性分析。
多目标优化;有机朗肯循环;区间不确定方法;经济性;环境影响
0 引 言
有机朗肯循环是利用有机工质蒸发温度较低的优势直接对低温热源回收发电的技术,是现在低温发电的研究焦点。在ORC系统的推广使用中,系统参数的优化成了设计过程中必不可少的重要环节。
目前,对系统参数优化的研究较多集中在单目标函数优化上。Quolin等[1]对废热回收应用的小规模ORC进行了技术经济优化,结果表明,对于相同的工质,采用不同的目标函数进行优化,会导致不同的最优参数。Khennich等[2]对亚临界和跨临界循环进行的建模分析,使用两个决策变量(循环最大压力和夹点温差)对4个目标函数(热效率、火用损、换热的热导、透平尺寸)分别进行优化分析。结果表明,最大化热效率和最小化火用损失的优化结果一致的,但与最小化热导和透平尺寸的优化结果是不一致的。Cayer等[3]选用了6个性能指标作为目标函数,对跨临界循环进行了优化研究,研究结果表明,对于不同的目标函数会得到不同的最优参数。Astolfi等[4,5]对低温地热分别进行了热力学优化研究和技术经济优化研究,确定了不同研究目标下的系统最优工质、循环结构和循环参数,两部分优化结果进行比较的结果表明,研究目标不同,最优参数存在一定差异。
上述多个研究结果表明,不同的目标函数会导致不同的最优参数。也就是说,单目标优化不能解决多个目标函数冲突的问题,因此,多目标优化的方法逐渐引起了越来越多学者的注意。Wang等[6]选取单位净功所需的换热面积和热回收效率为目标函数,以及蒸发压力、冷凝压力、工质的流速和冷凝水的流速为决策变量,对ORC系统进行多目标优化,得到不同热源温度条件下的最优工质及最优参数。Pelet等[7]在偏远社区的集成能源供应系统的设计、规划和管理过程中同时考虑了经济性和环境因素,以总成本和CO2排放量为评价目标进行了优化。Papadopoulos等[8]考察了包括经济、运行、安全和环境在内的系统综合性能。Wang等[9]以火用效率和总投资成本作为优化指标,得到系统在热力学和经济性方面的最优运行参数。Pierobon等[10]将热效率、系统总体积和净现值作为目标函数,得到最优的系统参数。由此可见,对ORC系统参数的多目标优化较多集中在热力性和经济性上,很少有考虑系统的环境影响,特别是没有考虑系统的全生命周期环境影响。
综合分析发现,无论是单目标优化,还是多目标优化,优化都是在热源参数为恒定值的条件下进行的。然而,有机朗肯循环的应用范围较为广泛,包括太阳能、生物质能、沼气、地热能、工业余热等方面,这些热源大都具有波动性和间歇性。在系统设计和实际应用中,往往是将波动的热源假定为稳定热源,或者是在热源端增加导热油循环将其转换为稳定热源,这样不仅导致设计的系统对变化热源的适应性较差,而且增加了系统的复杂度和成本。
因此,针对热源的波动特性,本文建立了一个多目标优化模型,综合考虑ORC系统的热力性、经济性和全生命周期环境性,引入区间不确定性优化方法,在优化过程中综合考虑热源波动性的影响,不需要得到系统最优参数之后再对热源变化引起的系统性能变化进行敏感性分析,简化了优化过程。
1 热力学分析
选用基本的ORC循环,设备主要包括蒸发器、透平、冷凝器、工质泵,系统原理如图1所示。ORC系统热力循环过程T-s图如图2所示,有机工质经过蒸发器吸收废热热源的热量,产生高温高压蒸汽(5-1);高温高压蒸汽进入透平膨胀做功带动发电机发电(1-2);透平排气经过冷凝器凝结为饱和液体,对外放热(2-4);饱和液体经工质泵进行加压(4-5)。为了简化理论分析,系统选用干工质,并对系统作如下假设:循环在热源波动后很快恢复稳态流动;冷凝器出口工质为饱和液体;蒸发器出口工质为饱和气体;设备和环境间的散热忽略不计;蒸发器、冷凝器和连接管道的压力损失忽略不计。
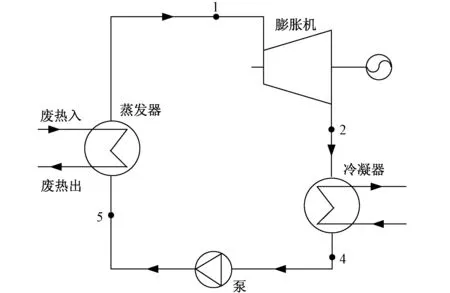
图1 基本ORC结构图Fig.1 The basic ORC configuration
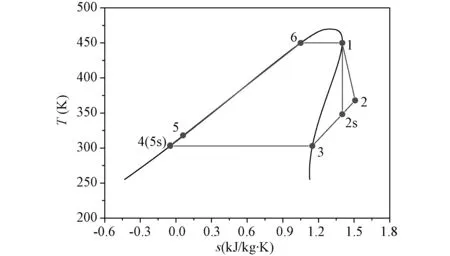
图2 ORC的T-s图Fig.2 The T-s diagram of ORC
对ORC系统的热力过程进行分析,如下:
膨胀过程1-2:理想状态下,膨胀过程为可逆绝热过程1-2s。工质所做的功为
(1)
不可逆损失为
(2)
冷却过程2-4:工质放出的热量可由下式计算:
(3)
不可逆损失为
(4)
加压过程4-5:理想状态下,加压过程是绝热过程4-5s。由于工质泵加压后,工质温升很小,状态点4和5s基本重合。泵的做功量为
(5)
泵的不可逆损失为
(6)
吸热过程5-1:工质吸收的热量可由下式计算
(7)
吸热过程产生的不可逆损失为
(8)
输出净功为
(9)
总的火用损失为
(10)
系统的总火用可以表示为
(11)
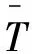
(12)
因此,循环的火用效率为
(13)
2 经济性模型
系统主要设备的成本采用化工常用的模块成本核算方法来计算(CEPCI2012=584.6)[11]。若考虑所有的直接和间接成本,则设备成本(baremodulecost)为
(14)
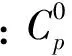
(15)
式中:A是容量或部件的尺寸参数,K1、K2和K3是每个部件特有的常量参数。
对于其他部件,FBM是直接给出的。对于换热器和泵来说,FBM的表达式为
FBM=B1+B2FpFM
(16)
其中,B1和B2取决于换热器类型(双管、管壳或空冷),泵(循环泵或离心泵)。
FM为材料因子;Fp为压力因子,可由下式计算得到
(17)
式中:p为压力;C1、C2和C3是不同部件的系数。
本文ORC系统的设备成本计算中,式(14)~(17)中的常数取自文献[11]。
不同工质和系统参数导致系统设备的参数不同,由于各系统的投资额不等,因此,采用经济学上的投资回收期(PBP)来评价投资方案的优越,计算公式如下:
PBP=-ln(1-kC0/Fn)/ln(1+k)
(18)
式中:Fn为第n年的净现金流;Fn=Bn-Cn,Bn为第n年的收益(输入流);Cn为第n年的成本(输出流),这里假设为常数;C0为初期投资成本;k为利率。
在ORC系统的成本计算中,为了简化计算,建设成本仅考虑主要设备的成本,包括膨胀机、蒸发器、冷凝器和工质泵,忽略其他组件成本。假设后期运行过程中维护成本占总成本的2%,耗材占总成本的0.3%,管理和安全措施的费用占总成本的0.7%,系统运行周期为20年,有效运转率为85%,系统折旧率为2%,利息率为5%,工业用电电价取1¥/kW·h,约0.1622 S|(按照2014年8月26日汇率换算)。
3 环境性模型
采用LCA(Life Cycle Assessment)对环境性进行评价,遵循ISO14040标准。基于中国科学院生态环境研究中心建立的全生命周期评价(LCA)的模型框架对ORC系统进行环境影响分析。
以1 kW·h为功能单位,将ORC系统的整个生命周期作为研究对象。由于缺乏建设ORC系统的详细数据,本文只考虑系统的主要部件(蒸发器、冷凝器、膨胀机和工质泵),忽略其他部件(如管道等),忽略建筑及土木工程方面的因素。因此,系统涉及到的主要原材料是不锈钢,ORC系统边界如图3所示,包括主要原料的开采、生产和使用,以及系统的建设、运行和退役过程。
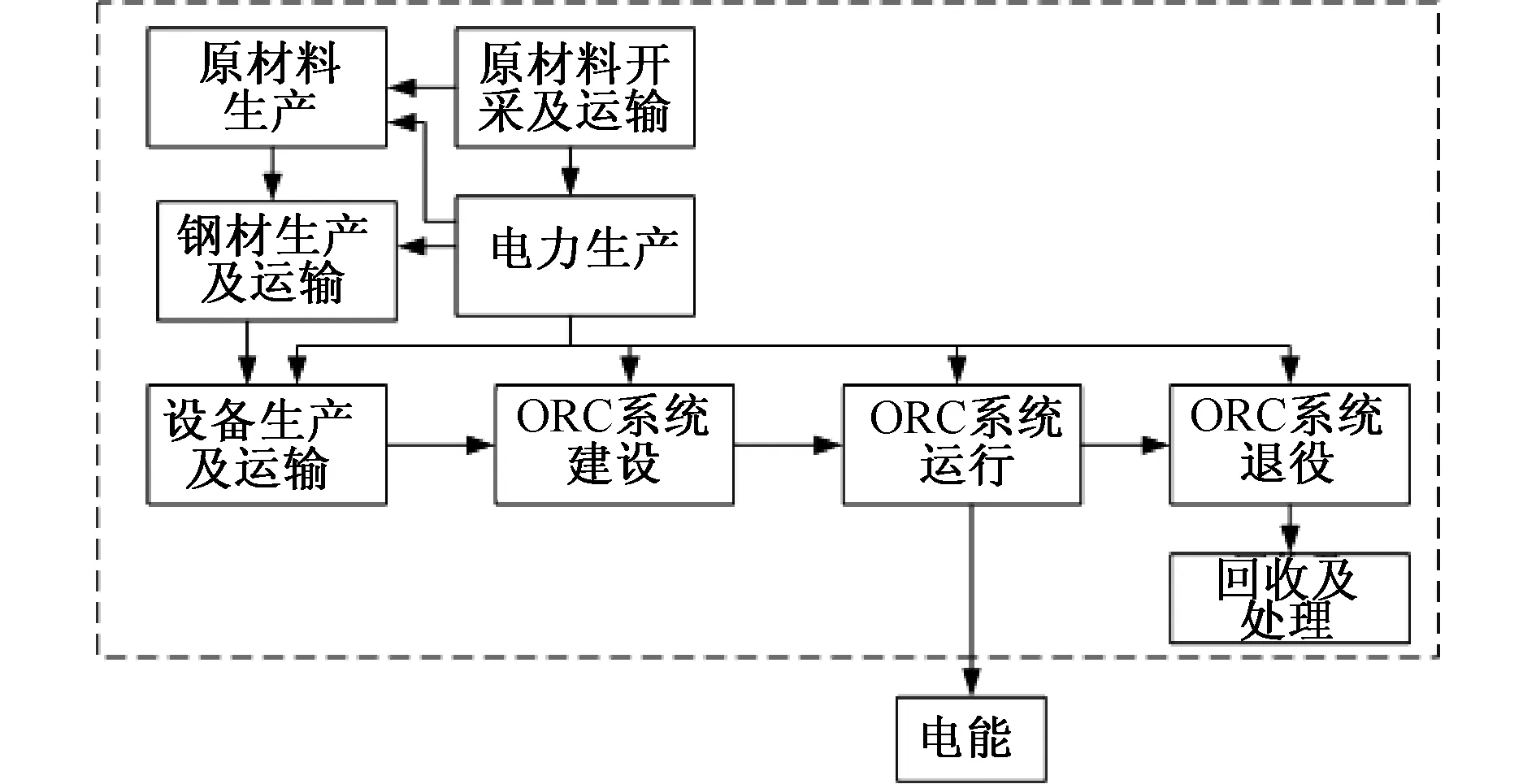
图3 ORC的边界图Fig.3 The boundary of ORC
本文使用中国科学院生态环境研究中心开发的中国能源数据库以及主要原材料的数据库。ORC系统是利用工业废热,因此,在运行阶段不会引入新的排放;系统的主要材料为不锈钢,系统退役后,不锈钢可回收再利用,只涉及到废弃不锈钢设备的运输问题。ORC系统的排放数据主要包括系统建设阶段涉及到的原材料的开采、生产和运输等排放数据;系统退役阶段的运输废弃物的排放数据。整个过程的运输均采用公路货运的方式,距离采用2012年国家统计数据公路货物运输平均运距186.72 km[12]。
根据模型框架,选取GWP(温室效应潜能)、AP(酸化潜能)、EP(富营养化潜能)、HTP(人体毒性潜能)、SWP(固体废物潜能)和SAP(烟尘和粉尘潜能)作为评价的影响类型。影响评价模型包括一下几个计算步骤[13,14]:
(1)影响潜值的计算:
(19)
式中:EP(j)为系统对第j种潜在环境影响的贡献;EP(j)i为第i种排放物质对第j种潜在环境影响的贡献;Qi为第i种物质的排放量;EF(j)i为第i种排放物质对第j种潜在环境影响的当量因子,当量因子取自文献[15]。
(2)影响潜值的加权值计算:
(20)
式中:ER(j)T2000为2000年全球或地区环境影响潜值总和。
(3)环境影响负荷(Environmental Impact Load, EIL)的计算:
EIL=∑WP(j)
(21)
4 多目标优化
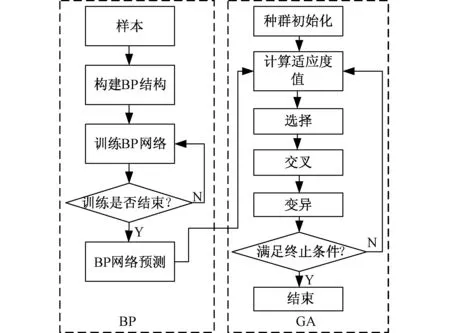
不确定系统参数的优化方法是一种针对不确定环境下的参数优化方法,它更适合于对存在参数变化的系统进行优化。一般情况下,热源的温度和质量流量的变化范围更容易确定,属于区间变化,可以采用区间不确定性优化方法对系统参数进行优化。
4.1 不确定性多目标优化模型
根据前面的分析,选取蒸发温度和冷凝温度作为决策变量;选取循环的输出净功、火用效率、投资回收期、环境影响负荷作为目标函数,要求最大化循环输出净功和火用效率,最小化投资回收期和环境影响负荷。
在优化过程中考虑热源参数(温度和质量流量)变化,优化问题可描述为
(22)
约束条件为:
(1)为保证传热能够进行,蒸发温度应小于热源入口温度,且蒸发端夹点温差大于最小传热温差值(5K),即
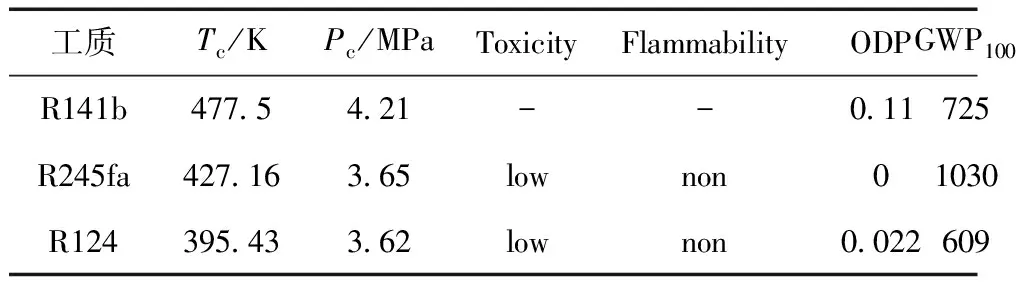
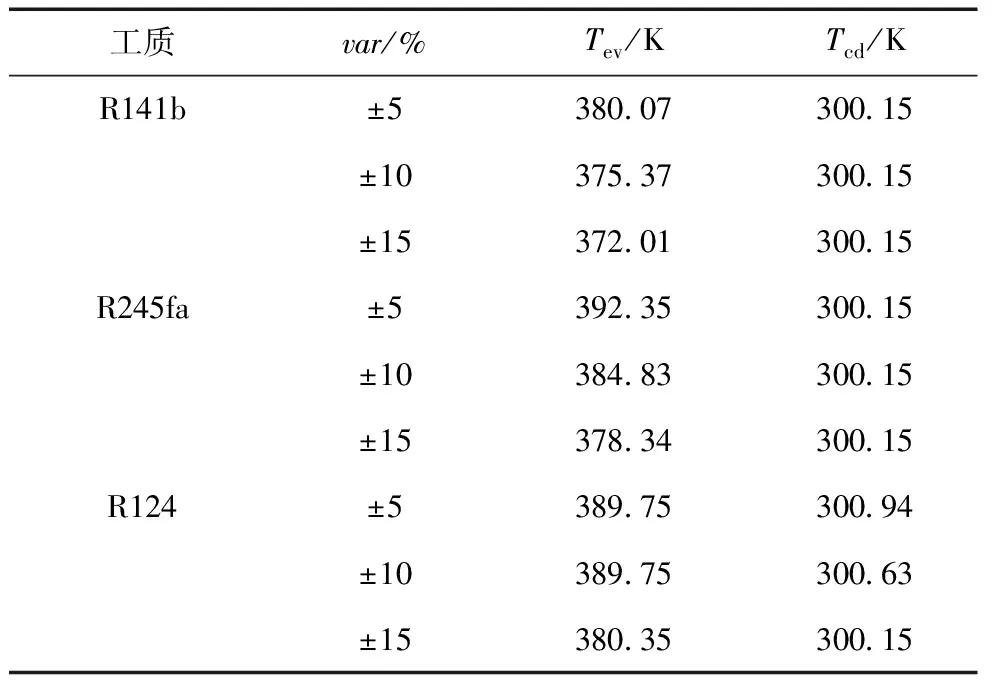
(2)蒸发温度应高于冷凝温度,冷凝温度应高于环境温度。
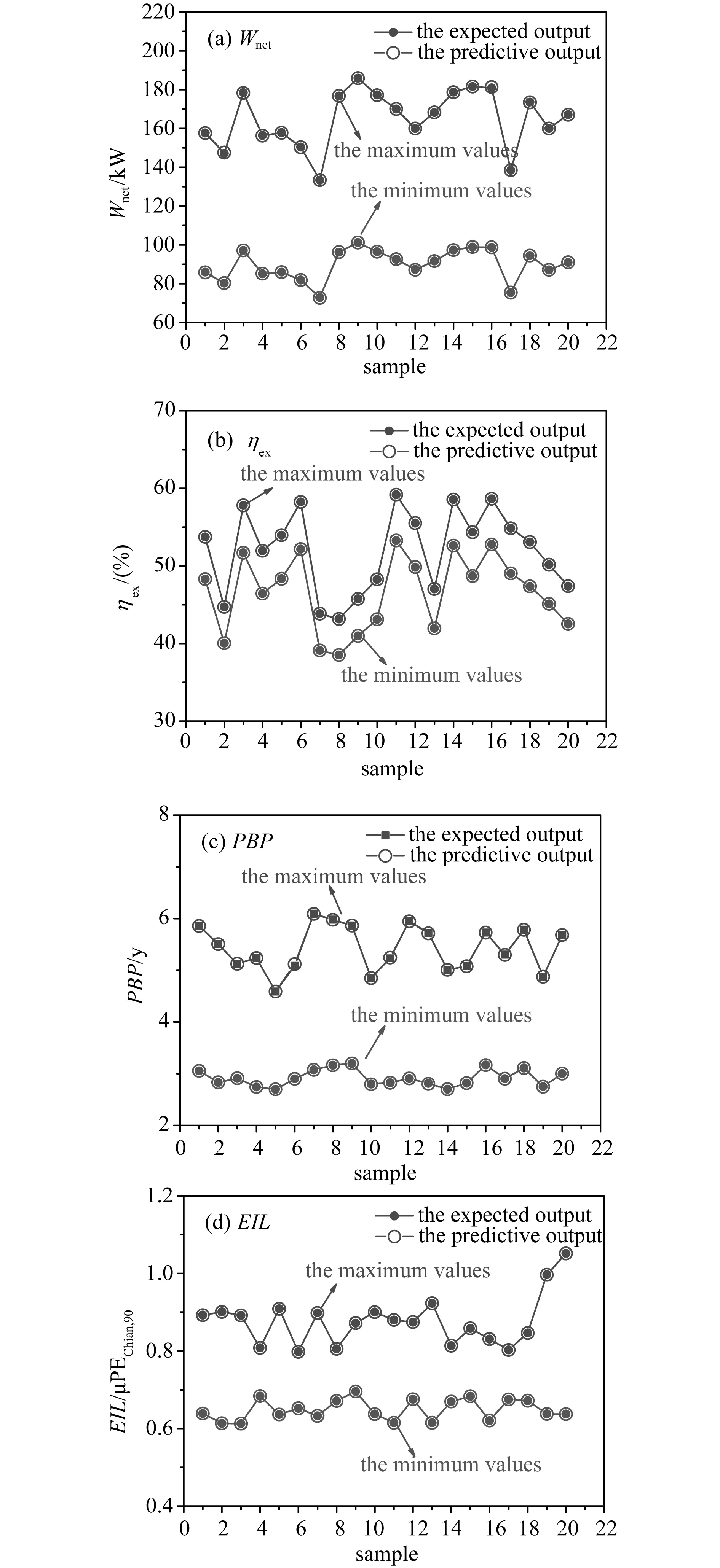
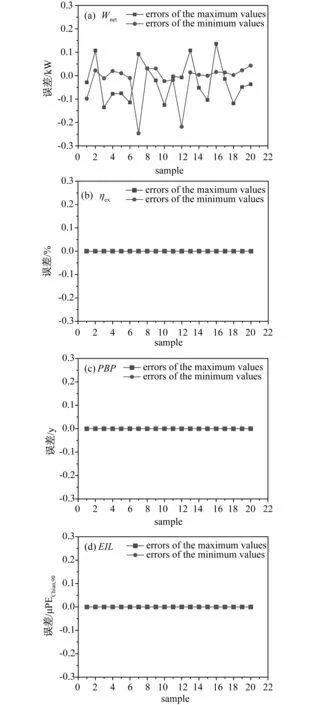
(3)对于亚临界ORC系统,蒸发温度对应的压力Pev(Tev)应小于工质的临界压力Pc,同时,为了避免工质在膨胀过程中进入两相区,设定Pev(Tev)小于T-s图中气相段上的最大s值对应的压力P(smax)。因为P(smax) (4)热源温度和流量的区间范围: 4.2 区间不确定性多目标优化算法 为了描述方便,将式(22)表述的模型改写成 (23) 由于区间参数的影响,目标函数fi′的值也是一区间量,可表示为 (24) 根据区间的序关系“≤mw”,可以通过目标函数的中点值和宽度来判断不同决策变量的优劣,因此,对于每个目标函数,优化问题可以转化为 (25) 引入权系数β∈[0,1],优化问题可以转化为 (26) 由此可见,在对目标函数进行优化的过程中,存在着两层优化,首先对目标函数进行优化,求解每一个决策变量对应的目标函数的取值区间,然后,在对所求解的目标函数取值区间的中点值和宽度值进行优化。为了简化计算,本文将神经网络和遗传算法结合起来[16](流程图如图4所示),利用神经网络的网络模型,得到决策变量和目标函数最大、最小值之间的映射关系,将优化求解过程简化为一层优化问题。具体求解过程为:第一,利用遗传算法对一组随机决策变量进行优化,得到目标函数的取值区间;第二,将决策变量和对应的目标函数的取值区间构成一组样本数据,对构建的神经网络结构进行训练,得到它们之间的映射关系;第三,对每一个决策变量,利用训练好的网络结构直接映射得到对应目标函数的取值区间;第四,利用遗传算法对目标函数的取值区间的中点及宽度值进行优化。 图4 BP-GA流程图Fig.4 Flow char of BP-GA 选取余热热源参数变化区间的中值为:温度180 ℃,质量流量11kg/s。余热经过ORC系统的出口温度设定为90℃,系统膨胀机的等熵效率为85%,工质泵的等熵效率为80%,采用环境温度(20 ℃)下的水为冷却介质,冷凝温度的取值区间设定为[27, 40]℃,冷凝端的夹点温差设定为5K。余热热源温度和质量流量的波动范围分别取var=±5%, ±10%, ±15%的变化量,则热源温度的取值区间依次为:[171, 189] ℃,[162, 198] ℃,[153, 207] ℃;热源质量流量的取值区间依次为:[10.45, 11.55] kg/s,[9.90, 12.10] kg/s,[9.35, 12.65] kg/s。以NIST的REFPROP9.0为工质库,根据课题组的研究成果,工质的临界温度筛选准则,综合考虑工质各方面的特性,选取R141b, R245fa和R124 三种有机工质作为ORC循环的运行工质。工质的参数详见表1。 表1 三种工质的主要参数 在区间不确定性优化过程中,利用人工神经网络模型,得到决策变量和目标函数最大、最小值之间的映射关系。对每个目标函数分别建立BP神经网络模型,BP神经网络结构为2-10-2,即输入层有2个节点,隐含层有10个节点,输出层有2个节点。输入参数是蒸发温度和冷凝温度,输出参数是各目标函数的最大、最小值。节点的传递函数为tansig函数,训练函数为trainlm。对蒸发温度和冷凝温度随机采样100组数据,通过热力学计算得到输入、输出数据,随机选取80组输入输出数据作为训练数据,用于网络训练,20组数据作为测试数据,用于测试网络的拟合性能。以工质R245fa和热源参数var=±10%的变化区间为例,用训练好的神经网络预测函数输出,预测结果如图5所示,网络预测相对误差如图6所示。相对误差百分比定义为期望输出值与预测输出值的绝对差值除以期望输出值的百分数,则4个神经网络的误差百分比均小于0.05%,说明经过训练的网络有较好的预测性能。基于建立好的4个神经网络模型,对于给定的蒸发温度和冷凝温度作为输入参数,都可以预测出所对应目标函数的最大、最小值。 图5 BP神经网络的预测Fig.5 BP neural network prediction 图6 BP神经网络的预测误差Fig.6 The prediction errors of BP neural network 在区间不确定性优化的求解中,引入了系数β,即每个目标函数值区间的中心点和宽度值在优化中所占的比重。本文在优化过程中,主要考虑ORC系统性能的稳定性,即偏重考虑区间宽度值,令β=0.4。三种不同工质ORC系统的区间不确定性优化的最优解见表2。可见,工质R141b和R245fa的最优蒸发温度受热源参数变化幅度大小的影响较大,但最优冷凝温度不受影响,保持在最低冷凝温度值;工质R124,热源参数变化幅度较小时,最优参数变化较小,但热源参数变化幅度较大时,最优参数变化较大。最优解对应的各目标函数的取值区间见表3,可见,各目标函数受热源参数波动的影响,均为区间量,同时,随着参数变化区间的大小不同,它们的取值区间也不同,随着参数变化幅度的增加,它们取值区间的宽度也随之增加,区间的中心值随着最优解的不同而不同,具体变化趋势如图7所示。比较三个不同工质循环的综合性能,R124的综合性能最差,而R141b和R245fa的综合性能较为接近,当参数的取值区间变化量var=±5%时,R245fa的综合性能较优,而当var=±10%, ±15%时,R141b的综合性能较优。 表2 区间不确定性优化最优解 Tab.2 The optimal solutions of the interval uncertainty optimization 工质var/%Tev/KTcd/KR141b±53800730015±103753730015±153720130015R245fa±53923530015±103848330015±153783430015R124±53897530094±103897530063±153803530015 表3 区间不确定性最优解对应的目标值范围 Tab.3 The range of the objective function values using the interval uncertainty optimization 工质var/%Wnet/kWηex/%PBP/yEIL/μPEChina,90R141b±5[12866,17394][5334,5625][239,319][070,082]±10[10411,19125][5005,5568][213,371][067,087]±15[8353,21040][4743,5571][194,446][065,093]R245fa±5[1287417408][5405,5696][308,422][067,079]±10[10371,19041][5042,5603][267,485][064,085]±15[8203,20648][4710,5524][240,579][063,091]R124±5[11490,15538][5020,5283][441,594][067,074]±10[9705,17822][4911,5438][391,718][064,080]±15[7801,19651][4627,5403][339,849][065,088] 图7 最优参数对应目标函数取值区间的中值和宽度值Fig.7 The middle and width of the objective function values corresponding to the optimal solutions of the interval uncertainty optimization method 本文通过对ORC系统的热力性、经济性和环境性进行分析,提出了以循环输出净功、火用效率、投资回收期和环境影响负荷为目标函数,以蒸发温度和冷凝温度为决策变量的不确定性参数的多目标优化模型。在热源温度和质量流量为区间变化的情况下,采用区间不确定性优化方法对多目标模型进行了求解。主要得出以下结论: (1)采用参数区间变化的不确定性多目标优化的结果表明,热源参数变化幅度较大时,ORC系统的最优蒸发温度受热源参数变化幅度的影响较大。 (2)受热源参数区间变化的影响,区间不确定性优化参数对应的目标函数均为区间量。比较三个不同工质循环的综合性能,R124的综合性能最差,而R141b和R245fa的综合性能较为接近,当参数的取值区间变化量var=±5%时,R245fa的综合性能较优,而当var=±10%, ±15%时,R141b的综合性能较优。 (3)将热源参数不确定性变化引入循环优化设计中,不再需要对热源参数的变化进行系统敏感性分析,简化了优化设计过程。 [1] QUOILIN S, DECLAYE S, TCHANCHE B F, et al. Thermo-economic optimization of waste heat recovery Organic Rankine Cycles [J]. Applied Thermal Engineering, 2011, 31(14): 2885-2893. [2] KHENNICH M, GALANIS N. Optimal design of ORC systems with a low-temperature heat source [J]. Entropy, 2012, 14(2): 370-389. [3] CAYER E, GALANIS N, NESREDDINE H. Parametric study and optimization of a transcritical power cycle using a low temperature source [J]. Applied Energy, 2010, 87(4): 1349-1357. [4] ASTOLFI M, ROMANO M C, BOMBARDA P, et al. Binary ORC (organic Rankine cycles) power plants for the exploitation of medium-low temperature geothermal sources-Part A: Thermodynamic optimization [J]. Energy, 2014, 66: 423-434. [5] ASTOLFI M, ROMANO M C, BOMBARDA P, et al. Binary ORC (Organic Rankine Cycles) power plants for the exploitation of medium-low temperature geothermal sources-Part B: Techno-economic optimization [J]. Energy, 2014, 66: 435-446. [6] WANG Z Q, ZHOU N J, GUO J, et al. Fluid selection and parametric optimization of organic Rankine cycle using low temperature waste heat [J]. Energy, 2012, 40: 107-115. [7] PELET X, FAVRAT D, LEYLAND G. Multiobjective optimisation of integrated energy systems for remote communities considering economics and CO2 emissions [J]. International Journal of Thermal Sciences, 2005, 44(12): 1180-1189. [8] PAPADOPOULOS A I, STIJEPOVIC M, LINKE P. On the systematic design and selection of optimal working fluids for Organic Rankine Cycles [J]. Applied Thermal Engineering, 2010, 30(6): 760-769. [9] WANG J, YAN Z, WANG M, et al. Multi-objective optimization of an organic Rankine cycle (ORC) for low grade waste heat recovery using evolutionary algorithm [J]. Energy Conversion and Management, 2013, 71: 146-158. [10] PIEROBON L, NGUYEN T V, LARSEN U, et al. Multi-objective optimization of organic Rankine cycles for waste heat recovery: Application in an offshore platform [J]. Energy, 2013, 58: 538-549. [11] TOFFOLO A, LAZARETTO A, MANENTE G, et al. A multi-criteria approach for the optimal selection of working fluid and design parameters in Organic Rankine Cycle systems [J]. Applied Energy, 2014, 121(5): 219-232. [12] 中国国家统计局.国家统计年鉴2013[M].北京:中国统计出版社,2013. [13] 杨建新.产品生命周期评价方法及应用[M].气象出版社,2002. [14] 王华荣,徐进良,于超. 有机朗肯循环在水泥工业余热利用中的环境经济性分析[J]. 华北电力大学学报(自然科学版),2015,42(3):64-70. [15] LIU C, HE C, GAO H, et al. The environmental impact of organic Rankine cycle for waste heat recovery through life-cycle assessment [J]. Energy, 2013, 56: 144-154. [16] 王小平,曹立明. 遗传算法-理论、应用与软件实现[M]. 西安:西安交通大学出版社,2001. Multi-objective Optimization of Organic Rankine Cycles Based on Interval Uncertain Method Considering Environmental and Economic Performance WANG Huarong, XU Jinliang (Beijing Key Laboratory of Multiphase Flow and Heat Transfer, North China Electric Power University, Beijing 102206, China) We present the multi-objective parameter optimization of organic Rankine cycles (ORCs) according to the fluctuation parameters of heat sources and mass flow rates such as varied temperatures and flow rates of the heat carrier fluid. The thermal, economic and environmental impacts of sub-models are considered in the optimization model. The objective functions are the environmental impact load which can maximize the net output power and energy efficiency and minimize the pay-back-period (PBP) and (EIL). The evaporation and condensation temperatures are the control variables. In this paper, the uncertain optimization method is applied to deal with the optimization problem for heat sources with varied parameters. Affected by the heat source parameters, the objective functions are interval. When the variation of the heat source parameters is large, the variation of the optimal evaporation of the ORC system is large. The comprehensive performance of R141b is best. The interval uncertainty method can simplify the ORC optimization process. And the sensitivity analysis of system performance variation aroused by heat source variation is no longer needed. multi-objective optimization; organic Rankine cycle; interval uncertain method; economic performance; environment impact 10.3969/j.ISSN.1007-2691.2017.03.12 2016-09-18 国家自然科学基金国际合作项目(51210011). TK 123 A 1007-2691(2017)03-0081-09 王华荣(1981-),女,博士研究生,主要从事低品位能源清洁利用的研究工作。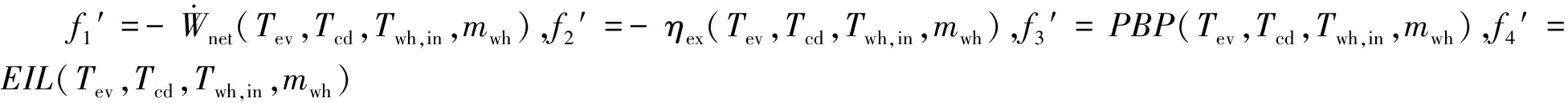
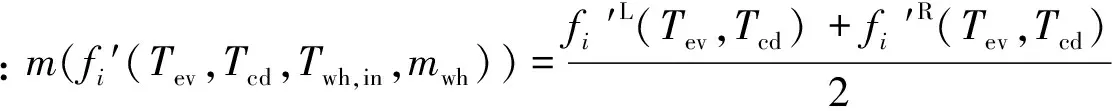
5 结果与讨论

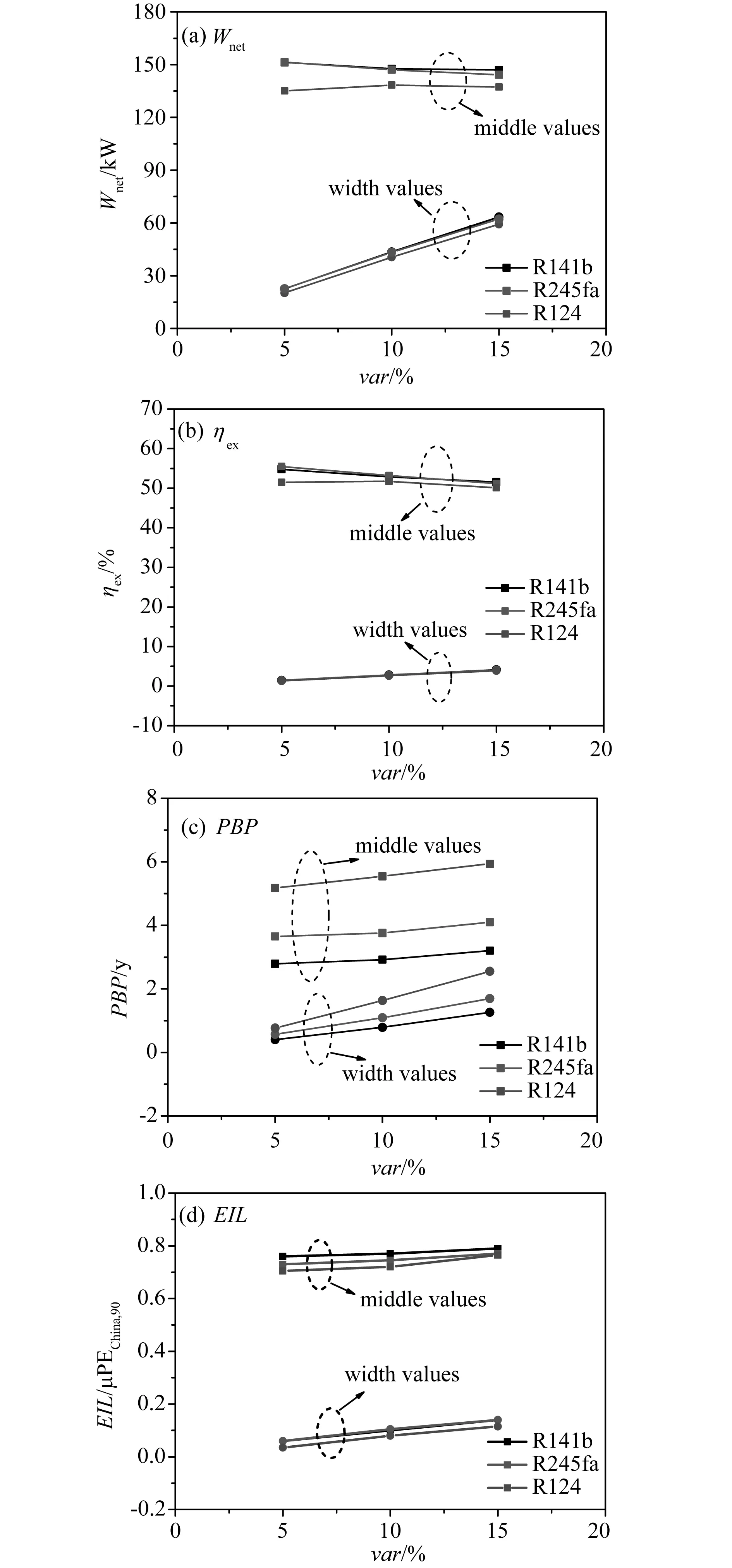
6 结 论

