基于最大相关峭度解卷积算法的发电机特征振动信号增强检测

何玉灵，王 珂，仲 昊，蒙玉超，王晓龙，唐贵基

(1.华北电力大学 能源动力与机械工程学院，河北 保定 071003；2.北京理工大学 机电学院，北京 100081)



基于最大相关峭度解卷积算法的发电机特征振动信号增强检测

何玉灵1，王 珂2，仲 昊1，蒙玉超1，王晓龙1，唐贵基1

(1.华北电力大学 能源动力与机械工程学院，河北 保定 071003；2.北京理工大学 机电学院，北京 100081)

采用最大相关峭度解卷积算法(MCKD)对发电机定子的振动信号进行处理，得到信号处理后的时域波形与频谱，并根据提取得到的故障特征信息实现了对发电机运行状态的识别。为了排除偶然性，用最大相关峭度解卷积算法对发电机定子的正常信号和定子匝间短路故障信号都进行了处理，从而证明了这一算法用于振动信号故障特征提取的有效性。通过和当前主流算法之一的最小熵解卷积算法(MED)的处理结果进行对比，分析发现本文算法比最小熵解卷积算法的故障特征信息提取更加明显和准确。结果表明，最大相关峭度解卷积对故障信号特征频率的提取有良好的效果，并与当前主流算法相比有一定的优越性。

发电机；定子匝间短路；振动信号；最小熵解卷积(MED)；最大相关峭度解卷积(MCKD)

0 引 言

振动是对发电机影响较大的故障之一，本文便是研究发电机振动故障的分析。在振动的各个原因中，定转子的故障占据了很大部分。发电机振动对其正常运行有很大的影响，轻微振动可以继续使用，但容易发热、磨损等，严重些的故障会对发电机造成严重危害，必须停机检查修理[1，2]。因而发电机振动信号的分析至关重要。

过去的不少研究者对信号处理方法进行了多次研究，滤噪处理技术逐步成熟[3-6]，模式识别技术不断发展[7-9]，滚动轴承故障信号的提取技术也取得了不少成绩[10-14]，但是发电机振动信号分析更为复杂。同时，从文献[15]和[16]可知，发电机定子匝间短路下定子的特征振动频率为2f、4f、6f，但是原始振动信号的特征频率幅值甚至要低于噪声等其他非特征信号。因而对发电机振动信号进行进一步的处理分析至关重要。

本文将在当前主流算法之一的最小熵解卷积算法基础上，提出最大相关峭度解卷积算法，并将其应用于发电机定子匝间短路故障信号的特征提取中。

1 最小熵解卷积算法

本文所涉及的最小熵解卷积算法(MED)为当前信号处理流行的一种主流算法，广泛用于滚动轴承、齿轮等旋转机械部件故障振动信号处理中。在信息化领域，熵可以对信息进行定量的描述。对于本文研究的发电机定子振动信号来说，拥有特定的频率特征即为有不均匀的概率分布，因而要取其最小熵值来对输入信号进行度量。文献[17]对这一算法进行了研究：

采集到的振动信号x可用时域卷积表示为

(1)

式中：x=[x1,x2,x3,… ,xN]T，是离散的加速度信号；u=[u1,u2,… ,uN]T，为未知的输入干扰信号；d=[d1,d2,… ,dN]T，是输入周期性的冲击故障信号；e是离散的高斯噪声序列；hu，hd，he为对应的滤波器的系数；N是加速度序列数据x的长度。

用滤波器得到的输入信号y可用时域卷积表述成如下公式：

(2)

该式子可表述为

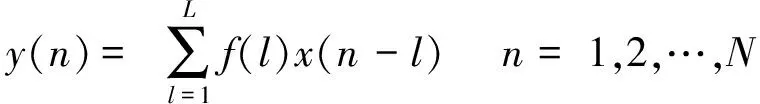
(3)

式中：f=[f1,f2,… ,fL]T，y=[y1,y2,… ,yN]T。

利用目标函数法，将最小熵解卷积法转化为峭度。同样的，当数据分散程度大，即特征频率处的幅值没有明显突出时，峭度值小。对y求关于f的峭度最优值，即

(4)

式中：μy=0；L、N分别是滤波器f的长度与信号x的长度。

对峭度K(y)求关于f的一阶偏导，为求取K(y)的最大值，应将其偏导数等于零，通过化简将其整理为以下矩阵形式：

(5)

其中：

2 最大相关峭度解卷积算法

2.1 最大相关峭度解卷积算法原理

峭度能够表示出振动信号的分布特征，且对突出的冲击脉冲十分敏感。在峭度的基础上添加了解卷积周期参数T即为相关峭度，相关峭度能够减弱突出的脉冲，将冲击信号的影响降至最低[18]。解卷积又称反褶积，是一种能够消除之前所做的滤波处理的方法，能从滤波器得出的输出信号中得到原始的输入信号。最大相关峭度解卷积(MCKD)是一个新的信号处理方法，它不仅能消除信号传递路径的影响，还能抑制环境噪声的干扰，并能有效地提取原始故障信号。其处理结果与有效参数的选择相关，而本文通过局部优化滤波器长度L来使得信号的处理更加有效。

当一个局部缺陷出现在发电机定子中时，正常部分和故障部分的相互作用就会导致周期性的振动。从传感器中收集到的信号会表现为重复的影响序列。假设拥有局部缺陷的发电机定子的振动信号被描述成如下所示：

(6)

式中：x是在样本N中收集的振动信号；u是由局部缺陷导致的周期性影响信号；e是环境噪声；hu和he是FIR滤波器对于他们各自系统法传递函数近似值。

MCKD旨在通过把含有样本L的FIR滤波器应用到已获得的信号x中。

(7)

通过选择最佳的滤波器f将噪声影响减小到最低(f*(he*e)→0)，并提取周期性影响信号的近似值(f*(hu*u)≈u)可以实现这一目标。

一个命名为相关峭度的新的指标定义在MCKD算法中，来评估作为结果的信号y，这一指标能有效地测量信号中周期性影响的比例。

(8)

式中：N表示信号的长度；T是解卷积周期；M是转换的数目。

相关峭度指标的最大值被看作是在MCKD算法中用来寻找过滤系数最佳集合的最优化目标。相对于峭度对少数突出脉冲的反应太过敏感，相关峭度能够对连续的尖脉冲有所反应。而为了使连续的尖脉冲突出，需要取相关峭度的最大值。

(9)

过滤系数fk相当于最大相关峭度，能够通过求出CKM(T)分子分母的导数来获得。

(10)

然后，f的结果能够通过以下公式被推导出：

(11)

2.2 算法流程

本文算法的主要流程如图1所示，对应步骤如下：

(1)取T值。T为解卷积周期，实际为进行信号处理时将某个数据点和与此数据点间距T个数据点的数进行处理。本文所述发电机基频为50 Hz，因此冲击信号的时间间隔为0.02 s，而采样频率为5 000 Hz，相当于每秒采样5 000个数据点，因此间隔的0.02 s采样了100个数据点。则T取值为100。

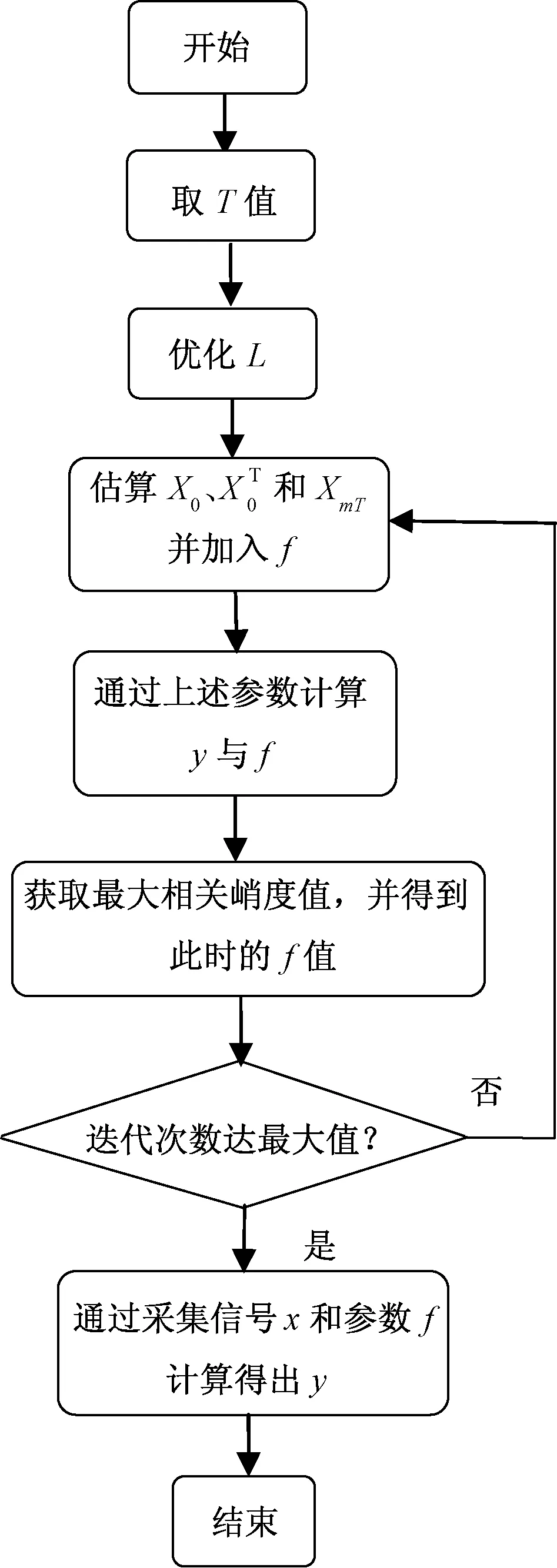
图1 算法流程图Fig.1 Flow chart of the algorithm

(2)优化滤波器长度L。对L取值2到190，逐一代入MCKD算法中，取相关峭度最优时L的取值，确定为最优的滤波器长度。

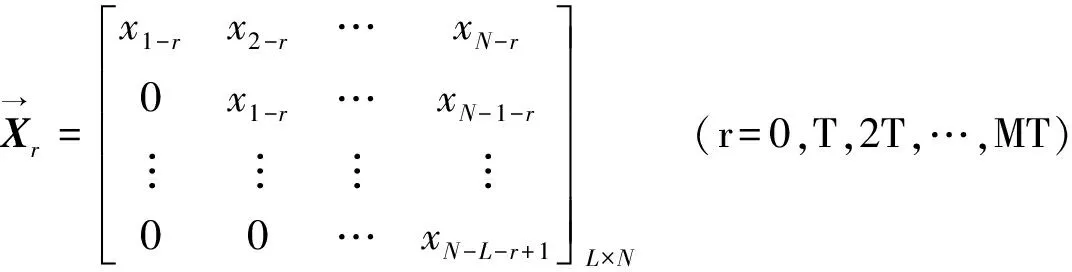
(3)通过已获得的信号x估算X0、X0T和XmT；

(4)在样本中加入滤波器系数f；

(5)由公式(7)计算y，并根据信号y计算αm和β；

(6)由之前的参数计算f；

(7)计算相关峭度值，与之前获得的最大相关峭度值对比，将较大值赋予最大相关峭度值，并获取此时的f；

(8)确定迭代次数是否达到规定的最大值。如果达到，那么进程将会停止，否则就返回到步骤(3)。

(9)由采集信号x和最大相关峭度下的滤波器系数f获取输入信号y。

3 定子特征信号检测

3.1 实验信号获取

为了获取短路故障研究所需的数据，在新能源电力系统国家重点实验室MJF-30-6型动模发电机组上进行模拟实验，如图2(a)所示。

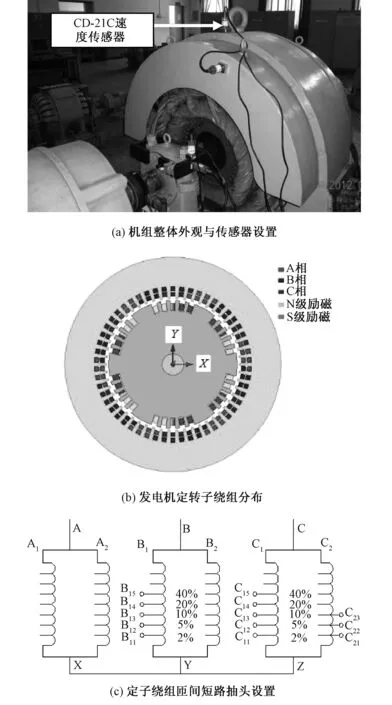
图2 实验设备与方法Fig.2 Experimental equipment and method

机组主要的参数如下：额定功率：24 kW，额定容量：30 kVA，额定电压：400 V，功率因数：0.8，额定转速：1 000 r/min，基频，50 Hz；极对数：p=3，绕组相数：3，定子槽数：Z1=54，每极每相槽数：q=3，定子绕组匝数：72，并联支路数：a=2，同步电抗：xs=2.030 8 Ω。

实验通过短接不同短路抽头来对不同程度的定子匝间短故障进行模拟。定转子绕组的分布及定子匝间短路抽头设置如图2(b)、(c)所示。

短路故障数据是通过CD-21C速度传感器获得的，其灵敏度为30 mV/mm/s，如图2(a)所示。本文先测取发电机正常运行条件下的定子振动数据作为比对，然后将C相第二条支路的C21和C22处短路，获取3%定子短路故障数据1，再将C相第一条支路Z和C12处短路，获取5%定子短路故障数据2。

3.2 定子振动信号分析

分别对定子的正常振动信号、3%定子匝间短路和5%定子匝间短路进行分析，原始信号、MED算法处理结果和本文算法MCKD处理结果分别如图3～图5所示。

从图3中可以看出，原始的故障信号十分杂乱，定子正常原始信号的规律性不能明显地表现出来，尤其在频域图中，整个谱图并无规律，发电机定子的振动特征与图中的幅值谱线不契合，在2f、4f、6f这些特征频率处并没有明显的幅值，与我们要提取的故障特征相差甚远。图4中MED算法处理后的信号与原始信号相比有了较大的改观，特征频率处的幅值有了较大的提升，表明了MED算法能够有效地提取到故障特征信息。

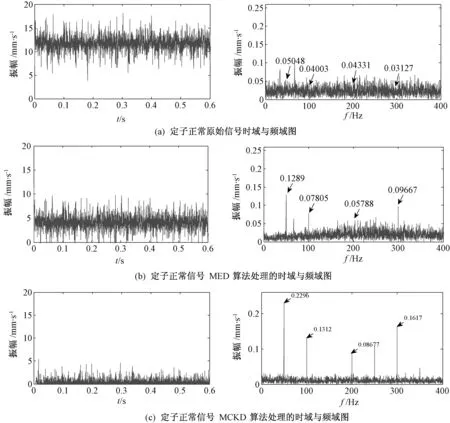
图3 定子正常信号时域波形及频谱Fig.3 Stator vibration signal in normal condition with different processing methods

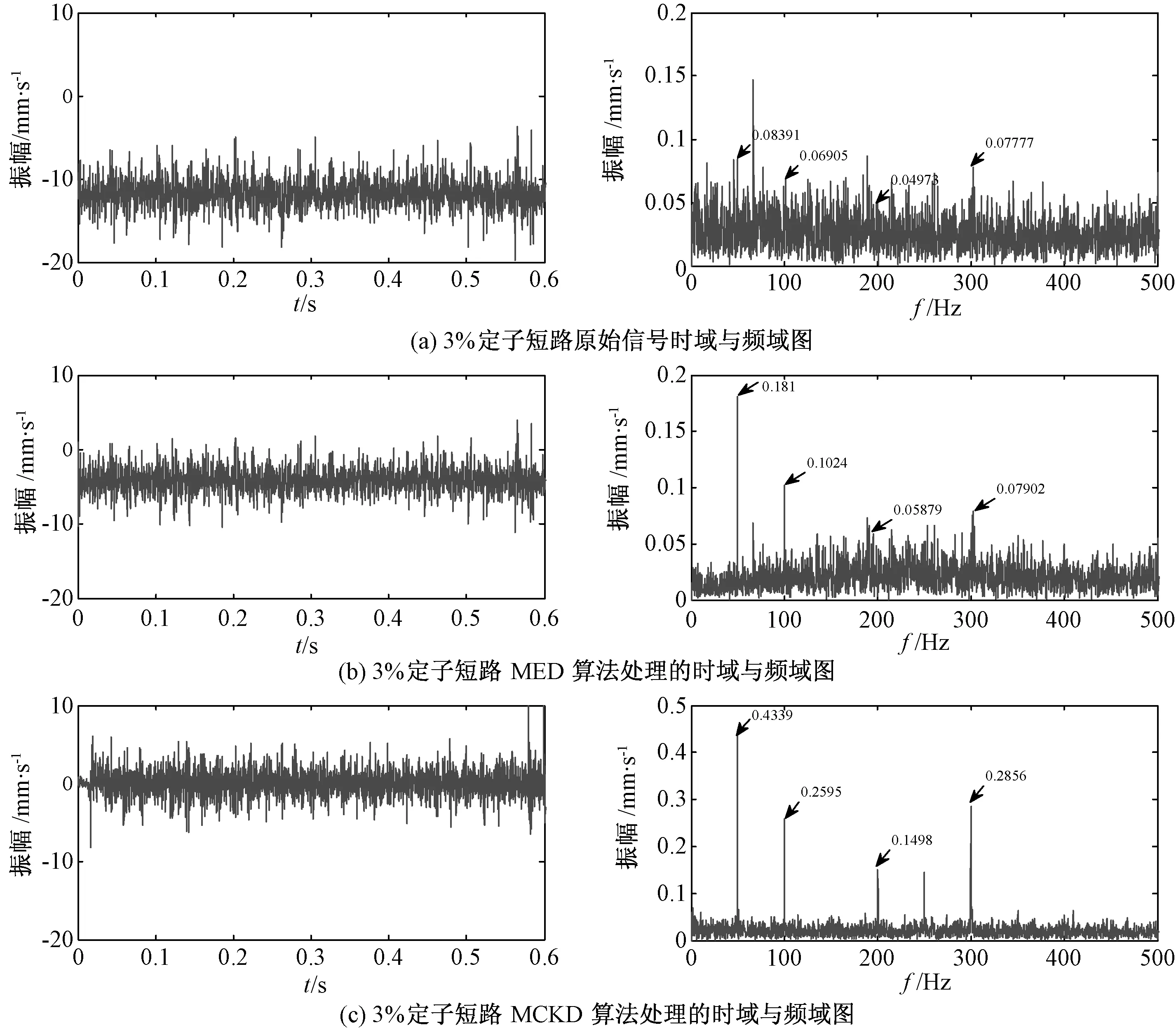
图4 3%定子匝间短路信号时域波形及频谱Fig.4 Stator vibration signal under 3% stator interturn short circuit with different processing methods

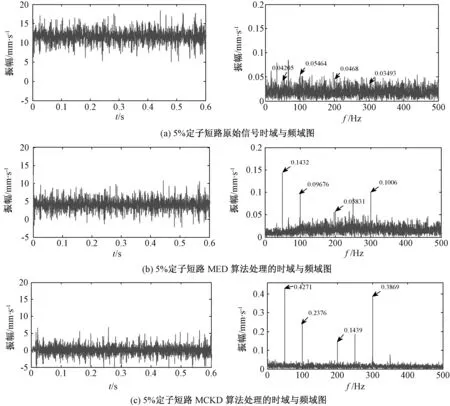
图5 5%定子匝间短路信号时域波形及频谱Fig.5 Stator vibration signal under 5% stator interturn short circuit with different processing methods

由图5可看出，经过MCKD算法处理之后，频谱图中的谱线幅值在数个倍频处(1到7倍频甚至到9倍频)都十分地明显且清晰，在二倍频、四倍频和六倍频这些故障特征频率处幅值达到了较高水平，噪声等干扰谱线较少，整个谱图相对很十分干净，故障频率特征非常明显。由此我们可以看出MCKD算法对定子正常信号频率的特征信息有十分明显的提取效果，与MED算法相比也有明显的优越性。

由于本文只对定子振动进行分析，而事实上转子的振动信号也会对定子振动产生影响，所以在基频处幅值有着明显提升。由于本文研究的是三对极电机，受到电机齿槽效应的影响，在六倍频处有比二倍频还要高的幅值，文献[19]已表明了这一结果。同时，发电机振动的影响因素太多，齿槽效应及很多未知的因素导致了五倍频处幅值也较高。因此处理结果整体上基本符合定子的振动特性。

为了更直观地将不同算法进行对比，将处理结果列表并制成折线图，具体结果见表1和图6。

由表1和图6可以看出，MCKD算法的处理效果比未处理时效果高很多，与当前主流算法MED相比也有明显的增强效果。由此可以更清楚地得出，MCKD算法能够更加清晰地提取到信号的故障信息，并与其他算法相比有明显的优越性。

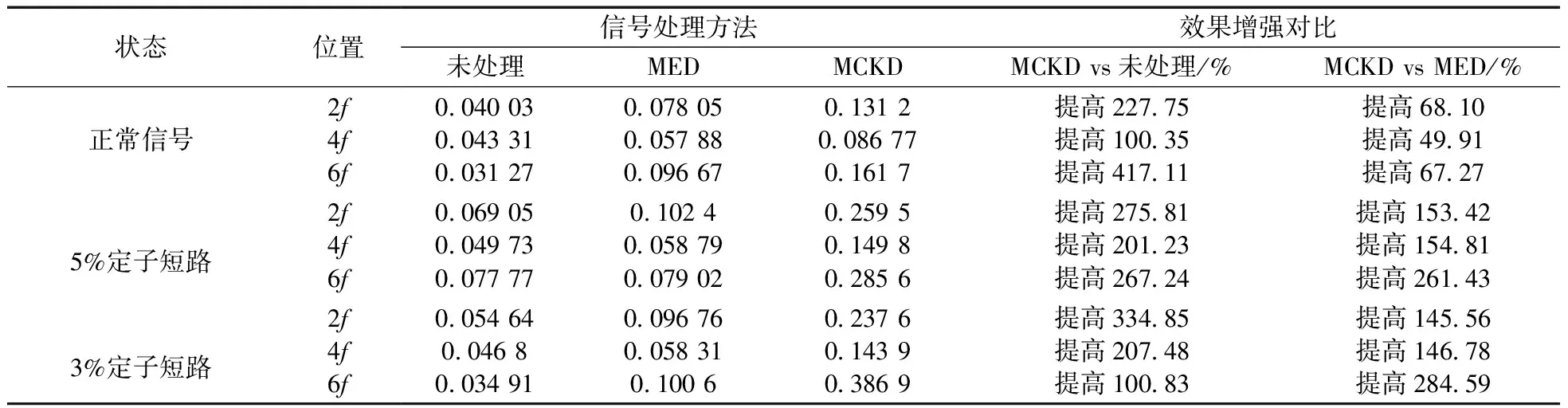
表1 MCKD与MED算法处理结果对比

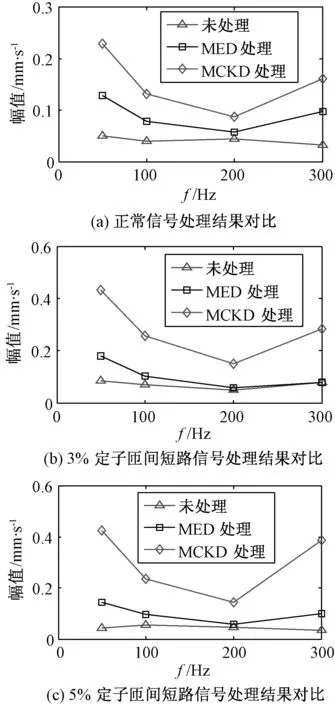
图6 原始信号、MED算法、MCKD算法处理结果对比Fig.6 Processing effect respectively for normal condition, 3% and 5% stator interturn short circuit faults

4 结 论

本文通过使用matlab对发电机定子的振动数据进行了分析，采用最大相关峭度解卷积算法和最小熵解卷积算法对信号进行了处理，获取故障前后关键故障振动特征的对比数据。本文所做的工作及得出的结论如下：

(1)以文献[15]为例，研究得到的结果中，发电机定子的特征振动信号不明显，有时甚至淹没在噪声中。因此对振动信号进行进一步的处理分析至关重要。

(2)MED算法作为当前的主流算法之一，能够有效地提取到振动信号的故障特征信息，与未处理的原始信号相比更加地清晰和明显。

(3)本文算法(MCKD)处理后，振动信号特征频率处的幅值谱线明显升高，与原始信号相比有着明显的增强，比能够有效提取故障信息的MED算法也有着很大的提升。这一结果证明了MCKD算法在发电机定子振动信号处理中的有效性和优越性。

[1] 吴继,阎革,赵秀丽，等.发电机振动原因分析及检修探讨[J].城市建设理论研究,2015,(17):6056-6057.

[2] 雷胜明,毛小明,朱华，等.发电机振动异常分析与处理[J].设备管理与维修,2012,(9):56-58.

[3] 刘奎,张冬梅,于光，等.空气耦合超声信号的小波阈值滤噪试验研究[J].机械工程学报，2015,51(20):61-66.

[4] 孙万麟,山拜 达拉拜.多模噪声背景下基于遗传小波网络的滤噪研究[J].机械设计与制造，2013,(6):190-192.

[5] 王晅,张小景,马进明，等.Contourlet域中邻域窗最优阈值滤噪算法[J].计算机工程,2010,36(5):223-224,227.

[6] 王芳,卓莉,李继红，等.基于粗集均值滤波的Hyperion高光谱数据滤噪方法[J].地理与地理信息科学,2006,22(6):30-33.

[7] 胡寿松,周川,王源，等.基于小波神经网络的组合故障模式识别[J].自动化学报,2002,28(4):540-543.

[8] 陆爽,杨斌,李萌，等.基于小波和径向基函数神经网络的滚动轴承故障模式识别[J].农业工程学报,2004,20(6):102-105.

[9] 王冰,李洪儒,许葆华，等.基于数学形态学分段分形维数的电机滚动轴承故障模式识别[J].振动与冲击,2013,32(19):28-31,92.

[10] 傅勤毅,章易程,应力军，等.滚动轴承故障特征的小波提取方法[J].机械工程学报,2001,37(2):30-32,37

[11] WANG Yanxue, XIANG Jiawei, MARKERT Richard, et al. Spectral kurtosis for fault detection, diagnosis and prognostics of rotating machines: A review with applications [J]. Mechanical Systems and Signal Processing, 2016, 66-67: 679-698.

[12] 张进,冯志鹏,褚福磊,等.滚动轴承故障特征的时间一小波能量谱提取方法[J].机械工程学报,2011,47(17):44-49.

[13] LIU Libin, LIANG Xihui, ZUO Ming J. Vibration signal modeling of a planetary gear set with transmission path effect analysis[J].Measurement, 2016(85):20-31.

[14] HE Wangpeng, DING Yin, ZI Yanyang, et al. Selesnick. Sparsity-based algorithm for detecting faults in rotating machines[J].Mechanical Systems and Signal Processing,2014(72-73):46-64.

[15] 万书亭,李和明,许兆凤,等.定子绕组匝间短路对发电机定转子径向振动特性的影响[J].中国电机工程学报,2004,24(4):157-161.

[16] 何玉灵,蒙玉超,唐贵基,等.基于正弦结构元素的自适应Top-Hat变换及发电机特征振动信号增强检测[J].中国电机工程学报,2016, 36(15):4266-4273.

[17] 王志坚,韩振南,刘邱祖，等.基于MED-EEMD的滚动轴承微弱故障特征提取[J].农业工程学报,2014,30(23):70-78.

[18] 唐贵基,王晓龙.自适应最大相关峭度解卷积方法及其在轴承早期故障诊断中的应用[J].中国电机工程学报，2015,35(6):1436-1444.

[19] 万书亭,武文姣,何玉灵,等. 振动偏心时定子绕组短路对振动特性影响分析[J]. 华北电力大学学报(自然科学版),2009,36(6):86-93.

Enhanced Detection of Generator’s Characteristic Vibration Signal Based on Maximum Correlated Kurtosis Deconvolution

HE Yuling1, WANG Ke2, ZHONG Hao1, MENG Yuchao1, WANG Xiaolong1, TANG Guiji1

(1. School of Energy Power and Mechanical Engineering, North China Electric Power University, Baoding 071003,China; 2. School of Mechatronics, Beijing Institute of Technology, Beijing 100081,China)

This paper mainly carries out the work of vibration signal processing of generator stator on the basis of maximum correlated kurtosis deconvolution (MCKD). After signal processing, time domain waveforms and frequency spectrum are obtained. Then the extracted fault feature information is used to identify the operating state of generator. To be objective, both the normal signal and the stator inter-turn short circuit fault (SISC) signal are processed by this method, which verifies the effectiveness of the method to extract fault feature of vibration signal. Compared with one of the most popular algorithms, minimum entropy deconvolution (MED), the proposed method in this paper has more convincing and accurate results of fault feature extraction. The results show that MCKD will do better than the popular algorithm in extracting fault signal feature frequency and it boosts more advantages.

generator; stator inter-turns short circuit (SISC); vibration signal; minimum entropy deconvolution (MED); maximum correlated kurtosis deconvolution (MCKD)

10.3969/j.ISSN.1007-2691.2017.03.10

2016-09-09.

国家自然科学基金资助项目(51307058)；河北省自然科学基金资助项目(E2014502052、E2015502013)；中央高校科研业务费专项基金资助项目(2015ZD27).

TM31

A

1007-2691(2017)03-0067-07

何玉灵(1984-)，男，副教授，研究方向为电站设备状态监测、控制与节能;王珂(1993-)，女，硕士研究生，研究方向为信号分析与处理；仲昊(1991-)，男，硕士研究生，研究方向为发电机状态监测与故障诊断。