大型燃煤电站回热系统抽汽流量优化研究

王惠杰，范志愿，许小刚

(华北电力大学 能源动力与机械工程学院，河北 保定 071003)



大型燃煤电站回热系统抽汽流量优化研究

王惠杰，范志愿，许小刚

(华北电力大学 能源动力与机械工程学院，河北 保定 071003)

为了提高机组热经济性，对回热系统抽汽流量进行了优化。通过理论分析，建立了级组通流特性变工况模型、级组效率变工况模型、加热器变工况模型、凝汽器变工况模型，从而能够计算全工况下的机组能耗。为了增强遗传算法的全局搜索能力，对基本遗传算法进行了改进。以改进遗传算法为优化理论，抽汽流量为优化变量，汽轮机热耗率为优化目标进行了系统整体优化。优化结果表明：热耗率优化量随着负荷的升高逐渐减小，最小优化量为22.7 kJ/(kW·h)，最大为50.1 kJ/(kW·h)。高压加热器优化后的抽汽流量均低于优化前的抽汽流量；低压加热器优化后的抽汽流量均高于优化前的抽汽流量。该方法对降低机组能耗具有一定的参考意义。

回热系统；设备变工况模型；机组能耗；抽汽流量；遗传算法

0 引 言

随着电网峰谷差的不断增大,使得越来越多的大型火电机组参与调峰任务。机组在低负荷运行时,各个设备严重偏离设计工况,使得机组的热经济性明显下降。无论在设计制造方面还是优化运行方面,机组低负荷节能都是当前亟待解决的问题。为了提高机组热经济性,现代大型机组毫无例外地采用了回热系统。作为汽轮机的主要辅助系统,回热系统对电厂的安全性、热经济性有重要的意义[1,2]。在机组运行过程中,回热系统抽汽流量的设计值仅是当加热器换热面积为设计值时的最优值。若加热器的换热面积可以被改变,则抽汽流量的设计值并非是最优值。通过动态地改变各个加热器的换热面积来调整各段抽汽流量的分布,可以在不增加设备投资的情况下使机组的热经济性进一步提高。

国内外学者对回热系统的优化运行进行了大量的研究。早期的研究主要以给水焓升为优化变量,提出了著名的雷日金法、平均分配法、几何级数分配法[1]。这些方法的推导过程中使用了大量的假设条件,其中假设所有的加热器都是混合式加热器,这与实际热力系统有很大的差别,使得推导结果不能很好地应用于实际系统。随着优化理论的不断发展,正多面体法、动态规划法、简单搜索法、非线性规划法等方法被应用于回热系统优化研究中[3,4]。使用这些方法时,为了建立优化模型必须对热力系统进行大量的简化。并且,这些方法在优化过程中容易陷入维数灾难。因此,这些方法的优化结果很难使实际热力系统在最优工况下运行。所以,这些方法也没有被广泛地应用于实际工程中。近些年来,利用遗传算法、粒子群算法等智能优化算法对回热系统优化进行了大量的研究[5-12],并且取得了一定的成果。尽管以前的研究采用了各种各样的优化方法,但是,大多数研究以抽汽压力、给水焓升、给水出口温度作为优化变量。这些方法最终都需要将回热系统的其它热力参数表示为优化变量的函数关系。由于热力系统各状态参数之间呈现明显的高维、非线性的耦合关系,所以这些变量的函数关系并不容易被描述。因此,上述方法的优化结果精度并不能得到保证。在之前的大量研究中,以抽汽流量作为优化变量的研究甚少。

本文建立了汽轮机本体、加热器、凝汽器的变工况数学模型以及机组能耗计算模型。通过改进遗传算法,以抽汽流量为优化变量、汽轮机热耗率为优化目标,对回热系统进行了整体优化。以320 MW机组回热系统为例展示了该优化方法的效果。

1 设备数学模型分析

机组在变工况条件下运行时,系统的各个热力参数都会发生变化。为了准确地描述设备运行状态,必须建立设备全工况的数学模型。

1.1 汽轮机变工况数学模型

1.1.1 级组通流特性变工况数学模型

汽轮机级组通流特性变工况数学模型为机组能耗计算模型、加热器和凝汽器变工况数学模型提供了重要的输入参数。文献[13]探究了在变工况条件下级组流量与压力、温度的关系,并提出了改进型弗留格尔公式,如式(1)所示：

(1)

式中：Ds为额定工况下的级组流量,kg/s；P0为额定工况下的级前压力,MPa；T0为额定工况下的级前温度,℃；εs为额定工况下的压比；εcs为级组临界压比。下标“1”代表变工况下的相应变量。

级组临界压比由汽轮机设备固有属性和转速决定[14]。由于本研究采用定速汽轮机,所以级组临界压比在变工况过程中为常量。而级组压比为级后压力与级前压力的比值。

机组运行过程中,级前温度比值的平方根接近于1,如图1所示。所以,可以将级前温度项在式(1)中省略。

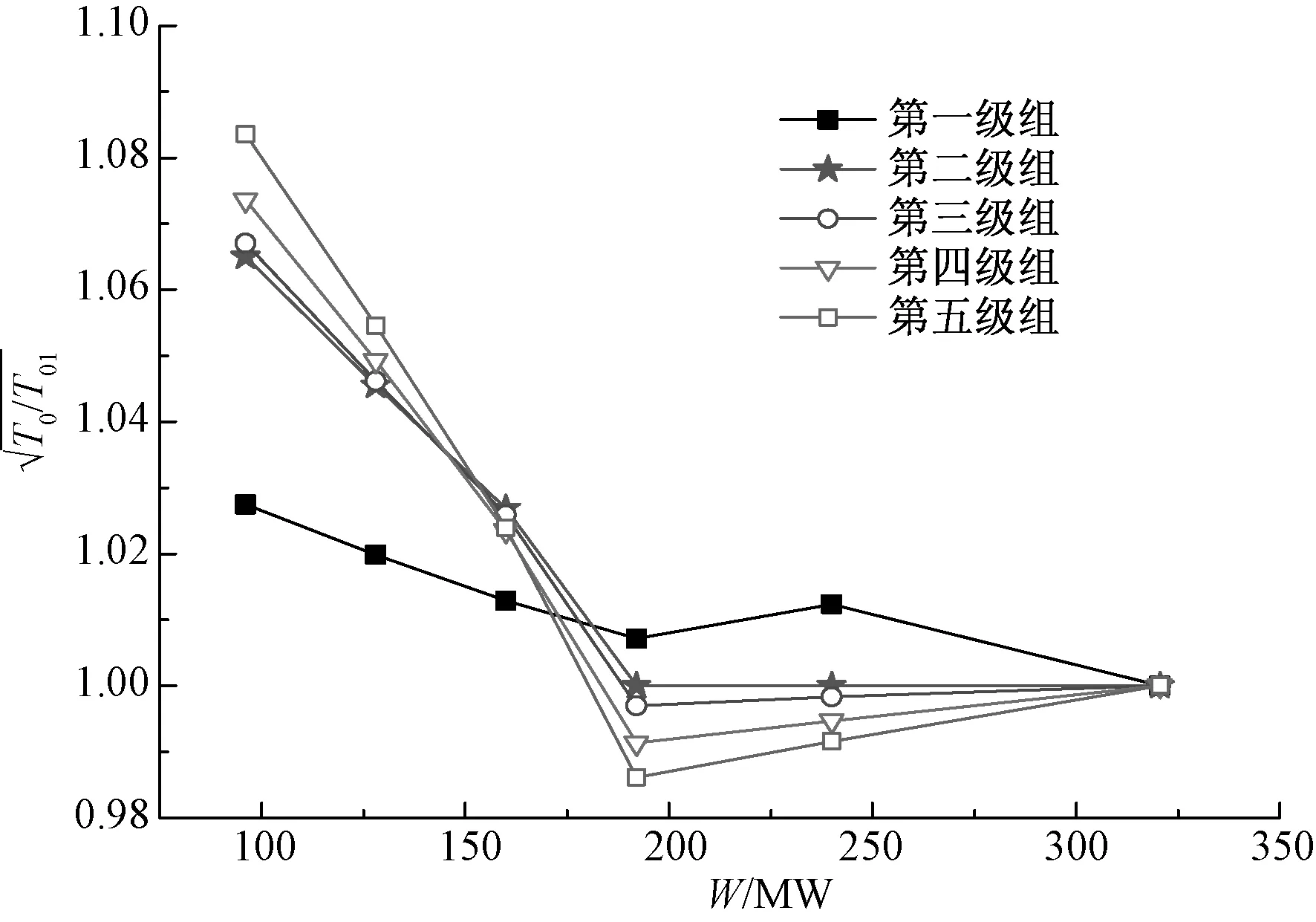
图1 变工况下级前温度变化范围Fig.1 Temperature variation range of last stage of variable condition

由上述分析可知,变工况下的级后压力如式(2)所示：

(2)

式中：P2为额定工况下的级后压力,MPa；P21为变工况下的级后压力,MPa。

在式(2)中,额定工况下的级组参数都为已知常量。所以,变工况下的级后压力是级前压力和级组流量的函数,如式(3)所示：

(3)

1.1.2 级组效率工况数学模型

机组运行过程中,级组能量损失有静叶损失、动叶损失、叶高损失、扇形损失、余速损失、漏气损失、部分进汽损失、摩擦损失、湿汽损失。

静叶损失、动叶损失、叶高损失、扇形损失由级组的几何结构决定[15]。机组运行过程中级组的几何结构不发生变化,所以上述4种损失在任何工况下都为常量。在级组的设计反动度一定时,余速损失主要由级组的理想焓降决定[15]。

漏气损失与径向间隙面积及其前后压差有关系。由于机组的叶轮设有平衡孔以及采用多级高低齿汽封装置。所以,漏气损失对效率的影响很小,可以忽略不计。

机组运行时,部分进汽损失、摩擦损失和湿汽损失对级组效率的影响较大。这三种损失主要由汽轮机转速与级组流量决定[15]。本研究采用定速汽轮机,所以三种损失只是级组流量的函数。

综上所述,级组能量损失主要由理想焓降和流量决定。级组效率为级组理想焓降和能量损失的函数。所以,级组效率的变工况数学模型如式(4)所示：

(4)

式中：η为级组效率；Δht为级组理想焓降,kJ/kg。

1.2 凝汽器变工况数学模型

机组在变工况条件下运行时,凝汽器的热负荷会发生变化。为了确定凝汽器的压力,必须建立凝汽器的变工况数学模型。

在凝汽器中蒸汽被凝结成饱和水,所以凝汽器的压力与蒸汽饱和温度具有一一对应的关系,如式(5)所示：

(5)

式中：pc为凝汽器压力,kPa；ts为蒸汽饱和温度,℃；tnw1为凝汽器冷却水入口温度,℃；Δt为冷却水温升,℃；δt为凝汽器端差,℃。

冷却水入口温度可通过温度测点得到。在凝汽器内,汽轮机排汽放热量全部被冷却水吸收,其热平衡方程如式(6)所示：

(6)

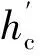
冷却水温升可由凝汽器热平衡方程推出,如式(7)所示：

(7)

(8)

将凝汽器对数平均温差表达式代入热平衡方程,可得到凝汽器端差的解析式,如式(9)所示：

(9)

文献[16]指出,凝汽器换热系数是汽轮机排汽量、冷却水入口温度、流速复杂的非线性函数。由式(8)和式(9)可知,凝汽器端差是汽轮机排汽量、冷却水流量、入口温度、流速的函数,如式(10)所示：

(10)

式中：μwl为凝汽器冷却水流速,m/s。

在凝汽器变工况范围内冷却水的密度基本为常量,所以冷却水流速只是流量的函数。因此,由上述分析可知,凝汽器变工况数学模型如式(11)所示：

(11)

1.3 加热器变工况数学模型

回热系统抽汽流量优化使加热器的运行状态偏离设计工况,必须通过变工况模型获得加热器运行参数。

1.3.1 疏水冷却段变工况数学模型

疏水冷却段总体传热系数由管内外传热系数、管内外污垢热阻、管壁导热系数、管壁厚度和换热管的内外径共同决定。管壁厚度、换热管内外径是设备固有属性。管内外污垢热阻和管壁导热系数也可认为是常量[14]。所以,疏水冷却段总体传热系数是管内外换热系数的函数,如式(12)所示：

(12)

式中：k1为疏水冷却段总体传热系数,W/(m2·K)；αs1,αt1分别为疏水冷却段壳侧、管侧对流传热系数：W/(m2·K)。

文献[14]分析相关数据,得知疏水冷却段管内外换热热阻近似相等。本文根据文献[14]的思想,利用机组设计数据统计了疏水冷却段壳侧换热系数与管侧换热系数的关系,如图2所示。

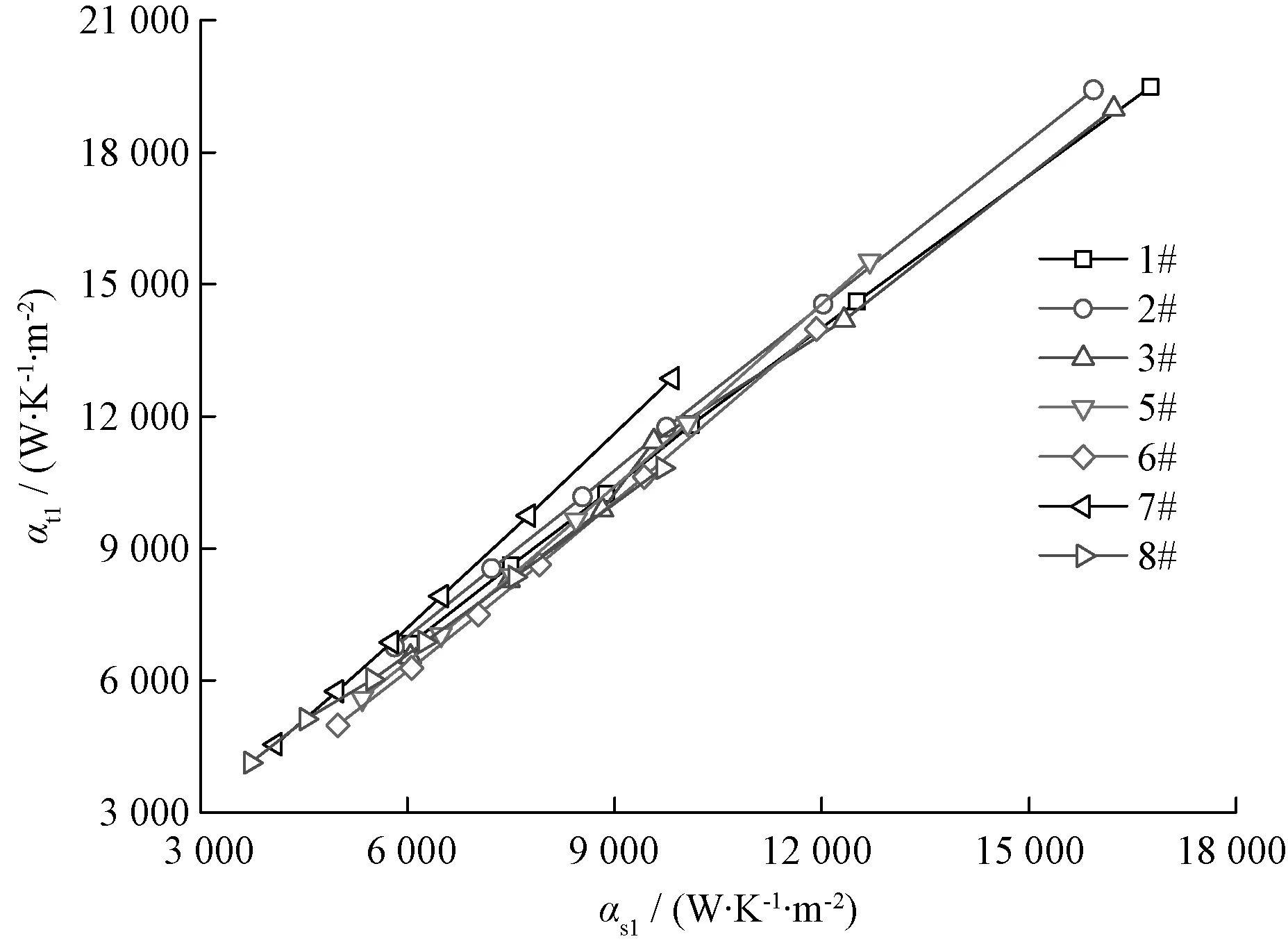
图2 管内外换热系数对比图Fig.2 Comparison of heat transfer coefficients between outside and inside tube

由图2可见,疏水冷却段壳侧换热系数与管侧换热系数近似相等,且基本成线性关系。因此,疏水冷却段总体换热系数可以用任一侧换热系数表示。本文用管侧换热系数表示总体传热系数，如式(13)所示：

(13)

文献[17]给出了管侧对流传热系数的表达式,如式(14)所示：

(14)

式中：λw为给水导热系数,W/(K·m)；Re为雷诺数；Pr为普朗特数。

将式(14)用基本物理量表示成式(15)的形式。

(15)

式中：Cpw为给水定压比热容,kJ/(kg·℃)；νw为给水运动粘度,m2/s；ρw为给水密度,kg/m3；Dwh为加热器给水流量,kg/s；Nw为一个流程内的管数。

式(15)由设备结构常数项、给水热物性系数、给水流量三部分组成。给水热物性系数由给水温度和压力共同决定。在加热器运行范围内,温度对给水热物性系数的影响比较大,而压力对给水热物性系数的影响可以忽略,如图3所示。

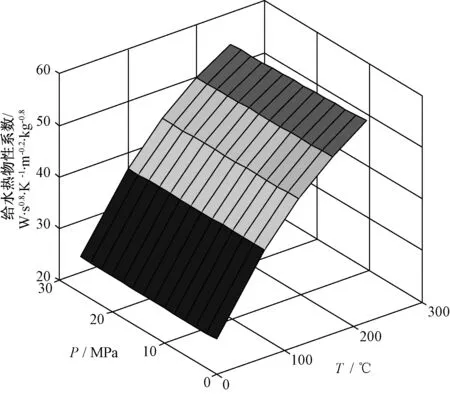
图3 压力、温度对给水热物性系数的影响Fig.3 Effect of pressure and temperature on coefficients of feed water thermal properties

综上所述,疏水冷却段管侧换热系数是给水温度和给水流量的函数,而总体传热系数是管侧传热系数的函数,如式(16)所示。

(16)

式中：tw1为给水的入口水温,℃。

疏水冷却段传热单元数为疏水冷却段传热能力系数与疏水水当量的比值,如式(17)所示:

(17)

式中：NTU1为疏水冷却段传热单元数；A1为疏水冷却段换热面积,m2；Dss为疏水流量,kg/s；Cpss为疏水定压比热容,kJ/(kg·℃)。

由式(16)可知,疏水冷却段传热能力系数为给水流量和温度的函数。疏水定压比热容主要受疏水温度的影响。所以,疏水冷却段传热单元数由给水流量、温度和疏水流量、温度决定,如式(18)所示：

(18)

式中：th为加热器的饱和温度,℃。

在疏水冷却段中,疏水水当量与给水水当量的比值小于0.1[18]。因此,疏水冷却段效能可以表示为式(19)所示的形式：

(19)

式中：ε1为疏水冷却段效能；tod为疏水出口温度,℃。

疏水冷却段的能量方程如式(20)所示：

(20)

式中：hhs为蒸汽凝结成的饱和水焓,kJ/kg；hod为疏水的出口焓,kJ/kg；t1t为疏水冷却段的给水出口温度,℃。

1.3.2 蒸汽凝结段变工况数学模型

与疏水冷却段的分析类似,蒸汽凝结段总体换热系数为管侧换热系数和壳侧换热系数的函数。并且在蒸汽凝结段中,管内的对流换热热阻相比管外的凝结换热热阻大得多。所以,蒸汽凝结段的总体换热系数为管侧换热系数的函数,如式(21)所示：

(21)

式中：k2为蒸汽凝结段总体传热系数,W/(m2·K)；αt2为蒸汽凝结段管侧传热系数,W/(m2·K)。

文献[19]给出了凝结段管内对流传热系数的经验公式,如式(22)所示：

(22)

式中：twf为给水定性温度,℃；uwh为加热器给水流速,kg/s。

在蒸汽凝结段中,给水定性温度主要受给水流量的影响[18]。在加热器运行范围内,给水密度可以视为常量,给水流速是流量的函数。所以蒸汽凝结段管侧换热系数是给水流量的函数,而总体换热系数是管侧换热系数的函数,如式(23)所示：

(23)

蒸汽凝结段的传热单元数为蒸汽凝结段的换热能力系数与给水水当量的比值,如式(24)所示：

(24)

式中：NTU2为蒸汽凝结段的传热单元数；A2为蒸汽凝结段换热面积,m2。

由式(23)可知,给水流量是传热能力系数的主要影响因素,且给水定压比热容主要受温度的影响。所以,蒸汽凝结段传热单元数是给水流量与温度的函数,如式(25)所示：

(25)

蒸汽凝结段效能如式(26)所示：

(26)

式中：ε2为蒸汽凝结段的效能；t2t为蒸汽凝结段给水出口温度,℃。

1.3.3 蒸汽冷却段变工况数学模型

在蒸汽冷却段中,过热蒸汽被冷却为饱和蒸汽。蒸汽释放的热量全部被给水吸收,能量平衡方程如式(27)所示：

(27)

式中：Di为抽汽流量,kg/s；hi,hhq分别为抽汽焓、饱和蒸汽焓,kJ/kg；tw2为加热器给水出口温度,℃。

2 机组能耗计算模型

准确的能耗计算结果才能为评价优化效果提供精确的标尺。本文以320 MW机组为例建立能耗计算模型,机组系统简化图如图4所示。

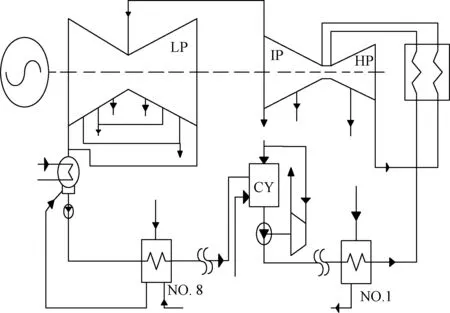
图4 320 MW机组系统简化图Fig.4 Simplified diagram of 320 MW unit system

本文将抽汽流量作为优化变量,所以汽轮机的汽水分布状态为已知量。由于汽轮机热耗率能够表征机组热经济性,所以将汽轮机热耗率作为机组能耗指标。机组能耗计算模型如式(28)所示：

(28)

式中：W为汽轮机功率,kW；Di为第i级的抽汽流量,kg/s；h0为主蒸汽焓,kJ/kg；hi为第i级的抽汽焓,kJ/kg；Wf为辅助汽流的做功量,kW；ηm为机械效率；ηg为发电机效率；Q为蒸汽吸热量kJ/h；D0为主蒸汽流量,kg/s；hfw为给水焓,kJ/kg；Drh为再热蒸汽流量,kg/s；hrh为再热热段蒸汽焓,kJ/kg；hrc为再热冷段蒸汽焓,kJ/kg；q为汽轮机热耗率,kJ/(kW·h)。

优化过程中保持主蒸汽流量不变,将第一抽汽口的热力参数作为计算起点，由汽轮机变工况数学模型可得到各级抽汽口的参数。由凝汽器变工况数学模型给出当前工况的排汽压力,配合级组效率变工况数学模型可得出汽轮机的排汽热力参数。

将汽轮机抽汽口的热力参数考虑管道压损之后便可得到各级加热器的蒸汽入口参数。

将凝汽器压力对应的饱和温度作为加热器组的计算起点。由于辅助热量本身的数值并不大,且对系统的影响较小,所以各级加热器的辅助热量取为设计值。将给水入口参数和抽汽入口参数作为加热器变工况数学模型的输入参数,可得到各级加热器的出口参数。机组能耗计算流程图如图5所示。

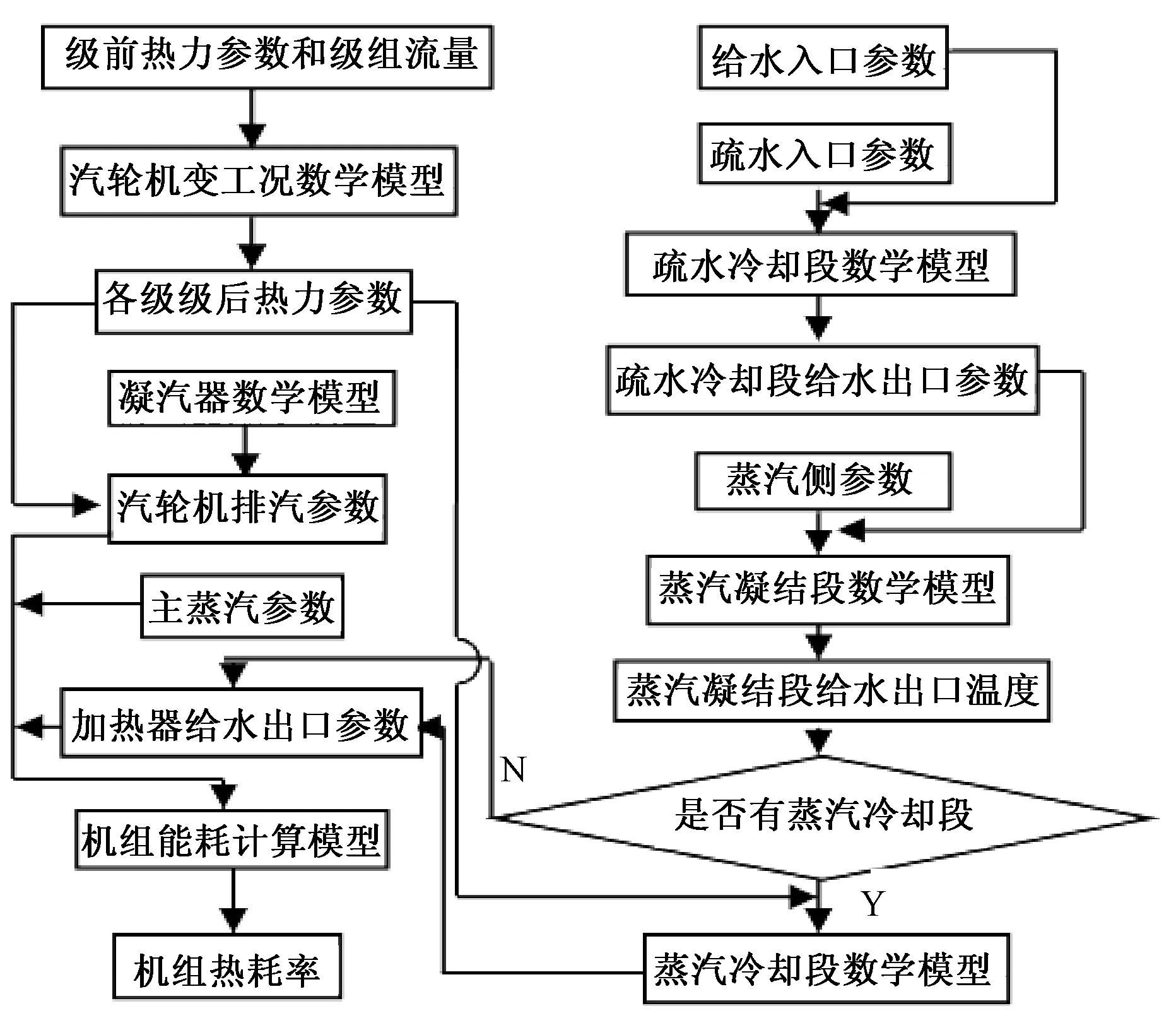
图5 能耗计算流程图Fig.5 Energy consumption calculation flow chart

将能耗计算模型应用于320 MW机组,各个工况下的模型计算值与设计值如表1所示。

由表1可见,模型计算值与设计值相对误差的最大值为0.031 3 %,能够满足工程计算要求。

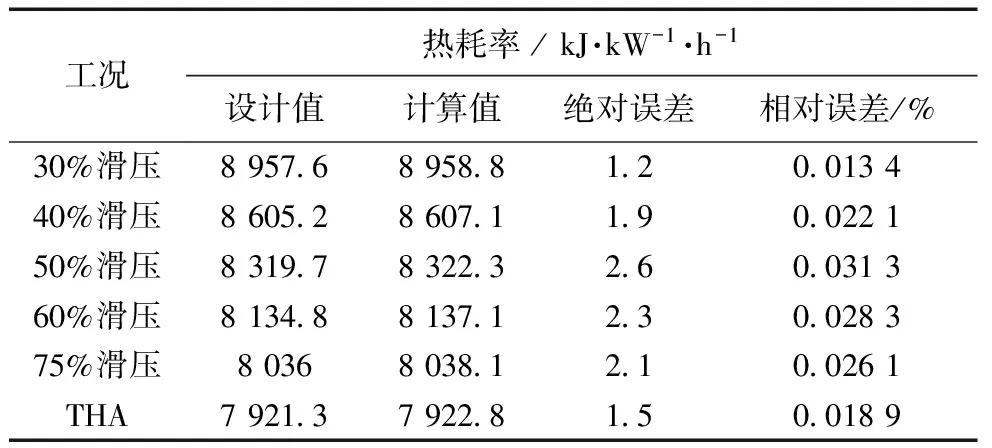
表1 机组能耗计算结果

3 系统整体优化

以图4中的国产320MW机组为例进行系统整体优化。以各级加热器抽汽流量为优化变量,汽轮机热耗率为优化目标,遗传算法为优化理论。为了增强遗传算法的全局搜索能力,对基本遗传算法进行了以下三点改进：

(1) 采用个体动态交叉概率和变异概率可以在一定程度上防止算法陷入局部极值，同时可以提高算法的收敛性能[19]。

(29)

(30)

式中：Pc为个体交叉概率；Pc1,Pc2分别为最大、最小交叉概率；Pm为个体变异概率；Pm1,Pm2分别为最大、最小变异概率；fmax为种群中最大的适应度；favg为种群平均适应度；f′为个体的适应度。

(2) 初始种群对遗传算法的全局搜索能力有较大的影响,初始种群应尽可能充满整个种群空间[20]。本文采用子空间双倍初始种群法对种群进行初始化,步骤如下：

(a) 将种群空间划分为N个子空间；

(b) 在每个子空间中随机产生2S/N个染色体；

(c) 将每个子空间中的2S/N个染色体按适应度由大到小排序。由适应度大的前S/N个染色体组成该子空间的种群。由各个子空间的种群组成初始种群。

(3) 适应度函数关系到收敛性、计算效率等多项指标。采用动态进化的适应度函数不仅可以在一定程度上保持种群多样性,还可以加快收敛速度[21]。

(31)

式中：S(x)为染色体的适应度；F(x)为染色体的函数值；[M]为不超过M的最大正整数；N为算法的迭代次数；n为当前的进化代数。

遗传算法的主要控制参数为：种群规模为100；迭代次数为1 000；最大交叉概率为0.8,最小交叉概率为0.4,最大变异概率为0.2,最小变异概率为0.05。

由机组设计数据以及数学回归分析法,拟合各个设备数学模型以便系统整体优化调用。

根据上述步骤便可进行系统整体优化。优化模型如式(32)所示。系统优化流程图如图6所示。

(32)

式中：Di,min为第i级抽汽流量的最小值,kg/s；Di,max为第i级抽汽流量的最大值,kg/s；Df为各种辅助流量,kg/s；Dfs为各个工况下辅助流量的设计值,kg/s。

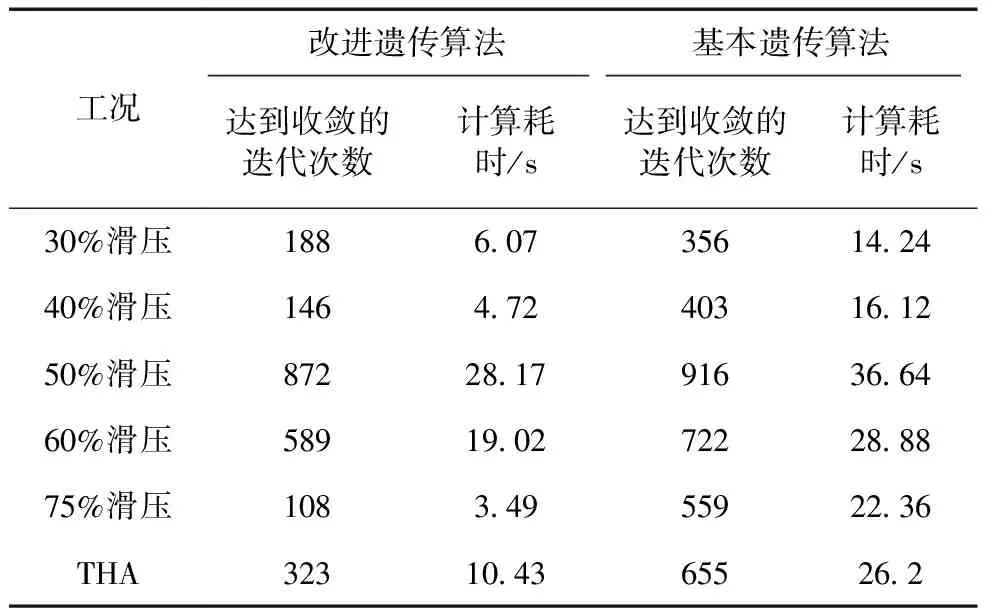
改进遗传算法和基本遗传算法的性能指标如表2所示。抽汽流量优化量与原始抽汽流量的比值定义为抽汽流量相对优化量,如表3所示。优化结果对比图如图7所示。

由表2可见,改进遗传算法比基本遗传算法达到收敛时需要的迭代次数和计算时间均有减少。因此,改进遗传算法是有效的。

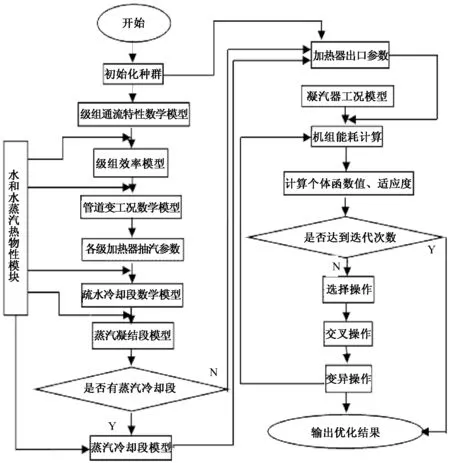
图6 系统优化流程图Fig.6 Flow chart of system optimization

Tab.2 Performance indexes of improved genetic algorithm and basic genetic algorithm

工况改进遗传算法基本遗传算法达到收敛的迭代次数计算耗时/s达到收敛的迭代次数计算耗时/s30%滑压188607356142440%滑压146472403161250%滑压8722817916366460%滑压5891902722288875%滑压1083495592236THA3231043655262

由优化结果对比图可见,热耗率优化量随着负荷地升高逐渐减小；30%工况时的热耗率优化量为50.1 kJ/(kW·h),THA工况时为22.7 kJ/(kW·h)。优化前后的各级抽汽流量均随着负荷的升高而增加。高压加热器优化后的抽汽流量在全负荷范围内均不同程度地小于优化前的抽汽流量。在机组负荷低于200 MW或高于290 MW时,除氧器优化后的抽汽流量大于优化前的抽汽流量；负荷在200 MW与290 MW之间时,优化后的抽汽流量小于优化前的抽汽流量。低压加热器优化后的抽汽流量在全负范围内均大于优化前的抽汽流量。

由于高压加热器抽汽的焓火用较大,并且抽汽与给水换热过程的温差较大,所以应该适当地使部分高加抽汽从低压段抽出,这样不仅增加了回热做功比还减小了由换热温差引起的不可逆火用损。所以,优化结果表现为高压加热器的抽汽流量减少,低压加热器抽汽流量增加。随着负荷的不断升高,越来越接近设计工况,机组性能不断上升,所以热耗率优化量不断减小。

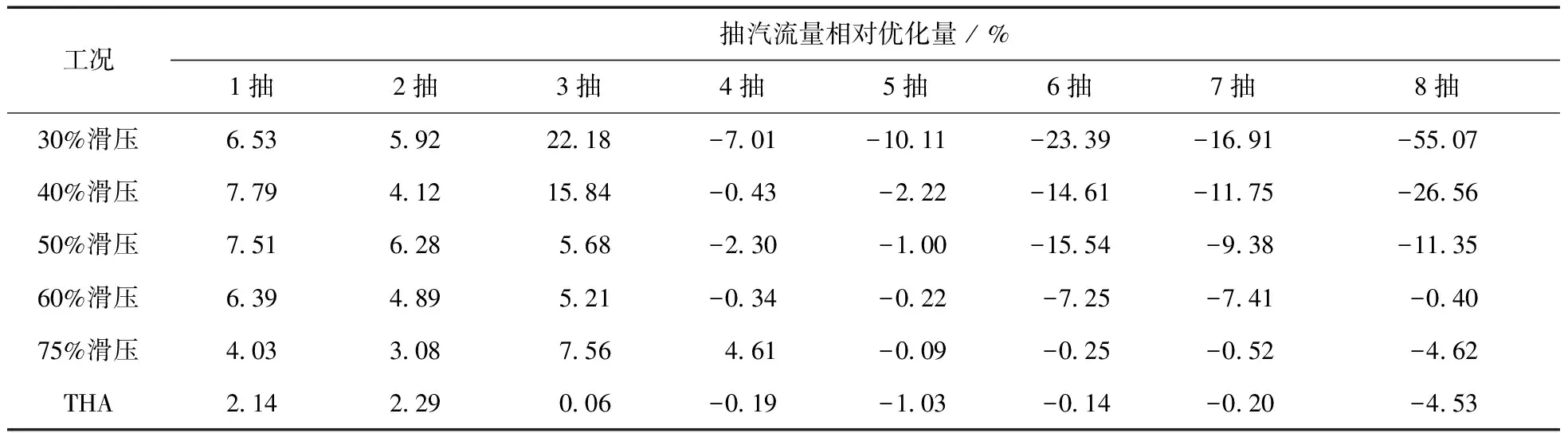
表3 抽汽流量相对优化量

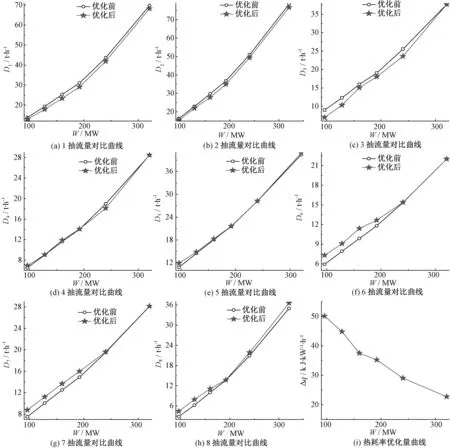
图7 优化结果对比图Fig.7 Comparison diagram of optimization results

4 结 论

(1) 通过理论分析,建立了汽轮机、回热加热器、凝汽器变工况模型、机组能耗计算模型。这些模型能够准确地描述设备运行特性,为精确的系统优化奠定基础。以遗传算法为优化理论,合理地设置优化参数,以抽汽流量为优化变量,汽轮机热耗率为优化目标,调用各个子设备模型,对320 MW机组系统进行了整体优化。

(2) 优化结果表明：机组热耗率优化量随着负荷的升高逐渐减小,最小优化量为22.7 kJ/(kW·h),最大为50.1 kJ/(kW·h)。高压加热器优化后的抽汽流量均低于优化前的抽汽流量；低压加热器优化后的抽汽流量均高于优化前的抽汽流量。

[1] 郑体宽. 热力发电厂 [M]. 北京: 中国电力出版社, 2008．

[2] LI Y, WANG C. Study on the effect of regenerative system on power type relative internal efficiency of nuclear steam turbine [J]．Energy Procedia, 2012, 17(Part A): 906-912．

[3] 郭民臣, 刘强. 火电机组热力系统给水焓升最佳分配方法 [J]. 汽轮机技术, 2008, 50(6): 422-424.

[4] 赵豹, 杨历, 高永坤, 等. 汽轮机回热系统给水焓升分配的优化和分析 [J]. 河北工业大学学报, 2013, 42(6): 100-105.

[5] 付文锋, 李飞, 王蓝婧. 除氧器和给水泵汽轮机汽源与汽轮机抽汽口的协同优化 [J]. 华北电力大学学报(自然科学版)， 2014, 41(3): 94-100.

[6] 付文锋, 王蓝婧, 李飞, 等. 基于改进动态自适应粒子群优化算法的汽轮机组给水回热分配优化方法 [J]. 动力工程学报, 2014, 34(8): 653-659．

[7] CHEN G, LU X, AMANO R S. The Optimum Assignment of the Enthalpy Rise of the Heater [C]. ASME 2003 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Chicago,USA:AMSE，2003: 1193-1201.

[8] 周兰欣, 李飞, 付文锋, 等. 基于粒子群算法的压水堆核电机组回热系统优化 [J]. 热力发电, 2014, 43(9): 5-11．

[9] BODE V V, GORE V G. Performance Analysis of Regenerative Feed Water Heating System in 270 MW Thermal Power Plant [J]. International Research Journal of Engineering and Technology, 2016, 3(4): 1180-1186.

[10] ZAHARN Z, SHI R F, LIU X J. Comparative Study on Multiobjective Power Unit Coordinated Control Problem via Differential Evolution and Particle Swarm Optimization Algorithms [J]. Advanced Materials Research, 2013, 650: 470-475.

[11] 曹凯, 陈国虎, 江桦, 等. 自适应引导进化遗传算法 [J]. 电子与信息学报, 2014, 36(8): 1884-1890．

[12] YANG Z L, DAI Z G, WANG T B. Feed-Water Enthalpy Rise Optimum Distribution Mechanism Model of PWR Nuclear Power Unit Based onGenetic Algorithm [J]. Advanced Materials Research, 2014, 1008- 1009 : 231-236.

[13] 张春发, 崔映红, 杨文滨, 等. 汽轮机组临界状态判别定理及改进型Flugel公式 [J]. 中国科学(E辑), 2003, 33(3): 264-272．

[14] 王惠杰. 基于混合模型的机组状态重构及运行优化研究 [D]. 保定：华北电力大学, 2009.

[15] 胥传普, 汪孟乐. 汽机中间级组全工况损失与效率仿真模型 [J]. 华东电力, 1988, (1): 43-46．

[16] 沈士一. 汽轮机原理 [M]. 北京: 中国电力出版社, 1992.

[17] 闫水保. 电厂热力系统节能分析方法研究 [D]. 南京: 东南大学, 2002.

[18] 杨涛, 胥建群, 周克毅, 等. 考虑水位影响的蒸汽动力发电机组给水加热器变工况特性 [J]. 中国电机工程学报, 2014, 34(2) : 231-239.

[19] 蔡锡琮. 高压给水加热器 [M]. 北京: 水利水电出版社, 1995.

[20] 彭帅英, 李光杰, 彭文, 等. 基于改进遗传算法的Holt-Winters模型在踩空沉陷预测中的应用 [J]. 吉林大学学报(地球科学版), 2013, 43(2): 515-520.

[21] 李宁, 王李管, 贾明涛, 等. 改进遗传算法和支持向量机的岩体结构面聚类分析 [J]. 岩土力学, 2014, 35(S2): 405-411.

[22] 张思才, 张方晓. 一种遗传算法适应度函数的改进方法 [J]. 计算机应用于软件, 2006, 23(2): 108-110．

Research on Optimization of Extraction Steam Flow of Regenerative System in Large Scale Coal Fired Power Plant

WANG Huijie,FAN Zhiyuan,XU Xiaogang

(School of Energy Power and Mechanical Engineering, North China Electric Power University, Baoding 071003, China)

Extraction steam flow of regenerative system was optimized to improve the thermal economy of unit. Some models were established on the basis of theoretical analysis. There were variable operating condition models of the flow characteristics and efficiency for the stage group of turbine and variable operating condition models of the heater and condenser. The unit energy consumption under full operating conditions can be calculated by these models. The basic genetic algorithm was improved in order to enhance the global searching ability. Overall optimization of the system was carried out on the basis of improved genetic algorithm. In this process, the extraction steam flow was the optimization variable, and the heat consumption rate of the steam turbine was optimization objective. The optimization results show that the optimized amount of heat consumption rate decreases as the load increases. The minimal optimized amount of heat consumption is 22.7 kJ/(kW·h) while the maximum is 50.1 kJ/(kW·h). Optimized extraction steam flow of high pressure heater is lower than the original one. While optimized extraction steam flow of low pressure heater is higher than original flow rate. This method has a certain reference value for reducing the energy consumption of the unit.

regenerative system; variable operating condition model for the equipment; unit energy consumption; extraction steam flow; genetic algorithm

10.3969/j.ISSN.1007-2691.2017.03.13

2016-06-16.

北京市自然科学基金资助项目(3132028).

TK 284.1

A

1007-2691(2017)03-0090-09

王惠杰(1972-),男,副教授,主要从事能源利用与节能技术、热力发电厂系统、设备及运行节能在线监测及指导系统的研究与开发工作。