一道题 一节课——“用长方形纸卷圆柱”教学思考

◇刘利利

一道题 一节课
——“用长方形纸卷圆柱”教学思考

◇刘利利

作为一名数学教师，一道数学题上一节课的经历大家可能都经历过，无外乎换个情境、换个数据变换着形式边讲边练。然而，这里所说的“一道题”是指北师大版教材六年级下册第一单元“圆柱与圆锥”中练习一的第12题（如图1）。

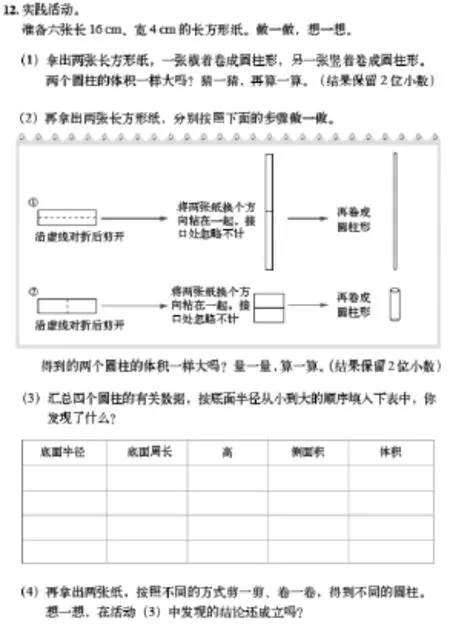
图1

面对这样一道题——一道实践活动题，我们应该怎样做呢？是学生先回家自己操作，然后教师课上订正、交流呢？还是教师先在课上讲解一下，再让学生回家去操作呢？我想以上的做法都过于简单、草率，都是为了做题而做题。

这道题给我们提供了一个特别好的实践活动素材。小学数学实践活动是培养学生综合数学能力的重要途径。如果我们的数学教学忽视了实践或实践不到位，便有可能成为无本之木、无源之水。

回到上面的这个问题，如果只是让学生在大量的计算中，寻找体积间变化的规律，显然违背了此题的意图，即鼓励学生应用所学的圆柱的表面积和体积的知识，经历探索规律的过程，体会一些变量之间的关系。我们应该单独用一节课的时间开展教学，组织学生展开充分的活动，并进行交流，发展学生的空间观念、应用意识和创新能力。基于以上想法，我们就把这节课研发成了一节有意思的综合实践课。

一、创设有意思的问题情境，培养应用意识

选择一个什么样的情境是设计本节课的一个首要的问题。我们组的几位老师进行了一次头脑风暴：通风管、下水管、吸管、套袖……我们绞尽脑汁想了许多生活中的圆柱模型，想出一个否定一个，由于牵扯的知识面广而复杂，我们争得面红耳赤。

争论中，有位老师灵机一动，提议：能不能围粮仓，真的让学生装粮食呢？这样可以让学生在操作验证的过程中感受、体会数学在生活中的应用，真正在课堂上动起来。一个有意思的、学生感兴趣的情境，可以激发学生解决问题的欲望，发展其应用意识。因此用长方形纸围立体粮仓装大米的情境应运而生。

二、精心组织实践操作活动，发展创新意识

情境有了，几位老师迫不及待地动起来。有的人设计长方形纸的大小，还有的人拿出了自己带的“苦荞”茶当大米……真是不做不知道！同样一张纸围的方式不同（如图2），体积的差别如此之大！视觉上的冲击远比数据上的冲击要大得多！那种兴奋和体验无法用言语表达。我想这就是实践的魅力！因此更加坚定了我们把这道题上成一节课的信念。同时，我们给本节课起了一个响亮的课题名：挑战不可能。

图2

于是我们为学生创设了一个“问题场”，给予他们足够的时间去操作、去实践，在实践中发现问题，并探究思考解决问题的方案。

教学片段一：发现不可能。

教师课件出示：用一张长10厘米、宽6厘米的长方形纸围一个立体图形（接口处忽略不计，结果保留一位小数），想把体积为90立方厘米的大米装下。

师：猜想一下，能装下吗？

生：不能装下。

生：能装下吧。

（学生有点儿犹豫）

师：到底能不能？怎么办呀？

生：我们想动手试试。

师：需要什么操作材料呢？

生：大米、纸、胶条、剪刀……

（学生四人一组进行活动，教师巡视，并对操作困难的小组进行指导，而后组织全班进行交流）

师：你们是怎么研究的？有什么发现？

（学生边演示边叙述，教师把学生的方法板书在黑板上）

方法1：沿长方形的长卷成高为6厘米的圆柱，体积约为47.8立方厘米。

方法2：沿长方形的宽卷成高为10厘米的圆柱，体积约为28.7立方厘米。

方法3：沿长方形的长围成底面为正方形，高为6厘米的长方体，体积为37.5立方厘米。

方法4：沿长方形的宽围成底面为正方形，高为10厘米的长方体，体积为22.5立方厘米。

师：回顾一下，这个活动我们是怎么进行的，经历了哪些过程？

生：猜想—实践—结论。

师：通过操作、计算，我们发现用这张纸围成的立体图形中，底面周长为10厘米的圆柱体积是最大的。它能装下这些大米吗？

生：不能装下。

生：看来这个任务不可能完成了。

师:换一个角度思考问题，也许不可能就变成可能了，你们想试试吗？

（激发学生继续研究的欲望）

生：想！

师：我们一起来挑战。

在这个活动中，我们希望学生通过操作先直观感受到“装不下”。思考后还能发现：用长方形纸的长边当作底面周长时，圆柱的体积比较大。当大多数学生都认为不可能装下时，教师适时提出疑问，为学生提供思考的另一扇窗，鼓励学生继续探究下去，激发学生探究的欲望。

教学片段二：挑战不可能。

出示：用一张长 10厘米、宽6厘米的长方形纸围一个圆柱，想把体积为90立方厘米的大米装下。

师：你们想想怎么办。

（学生独立思考，有的学生皱起了眉头）

师：你们有什么困难？

生：刚才我们围成的立体图形中圆柱的体积最大，我们试过了，没法装下这些大米，还能怎么办呢？

生：没准能装下，可以剪开试试。

师：你怎么想到剪开的呢？

生：刚才已经证明长边当底面周长围出的圆柱体体积最大，结果装不下，只有剪开尝试一下，也许会有希望。

师：下面我们就试试看。我给你们每个组准备了一张活动记录单，请你们边活动边把过程记录在这张纸上。

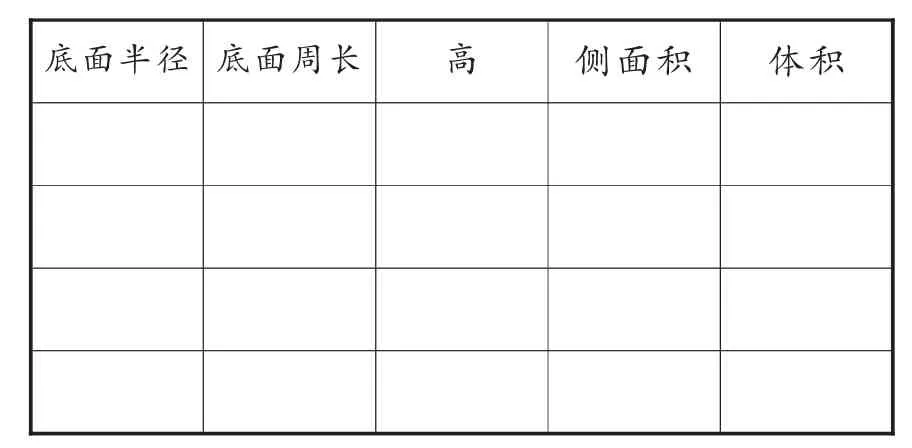
表1 活动记录单

（学生小组活动，教师巡视，并对操作困难的小组进行指导，而后组织全班讨论）

师：你们是怎么研究的？说说你们的研究过程。

（学生的方法大致有以下几种）

方法1：沿着长对折，剪开、拼接，围成底面周长为20厘米、高为3厘米的圆柱（如图3），体积约为95.5立方厘米。

方法2：沿着长折成3等份，剪开、拼接，围成底面周长为 30厘米、高为2厘米的圆柱（如图4），体积约为143.3立方厘米。

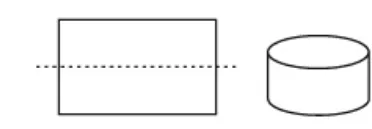
图3

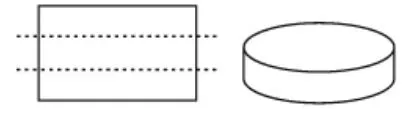
图4

方法3：沿着长折成4等份，剪开、拼接，围成底面周长为40厘米、高为1.5厘米的圆柱 （如图5），体积约为191.1立方厘米。

方法4：沿着宽对折，剪开、拼接，围成底面周长为12厘米、高为5厘米的圆柱（如图6），体积约为57.3立方厘米。

方法5：沿着宽折成3等份，剪开、拼接，围成底面周长为18厘米、高为厘米的圆柱（如图7），体积约为86.0立方厘米。

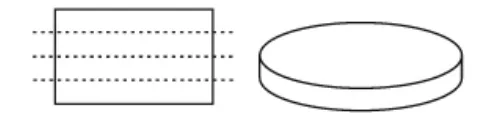
图5

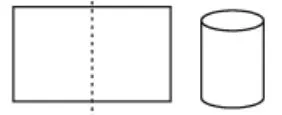
图6

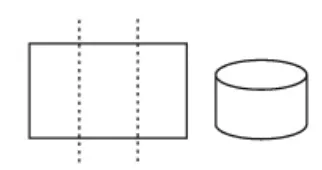
图7

……

当学生发出“没准能装下，可以剪开试试”的心声时，一石激起千层浪，教师带领学生开始挑战不可能，想办法把不可能变成可能。在小组操作结束后，很多学生都兴奋地击掌祝贺自己实验成功，并发现“当圆柱侧面积相同时，底面半径越大，高越小，体积越大”“当侧面积相同时，越是细长的圆柱体积越小，越是粗矮的圆柱体积越大”，等等。

三、关注学生发展，让不同的学生有不同的收获

每个学生都是不相同的。课上我们为学生创设了一个思考的平台，给予充分时间让他们进行自我反思和提升。他们的收获是多元的，不再拘泥于知识的掌握。看看下面学生课后的一些想法和收获。

小组内自发合作、自觉分工，在活动中配合得越来越默契（如图8）。

图8

很多学生在倒米的时候想到自制漏斗,能够运用已有的生活经验（如图9）。

图9

有的学生测量出一粒大米的高，把底面周长尽可能扩大，并且猜想如果装的是水而不是米，装得一定更多（如图10）。这不就是极限思想吗？

图10

在带领学生实践的过程中，我深刻体会到数学实践活动不仅让学生主动获取知识，还促使学生发现和研究问题，增强了学生运用数学的意识，激发了学生的创造潜能，培养了学生的创新精神。

（作者单位：中国农业大学附属小学）