基于波传播法的椭圆柱壳自由振动特性研究

张冠军, 朱 翔, 李天匀, 缪宇跃

(华中科技大学 船舶与海洋工程学院， 武汉 430074)

基于波传播法的椭圆柱壳自由振动特性研究

张冠军, 朱 翔, 李天匀, 缪宇跃

(华中科技大学 船舶与海洋工程学院， 武汉 430074)

基于Flügge壳体理论推导出椭圆柱壳的自由振动方程。由于椭圆柱壳周向曲率的变化，造成振动方程在周向模态阶数域内不解耦，采用波传播法将壳体位移以双Fourier级数形式展开，椭圆截面曲率半径以单Fourier级数形式展开，通过级数变换，将变系数的偏微分方程组转换为关于周向模态阶数相互耦合的有限阶常系数线性方程组，通过求解耦合振动方程得到椭圆柱壳的固有频率。随后对影响壳体固有频率的主要参数进行分析，得到椭圆柱壳对称和反对称模态频率随椭圆度、壳长比等参数的变化规律。

椭圆柱壳；自由振动；固有频率；椭圆度参数；反对称模态

随着加工技术的进步，椭圆柱壳在潜器、航空航天、管道输送等领域的应用日益增多。相比于圆柱壳结构，椭圆柱壳在潜器、航空器仓容及设备布置上具有更大优势，椭圆形管道相对于方形管道断面湿周面积小，密闭性更好，相对于圆形管道占用高度空间小。另一方面，即使是针对原设计的圆柱壳结构，由于制造工艺、加工方法或焊接变形，乃至巨大的深水压力作用等诸多因素的影响，其横截面也无法保证为一个完美的圆形，不可避免的存在各种几何缺陷，可能产生不可忽略的椭圆度等偏差[1-2]。因此，研究椭圆柱壳的自由振动特性具有重要意义。

目前在结构工程领域对于圆柱壳体的振动特性研究较为全面，其相关文献也较多，而对于椭圆柱壳振动方面的研究还相对较少。由于椭圆柱壳周向曲率的改变导致其振动方程是一个变系数的偏微分方程组，因此无法像圆柱壳那样可以得到解析解，只能借助于各种数值解法进行求解，而其方程又颇为繁琐，给求解带来了诸多不便。Klosner[3-4]最早运用摄动解法对椭圆柱壳自由振动特性进行了研究，但其方法仅适用于椭圆度较小的情况，应用范围受到限制。随后Culberson和Boyd等[5-6]利用部分简化后的Love理论和Donnel理论研究了椭圆柱壳的自由振动，但简化使得求解壳体低频频率及计算较长的壳体频率时，其结果存在较大误差。Elsbernd等[7]采用变分法对具有初始应力的椭圆柱壳进行了研究，其方程形式颇为繁琐复杂，应用起来并不方便，且其只对特定的椭圆度进行了计算，没有深入讨论固有频率与椭圆度之间的关系。朱建雄等[8]使用了一种特殊的坐标变换将复杂截面形状的柱壳映射成圆柱壳，通过对变化后的圆柱壳进行相关的振动分析可以近似求得非圆截面柱壳在不同边界条件下的频率及振型，但该方法中结果的准确性依赖于映射形状函数节点数的选取，而节点数越多则公式推导及计算越复杂，且该方法涉及大量导数求积及高斯数值积分，使用上存在一定局限性。最近，Khalifa[9]基于Flügge壳体理论，采用传递矩阵法研究了支撑在弹性地基上的正交各向异性椭圆柱壳的自由振动特性，讨论了壳体及地基相关参数对椭圆柱壳振动特性的影响。Ahmed等[10]同样采用传递矩阵法研究了周向变厚度椭圆柱壳的自由振动特性。但传递矩阵法受单元传递矩阵的计算精度、传递矩阵连乘过程中的累积误差以及计算机的舍入(或截断)误差影响，状态向量在传递过程中会产生一定的精度损失，对于指数矩阵还存在收敛稳定性问题，且计算效率较低[11]。最近张盛等用有限元软件对包括具有初始椭圆度在内的几种含有几何制造误差的圆柱壳的声振特性进行了仿真分析和计算。Tornabene等[12]采用一种和有限元法类似的广义积分法求解了复合材料椭圆柱壳的自由振动特性。Namazi等[13]采用有限元法与实验法研究了复合材料椭球壳的自由振动特性，并将有限元法结果与实验结果进行对比，结果吻合较好，同时研究了材料参数及结构参数对椭球壳自由振动的影响。

本文基于Flügge[14]的壳体理论，采用波传播法并结合Marguerre[15]对非圆截面曲率半径的处理方法对壳体的自由振动方程进行了推导，将变系数的偏微分方程组转换为周向模态阶数相互耦合的有限阶常系数线性方程组进行求解，得到椭圆柱壳的固有频率及振型。通过与已有文献结果对比，证明了本文处理椭圆柱壳周向变曲率的方法以及理论建模和求解方法的有效性。其后进行了更加深入的研究，分析讨论了椭圆度和壳长L/mr0比对壳体对称和反对称模态频率的影响。

1 研究对象

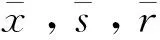
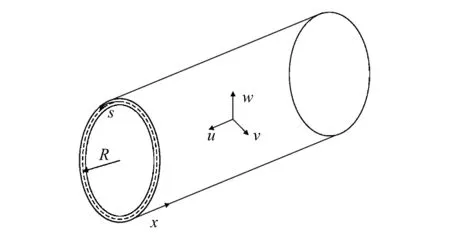
图1 椭圆柱壳几何参数及坐标系Fig.1 Geometry parameters and coordinate system of elliptic cylindrical shell

现引入下列无量纲坐标:

(1)

2 基本理论推导

2.1 壳体的位移及内力基本关系

根据Flügge薄壳理论，壳体的几何方程为：

(2)

式中：εx和εs为壳体中面内各点的线应变;γxs为剪应变;κx,κs和τ为中面内各点主曲率及扭率的改变。

壳体的物理方程为:

(3)

式中：K=Eh/(1-μ2)为壳体的拉压刚度;D=Eh3/12(1-μ2)为壳体的弯曲刚度；Nx,Ns分别为x和s方向单位宽度上的面内力；Nsx和Nxs为平面内单位宽度上的剪切力；Mx,Ms和Mxs,Msx分别为单位宽度上的弯矩和扭矩。

壳体内的静力平衡方程为：

(4)

式中：Qx和Qs分别为x和s方向单位宽度上的横剪力。

将式(4)中第4式和第5式代入到第2式和第3式并联立第1式，可得到一组新的平衡方程：

(5)

将式(2),式(3)代入式(5)中，可得到矩阵形式表达的关于位移变量的平衡方程：

(6)

其中各算子表达式如下：

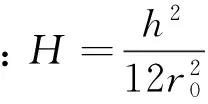
2.2 真空中椭圆柱壳体的自由振动方程

为进一步求解式(6)，需将Lij(i,j=1,2,3)转变为常系数的偏微分形式。首先需要给出椭圆柱壳截面的曲率半径r(s)的具体表达式。Marguerre首先提出了用傅里叶级数表示非圆截面曲率半径的方法。随后，Romano等[16]将Marguerre的方法进行了简化，只取其傅里叶级数的前两项来表示椭圆截面的曲率半径，其无量纲表达式如下：

(7)

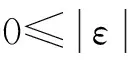
ε=3Q-36/35Q3

(8)

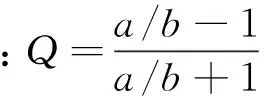
圆柱壳在周向有无数条对称轴，其对称模态和反对称模态的振型相同，可偏转一定角度重合。对于椭圆柱壳，只有长轴和短轴两条对称轴，有必要分别讨论对称与反对称模态的变化规律(本文中所讨论椭圆柱壳的对称与反对称模态均相对于长轴)。将壳体各位移在轴向和周向展开成双Fourier级数的形式。对于对称模态，其展开形式为

(9)

对于反对称模态，其展开形式为

(10)

式中：m是轴向半波数；n是周向模态阶数；Um,n,Vm,n,Wm,n为不同m，n下壳体轴向、周向和径向位移Fourier幅值系数；km为壳体的轴向半波数，不同边界条件下km的可根据梁函数推导出其近似值[17]。需要指出的是基于波传播法的位移展开形式对于简支边界条件，长壳短壳均适用，但其它边界条件则主要适用于中长壳。如果在壳体轴向位移函数假设形式上采用Fourier级数扩展形式，则对于短壳也可以扩展到任意边界。

将式(7)和式(9)代入到平衡方程式(6)中，通过级数变换可将式(6)中的变系数转变为常系数，得到三个关于Um,n,Vm,n,Wm,n沿周向模态阶数n相互耦合新的方程

(11)

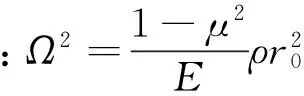
3 数值计算及分析

进一步考察式(11)可知，式(11)中的Um,n,Vm,n,Wm,n关于不同周向模态阶数n是相互耦合的，且n均为奇数或偶数。表明式(11)中，n的奇数项与偶数项是非耦合的，则Um,n,Vm,n,Wm,n可以根据n的奇偶数性分开求解。对于任意给定的轴向半波数m，Um,n,Vm,n,Wm,n都可以按n的奇偶值分成两组，由于椭圆度ε的影响，每一组中Um,n,Vm,n,Wm,n又会相互耦合成无穷多个线性方程，需对方程组进行截断求解，截取的项数与解的精确度有关。

当n取有限项p时，可以得到3p个线形方程(m>0)，并写成矩阵形式：

[M(q)-Ω2I]X(q)=0(q=1,2)

(12)

式中：X(1)[Um,1Um,3…Um,2p-1⋮Vm,1Vm,3…Vm,2p-1⋮Wm,1Wm,3…Wm,2p-1],对应于n取奇数；X(2)[Um,0Um,2…Um,2p-2⋮Vm,2Vm,4…Vm,2p-2⋮Wm,0Wm,2…Wm,2p-2]，对应于n取偶数。

M(q)(q=1,2)为3p阶的实数方阵，由式(11)中的系数循环迭代而成，I为单位矩阵，0表示零向量。

为满足式(12)中的X(q)有非零解，则要求：

(13)

求解式(13)可得椭圆柱壳的固有频率。

3.1 收敛性分析

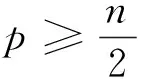
这里选取周向模态阶数n=10进行分析，利用QR分解法求解式(13)，得到真空中椭圆柱壳的自振频率。计算的模型参数：壳厚比h/r0=1/100，泊松比μ=0.3，杨氏模量E=2.1×1011Pa，材料密度ρs=7 800 kg/m3，壳体两端简支。在后文关于不同椭圆度椭圆柱壳的对比分析及椭圆柱壳与圆柱壳的对比中，壳体的平均半径r0是相等的，即壳体的截面周长是相等的。椭圆柱壳固有频率随截断项数变化的计算结果,如图 2 所示。

图2 无量纲固有频率随截断项数的变化(n=1)Fig.2 Dimensionless natural frequency changes with the truncated number(n=1)

从图2可知，随着截断项数p的增加，椭圆柱壳固有频率最终会趋于稳定，即表明计算结果趋于收敛。当壳体椭圆度较小时，计算结果趋于收敛所需的截断项数相对较少，当椭圆度较大时，则需更高的截断项数以保证结果收敛。随着截断项数的增加，计算结果的精度也会更高，但过多的截断项数会导致计算效率的降低，在n=10，L/mr0≤20范围内，取截断项数p=25可以保证足够的精度。通过计算发现，在其它周向模态阶数(包括奇数阶数和偶数阶数)下的收敛性情况都也都大体一致，因此在本文后续的计算中取p=25。

3.2 数值方法及验证

为了验证本文计算方法及程序的可靠性，同基于变分原理进行求解椭圆柱壳固有频率的文献[7]结果进行了对比，如表1所示。从表1可知，两者结果吻合很好，证明了本方法的准确性与可靠性。

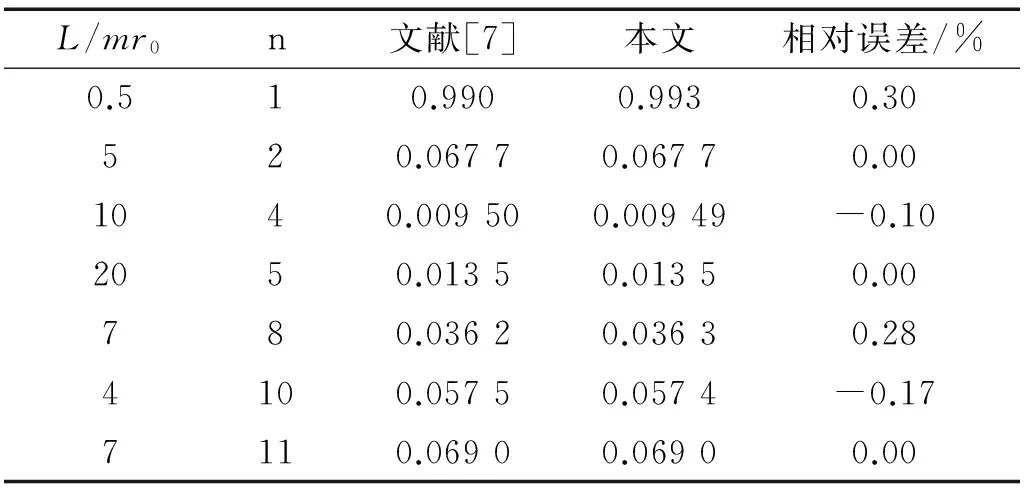
表1 椭圆柱壳的无量纲固有频率Ω对比验证 (h/r0=0.002，μ=0.3,ε=0.5，E=2.1×1011，两端简支)Tab.1 Dimensionless natural frequency verification and comparison of elliptic cylindrical shell (h/r0=0.002，μ=0.3,ε=0.5，E=2.1×1011， Simply supported-Simply supported)

3.3 椭圆柱壳模态振型

圆柱壳有无数条对称轴，且对称和反对称振型可

通过偏转重合，而椭圆柱壳只有长轴和短轴两条对称轴，其对称振型和反对称振型不同，因此，有必要对椭圆柱壳的对称振型和反对称振型进行研究。

图3给出了不同周向模态阶数下椭圆柱壳的横截面振型图，可以看出除周向模态阶数n=0以外，其他周向模态阶数均存在振型明显不同的对称模态和反对称模态。

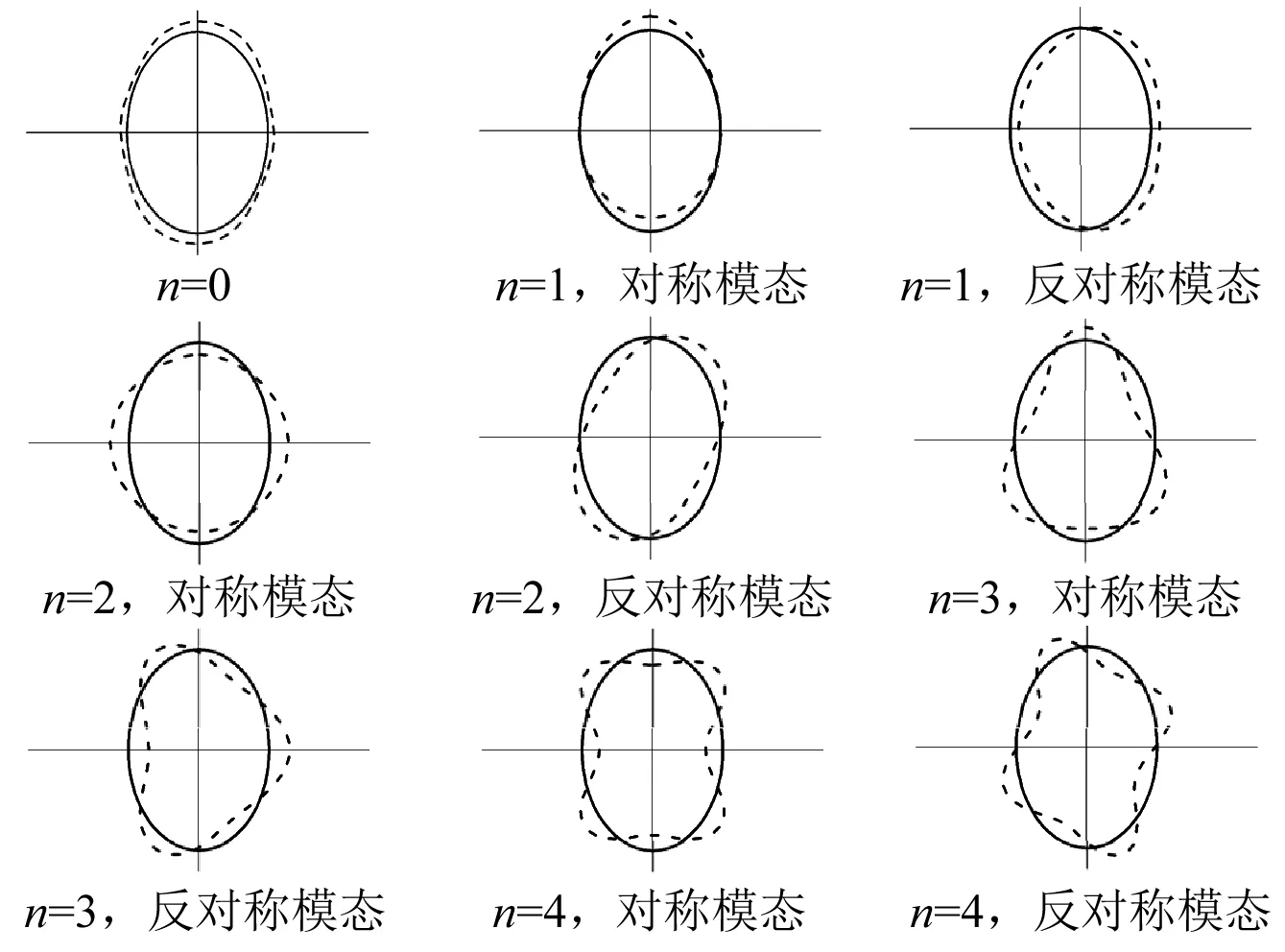
图3 椭圆柱壳模态振型图Fig.3 Mode shape of elliptic cylindrical shell

3.4 椭圆柱壳固有频率随壳体参数的变化

3.4.1 壳体固有频率随椭圆度的变化

椭圆度是衡量椭圆扁平程度的主要物理参数，同时壳体长度的不同也将影响壳体的固有频率，因此，研究椭圆度及壳体长度对椭圆柱壳固有频率的影响很有必要。图4给出了几种不同壳长比L/mr0下各周向模态阶数n对应的椭圆壳的无量纲固有频率Ω随椭圆度ε的变化曲线。模型参数：ρs=7 800 kg/m3，E=2.1×1011Pa，μ=0.3，h/r0=1/100，壳体两端简支。

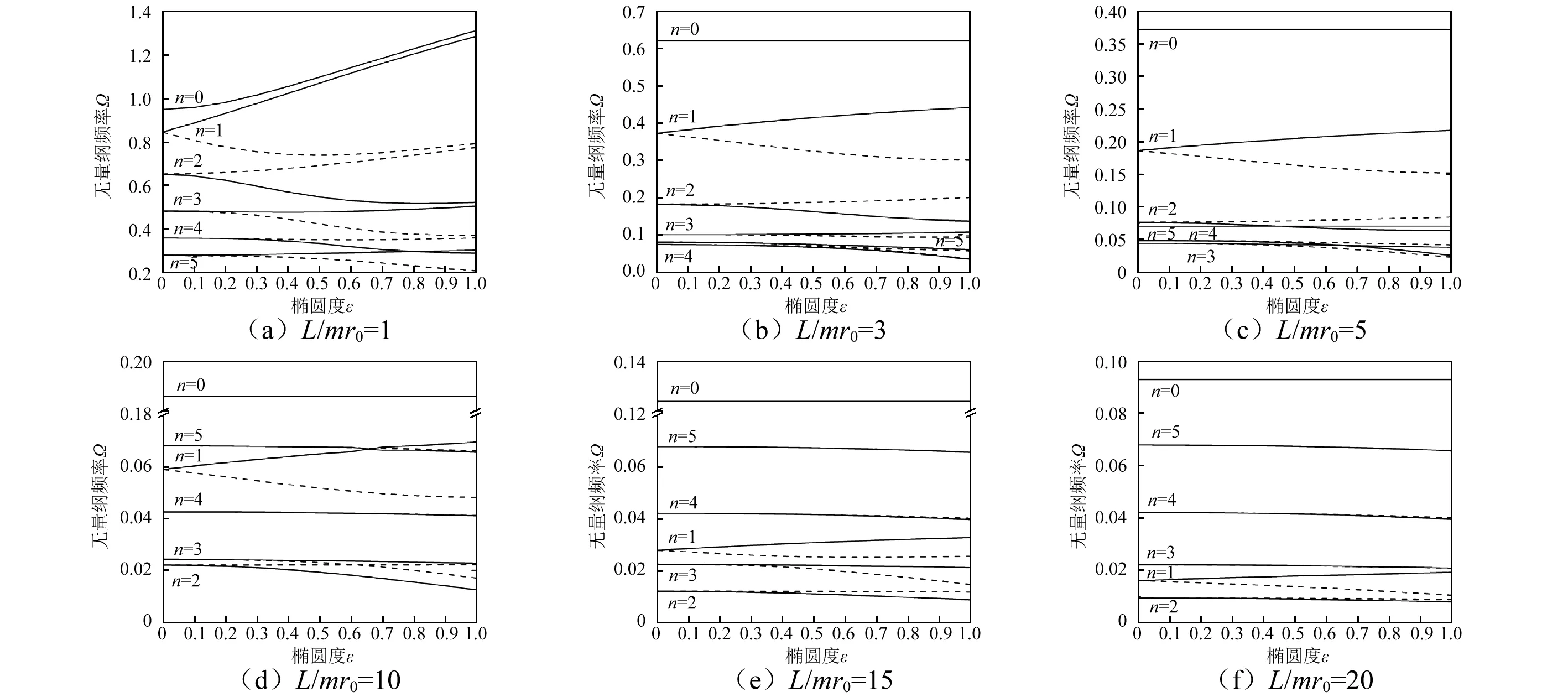
“——”对称模态频率，“……”反对称模态频率图4 固有频率随椭圆度的变化关系 (m=1，两端简支)Fig.4 The relationship between the natural frequency with ellipticity (m=1,simply supported-simply supported)

由图4可知，椭圆柱壳的固有频率相对于圆柱壳有明显的不同，对应于同一周向模态阶数n，椭圆柱壳的对称和反对称模态频率值不相等，两频率的差值随椭圆度的增大而变大。当n=1,3,5等奇数时，椭圆柱壳对称模态频率大于反对称模态频率，当n=2,4等偶数时，反对称模态频率大于对称模态频率，呈现出相反的变化规律。壳体壳长比L/mr0较小时，对应于各周向模态阶数，对称和反对称模态频率均差异较大。当L/mr0较大时，除了n=1以外，其他周向模态阶数对应的对称和反对称模态频率差别不大。当L/mr0=20时，只有n=1对应的对称与反对称模态频率差异比较明显，其它周向模态阶数n对应的对称与反对称模态随频率逐渐趋于重合。

壳长比L/mr0不同，椭圆柱壳基频所对应的周向模态阶数n也不同。当L/mr0>10时，椭圆柱壳的基频对应于周向模态阶数n=2，L/mr0不断减小时，则椭圆柱壳基频对应的周向模态阶数n不断增大。其它周向模态阶数n越接近于基频所对应的周向模态阶数n，则其对应的频率也越低，周向模态阶数n=0所对应的频率一般较高。

在实际工程中，对于柱壳结构，一般都按照理想圆柱壳模型采取减振降噪措施，当存在椭圆度时，壳体固有频率将发生改变。但若能控制壳体的椭圆度，使椭圆柱壳和理想圆柱壳的固有频率差值在一定范围内(如<5%)，则可近似按照理想圆柱壳模型采取减振降噪措施。图5 给出了L/mr0=3和L/mr0=20时，不同周向模态阶数对应的壳体相对频率比值Ωε/Ωc随ε的变化曲线，其中Ωε表示不同椭圆度下椭圆柱壳无量纲固有频率，Ωc表示半径为r0的圆柱壳的无量纲固有频率，即ε=0时的无量纲频率。

从图5可知，不同周向模态阶数n对应的壳体相对频率比值随椭圆度的变化是不同的，壳长比不同时其变化规律也不相同，但若能将壳体椭圆度控制在ε≤0.2的范围内，各周向模态阶数对应的固有频率相对比值差值均<5%，则可以近似将椭圆柱壳视为理想圆柱壳开展减振降噪工作。

图5 壳体相对频率比值随椭圆度的变化(m=1，两端简支)Fig.5 Relative frequency ratio varies with ellipticity (m=1,simply supported-simply supported)

3.4.2 固有频率随壳长比的变化

图6给出了在给定椭圆度ε的情况下，各周向模态阶数n对应的椭圆壳体的固有频率Ω和壳长比L/r0的变化曲线。

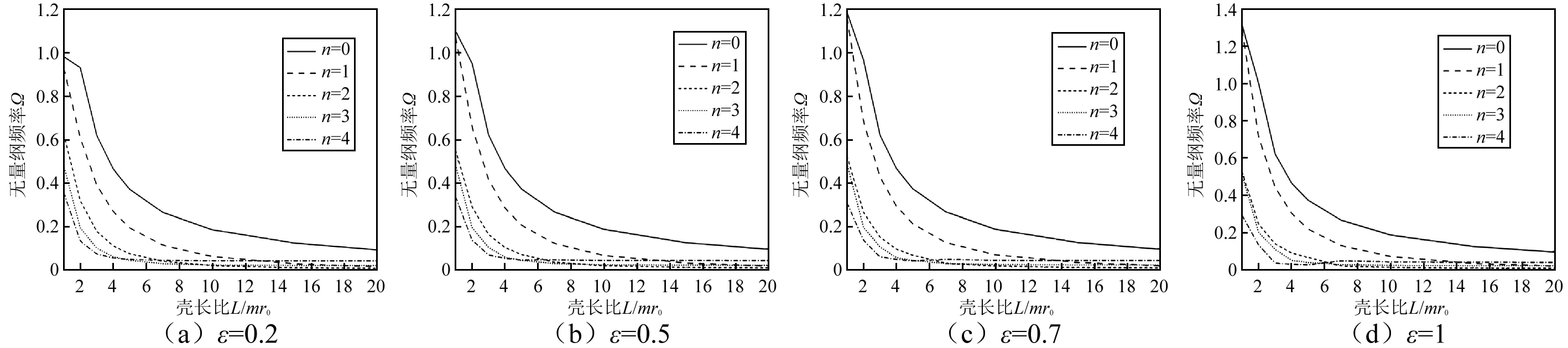
图6 椭圆壳体固有频率和壳长比之间的关系(m=1，两端简支)Fig.6 The relationship between the natural frequency with length ratio (m=1, simply supported-simply supported)

从图6可知：当椭圆度一定时，椭圆柱壳各周向模态阶数n对应的固有频率随壳长比的变化都较为相似，在壳长比较小时，无量纲频率下降较快，当壳长比逐渐增大时，其下降的速率逐渐减小并趋于平缓。表明在给定壳体半径r0以及轴向半波数m情况下，当壳体长度L较短时，壳体固有频率对长度的变化较敏感，长度的改变会引起壳体固有频率的较大变化，但当壳体较长时，壳体长度的改变对结构固有频率的影响较小，与圆柱壳表现出类似的规律。文中只给出了对称模态频率的变化规律，反对称模态与之类似。

4 结 论

本文基于Flügge的薄壳理论推导出真空中椭圆柱壳的自由振动方程，采用波传播法将壳体位移以双Fourier级数形式展开，周向曲率半径以单Fourier级数形式展开，通过级数变换将变系数的偏微分方程组转换为关于周向模态阶数相互耦合的有限阶常系数线性方程组，并由此求解出椭圆柱壳在不同参数下的自振频率，得出如下结论：

(1)椭圆柱壳关于长轴和短轴对称，且对称和反对称模态频率及振型不同。

(2)对应于同一周向模态阶数n，椭圆柱壳的对称和反对称模态频率值不相等，两频率的差值随椭圆度的增大而变大。壳长比较小时，对应于各周向模态阶数，对称和反对称模态频率均差异较大；壳长比较大时，除了n=1以外，其他周向模态阶数对应的对称和反对称模态频率差别不大。

(3)壳体固有频率随着壳体长度的增加而减小，且减小的速率随着壳体长度的增加而降低。

(4)在实际工程中，若能将椭圆度控制在ε≤2.2的范围内，则可以近似将椭圆柱壳视为理想圆柱壳展开减振降噪工作。

[1] 龚有根, 贺玲凤. 含有初始凹陷缺陷圆柱壳稳定承载能力的实验研究与数值计算[J]. 实验力学, 2010, 25(1): 73-80.

GONG Yougen, HE Lingfeng. Experimental study and numerical calculation of stability and load-carrying capacity of cylindrical shell with initial dent[J]. Journal of Experimental Mechanics, 2010, 25(1): 73-80.

[2] 张盛, 金翔, 周桦. 加肋圆柱壳制造误差对声学性能的影响研究[J]. 中国舰船研究, 2011, 6(4): 43-50.

ZHANG Sheng, JIN Xiang, ZHOU Hua. Influence of construction error on sound radiation for ring-stiffened cylindrical shell[J]. Chinese Journal of Ship Research, 2011, 6(4): 43-50.

[3] KLOSNER J M, POHLE F V. Natural frequencies of an infinitely long noncircular cylindrical shell[R]. PIBAL Rept, 476, 1958.

[4] KLOSNER J M. Frequencies of an infinitely long noncircular cylindrical shell[R]. PIBAL Rept. 552, 1959.

[5] CULBERSON L D, BOYD D E. Free vibrations of freely supported oval cylinders[J]. AIAA Journal, 1971, 9(8): 1474-1480.

[6] CARL E K, BOYD D E. Free vibrations of noncircular cylindrical shell segments[J]. AIAA Journal, 1971, 9(2): 239-244.

[7] ELSBERND G F, LEISSA A W. The vibrations of non-circular cylindrical shells with initial stresses[J]. Journal of Sound and Vibration, 1973, 29(3): 309-329.

[8] 朱建雄，曹志远，李国豪. 非圆柱壳在各种边界条件下的自由振动分析[J]. 力学学报. 1992, 24(2): 171-179.

ZHU Jianxiong, CAO Zhiyuan, LI Guohao. Free vibration of noncircular cylindrical shells with arbitrary boundary conditions[J]. Journal of Theoretical and Applied Mechanics, 1992, 24(2): 171-179.

[9] KHALIFA M. Effects of non-uniform Winkler foundation and non-homogeneity on the free vibration of an orthotropic elliptical cylindrical shell[J]. European Journal of Mechanics-A/Solids, 2015, 49: 570-581.

[10] AHMED, KHALIFA M. Simplified equations and solutions for the free vibration of an orthotropic oval cylindrical shell with variable thickness[J]. Mathematical Methods in the Applied Sciences, 2011, 34(14):1789-1800.

[11] 曹雷, 马运义, 黄玉盈. 环肋加强变厚度圆柱壳的自由振动[J]. 华中科技大学学报(城市科学版), 2007, 24(2): 63-66.

CAO Lei, MA Yunyi, HUANG Yuying. Free vibration of ring-stiffened circular cylindrical shell with variable thickness[J]. Journal of Huazhong University of Science and Technology(Urban Science Edition), 2007, 24(2): 63-66.

[12] TORNABENE F, FANTUZZI N, BACCIOCCHI M, et al. Free vibrations of composite oval and elliptic cylinders by the generalized differential quadrature method[J]. Thin-Walled Structures, 2015, 97: 114-129.

[13] NAMAZI M M, AGHANAJAFI C. The analyze of vibration of composite elliptical shell[J]. Australian Journal of Basic and Applied Sciences, 2010(7):1542-1554.

[14] FLÜGGE W. Stress in shells[M]. 2nd ed. Berlin and New York: Spring-Verlag, 1973.

[15] MARGUERRE K. Stability of the cylindrical shells of variable curvature[R]. NASA TM 1302, 1951.

[16] ROMANO F, KEMPNER J. Stresses in short noncircular cylindrical shells under lateral pressure[J]. Journal of Applied Mechanics, 1962, 29(4): 669-674.

[17] ZHANG X M, LIU G R, LAM K Y. Vibration analysis of thin cylindrical shells using wave propagation approach[J]. Journal of Sound and Vibration, 2001, 239(3): 397-403.

Free vibration characteristics of an elliptic cylindrical shell based on the wave propagation method

ZHANG Guanjun, ZHU Xiang, LI Tianyun, MIAO Yuyue

(School of Naval Architecture and Ocean Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)

The free vibration equations of an elliptic cylindrical shell were derived based on the Flügge shell theory. Vibration equations about the circumferential wave number are not decoupled due to the varied circumferential curvature. The shell’s displacements were expanded in double Fourier series in the wave propagation method and the circumferential curvature was expanded in single Fourier series. The partial differential equations with variable coefficients were converted into a set of linear equations which couple with each other about circumferential wave numbers. The natural frequencies of the elliptic cylindrical shell were obtained by solving the coupled equations. The influences of main parameters of the elliptic cylindrical shell, such as ellipticity parameter and shell length ratio, on the vibration characteristics were discussed. The symmetric and anti-symmetric modes of the elliptic cylindrical shell were both considered.

elliptic cylindrical shell; free vibration; natural frequency; ellipticity parameters; anti-symmetric mode

国家自然科学基金(51379083；51479079；51579109)；高等学校博士学科点专项科研基金(20120142110051)

2015-10-27 修改稿收到日期： 2016-04-15

张冠军 男，博士生，1989年生

李天匀 男，博士，教授，1969年生

O327；U663

A

10.13465/j.cnki.jvs.2017.12.031