救援机器人双臂结构设计与运动学分析

王杨俭，陈 炜,2，王立柱，马 利

（1.天津理工大学 天津市先进机电系统设计与智能控制重点实验室，天津 300384；2.军事医学科学院卫生装备研究所，天津 300161）

救援机器人双臂结构设计与运动学分析

王杨俭1，陈 炜1,2，王立柱1，马 利1

（1.天津理工大学 天津市先进机电系统设计与智能控制重点实验室，天津 300384；2.军事医学科学院卫生装备研究所，天津 300161）

基于救灾的复杂环境及实际工作要求，设计了一种新型救援机器人所搭载的双机械臂。利用D-H方法建立双臂的运动学模型，得出双臂末端点的位姿，并求出机械臂的逆解。把三维模型导入ADAMS中得到双机械臂的虚拟样机，对机械臂的虚拟样机工作区域进行求解分析，并通过机械臂模拟实际工作，得出其运动曲线，验证了所建运动学模型的正确性及设计结构的合理性。借助于MATLAB软件采用蒙特卡洛法生成双机械臂工作空间云图及协作空间，为确定机器人的构型、机械臂的长度优化提供了依据，仿真结果表明了机械手臂具备灵活作业的条件，同时为后期的双臂的轨迹规划及控制打下坚实的基础。

双臂救援机器人；运动学；蒙特卡洛法；工作空间云图

0 引言

当前，爆炸、核、生、化、辐射（STHU）泄露或污染以及地震、火灾等自然灾害频发；复杂多变的救灾环境会给救援工作带来更大的困难，灾难发生后搜救幸存者是第一要务，而后灾后现场非结构化环境加上灾后72小时为黄金抢救时间，导致救援人员难以迅速、高效、安全的进行救灾任务。对灾难救援使用救援机器人，不但有效的减少救援工作的时间、危险，并且能够承担人类无法逾越的任务，保障人们的生命和财产安全，减少个人和国家的损失，因此，救援机器人已经成为一个重要的发展方向，具有广阔的应用前景[1～3]。

国内外对救援机器人的研究都取得了丰富的成果。日本东电使用了长约60厘米、高约9.5厘米的棒状机器人进入福岛核电站一号机反应堆安全壳内，获得图像、视频和辐射量等资料，但是由于自身线缆发生了缠绕而影响机器人的移动。BEAR救援机器人由美国维克那机器人公司研制仿人形机器人，它采用的是双履带代替双腿的方法，提高了越障能力，但是结构复杂，双臂协调不足[4]。英国的Weel Barrow型排爆机器人，体积较小，具有一定的灵活性，但其采用的双臂只能通过车体来调整双臂整体抓取方向，限制了机器人在狭小空间中的操作性能[5]。而救援机器人在国内起步较晚，但发展很快。曾参与庐山地震的“小龙虾”双臂机器人在救灾过程中展现了其优越的双臂协调性能，但其体积过大，双臂过于笨重，在复杂的环境中无法开展救援任务[6]。

双臂机器人具有较强的工作能力，能够在恶劣危险的环境下代替人类进行繁琐重复的工作，是当下机器人的研究热点[7,8]。双臂救援机器人主要依靠双臂来完成相应的任务，因此对救援机器人的双臂进行研究尤为重要。本文对救援机器人的双臂结构设计、运动学建模及工作空间的分析展开了研究。首先，基于D-H方法建立了双臂的运动学模型，得出双机械臂末端位姿方程。其次在SolidWorks软件中建立救援机器人的三维模型，并导入ADAMS中，得到机械手臂虚拟样机，然后对机械手臂虚拟样机工作域进行求解分析。最后基于蒙特卡洛数学分析方法得出双臂运动工作空间及双臂协调工作范围，并对双臂的工作空间进行分析，为以后双机械臂协调及轨迹跟踪打下坚实的基础。

1 机械手机构设计

履带式机器人的总体结构由履带式车体、车体的摆臂以及双机械臂构成，机器人车体上搭载各种传感器、视频模块、动力模块、控制模块和电源模块。双臂的位置位于履带式车体的前部。图1为履带式救援机器人的整体示意图。

在SolidWorks建立双臂三维模型，图2为双臂三维模型。双臂中每个单臂结构为三个关节四个自由度度机械手+手爪组成的机械臂，三个关节分别为回转关节、肩关节及肘关节，四个自由度分别为腰部的回转、肩部转动的俯仰、肘部的转动到俯仰和末端手爪的开合，可以使手爪在空间内达到任何位置。末端负载为5kg～10kg。图3为机械臂的机构简图。

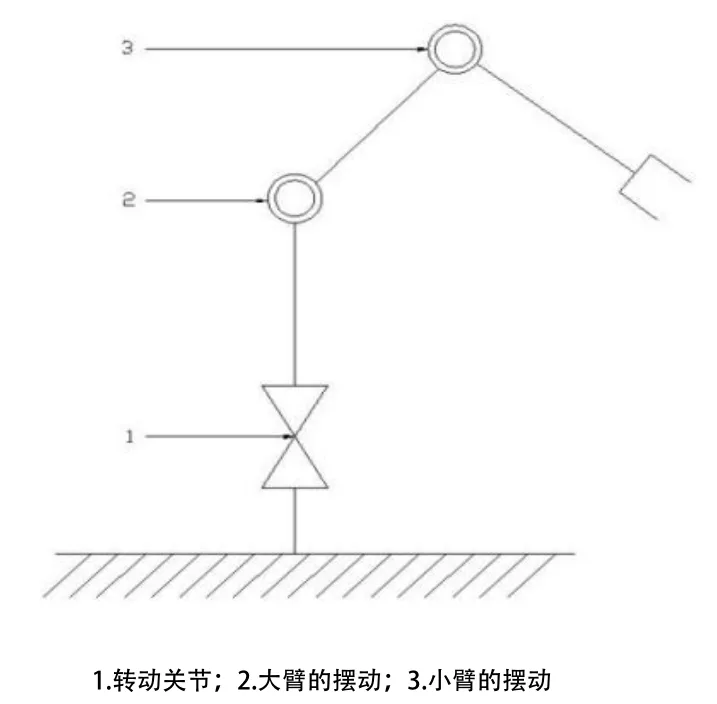
图3 机械臂机构简图

手爪结构如图4所示，为了使机械手爪的结构更加紧凑，抓取物体更加灵活，手爪设计了一个自由度，即手爪的张合。手爪张合是由电机带动锅杆，锅杆带动两侧涡轮，两侧涡轮的转动方向相反，涡轮带动上下钳口，从而实现物体的抓取。并在上下钳口处配有一些橡胶材料，能够进一步提升与待处理对象的摩擦力，手爪在抓取物体时不易滑落。

机械臂关节模块属于支撑大臂小臂回转模块，其在调整末端执机构所处的位置有不可或缺的作用。

承载能力、自锁能力和成本是机械臂考虑的主要因素。基于以上要求本文在设计机械手的关节时，采用的是涡轮蜗杆的传动方式，一方面能够准确实现自锁，另一方面涡轮蜗杆有较大的传动比，便于机械臂的运动控制。故在机械臂的转动关节采用涡轮蜗杆的传动机构。如图5所示为手臂的转动关节。

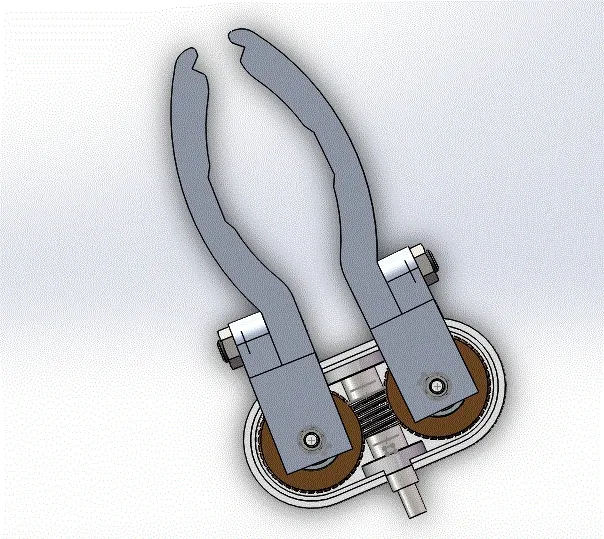
图4 转动关节

图5 转动关节

2 双臂运动学分析

双机械臂运动学就是建立在各运动构件与末端执行器（即手爪）的空间姿态之间的关系，为系统控制提供分析的手段和方法。基于上述结构建立双臂的各关节分布如图6所示。

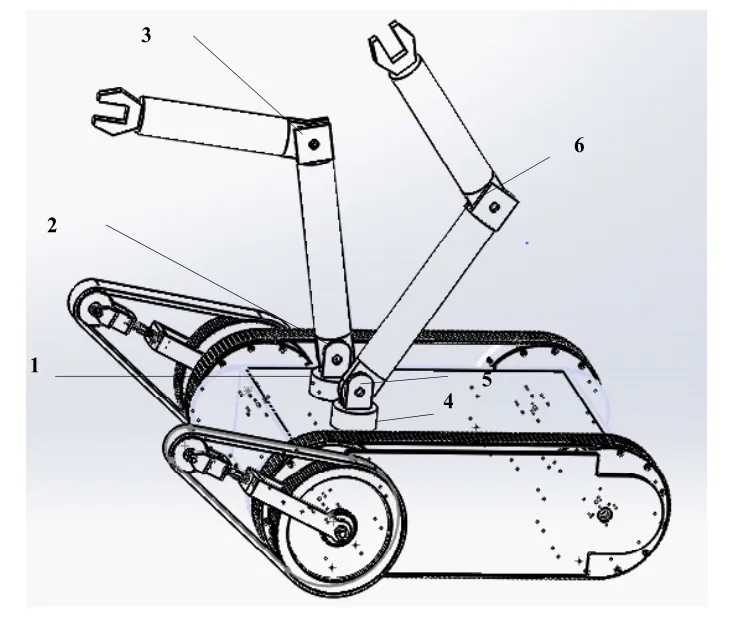
图6 机械手关节及连杆

2.1 坐标系建立

人口数量与区域生产能力的关联度分析——以清至民国陕北黄土高原为例……………………………………王 晗（182）

在运动学求解中以车体为基础坐标系（X0，Y0，Z0），采用D-H方法建立坐标系，在每个连杆的末端建立端点坐标系，最终建立双臂连杆坐标系如图7所示。表1给出了各关节的运动参数。

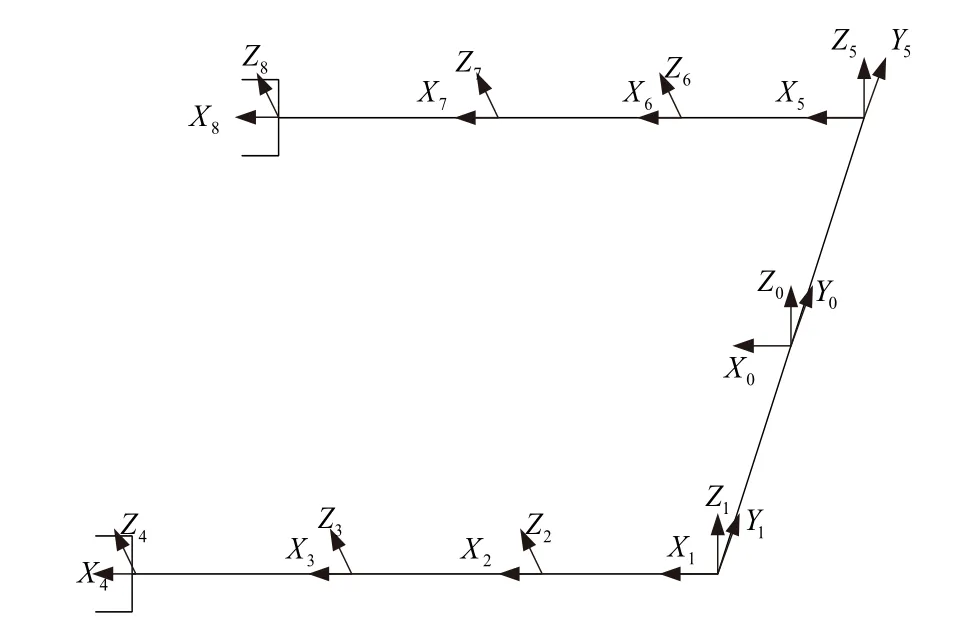
图7 双机械臂的坐标系

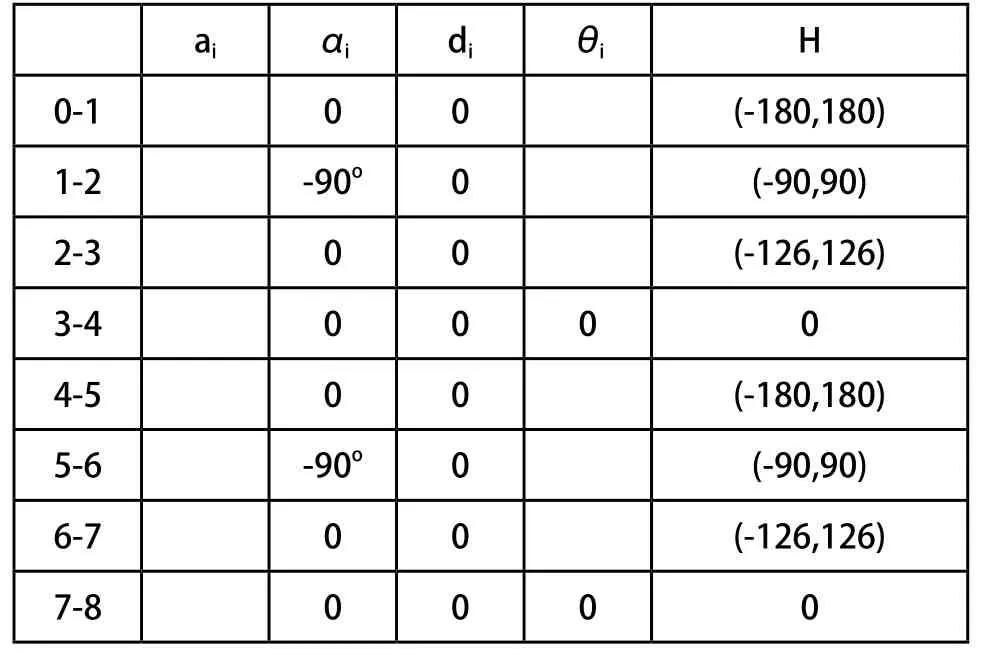
表1 机器人D-H参数表

连杆坐标系{i}相对于{i-1}的变换 称为连杆变换。可以将 分解为 ， ， ， 四个基本自变换，将连杆变换 可以看做坐标系{i}经过变换得到：

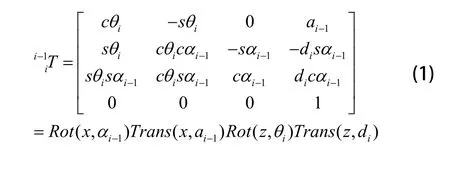
设机械手臂末端点的姿态 表示。

2.2 机械手的正运动学

机器人手臂的正运动学问题是已知机器人手臂关节角度求出末端执行器的位姿。将各连杆的变换矩阵按着从左到右的顺序依次相乘得到相对于基坐标机械手末端点的其次变换矩阵。现以左臂为例，将表1中的参数带入式(1)中求出左机械臂每个连杆的变化矩阵：

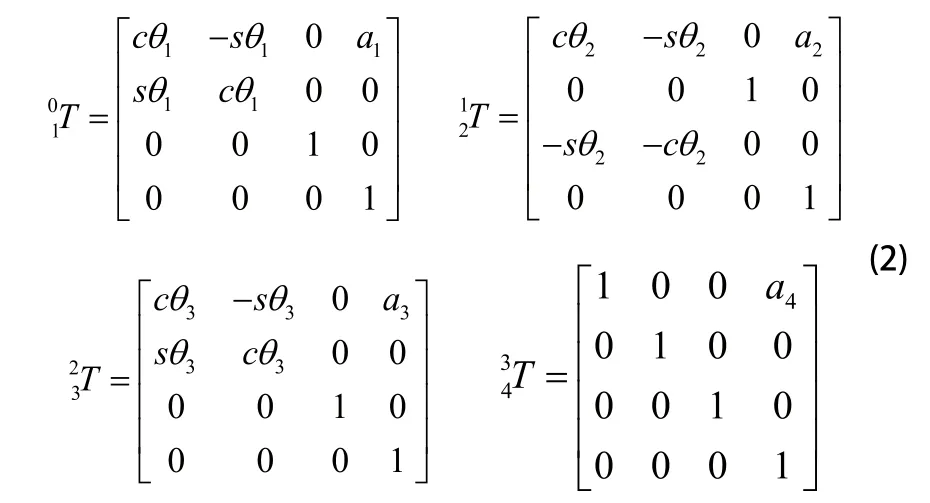
求出机械手末端姿态 =P。

在P的各元素为：

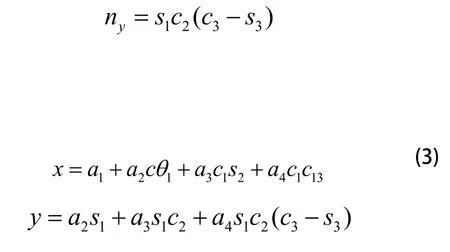
式中ci为为分别为1至3。

2.3 机械手臂的逆解

在单一的串联机械手中，其自由度小于或等于6时可解，因此本文中双机械臂运动学是可解的。双机械臂的结构关于基坐标系的XOY面对称，其逆解的求解过程及结果近乎相同，以双机械臂的左臂为例求解。由于有很多角度的耦合，所以用矩阵的逆左乘，各元素对应相等，已知末端执行器的情况下，求出相应角度的解如下：

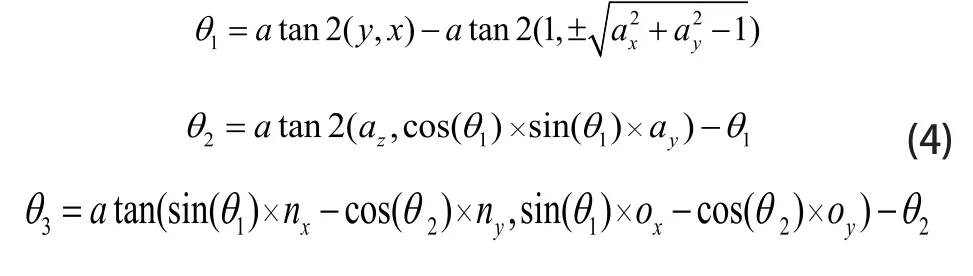
3 虚拟样机的建立

利用ADAMS虚拟仿真对手臂进行相关的测试，能够及时快速的查找问题、解决问题，避免手臂在制造之后出现不必要的问题[9]。

履带式救援机器人由履带式底盘和两个机械手构成。两个机械手臂分布在救援机器人的两侧，并相互配合工作。机械臂模型在不影响结果前提下进行适当的简化，如图8所示为简化流程图。

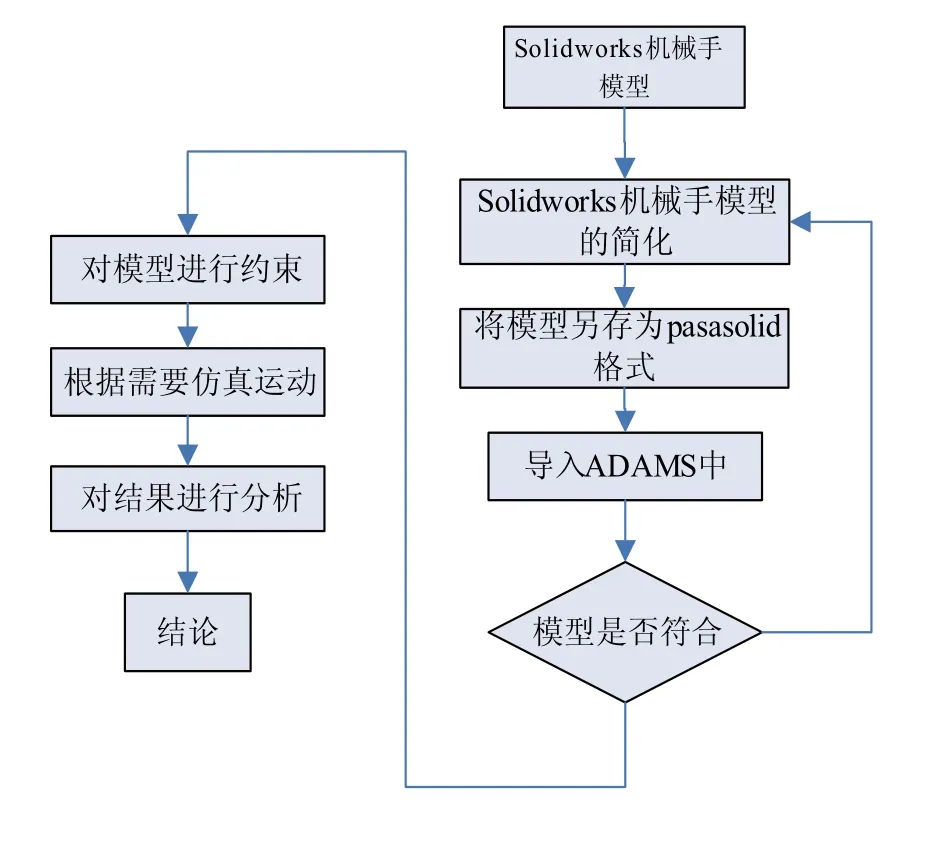
图8 流程图

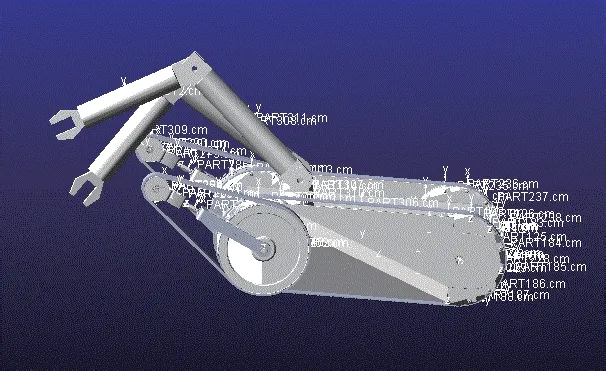
图9 导入ADAMS中的三维模型

将救援机器人模型导入ADAMS中，如图9所示，导入后对各个零件进行重命名，设置相应的材料属性，赋予质量后，对机械臂相应的零件添加关节限制，并对每个关节施加相应的驱动函数，完成相应的动作分析，得出机械臂运动曲线。

以其中一个机械臂的ADAMS虚拟样机输出的曲线为例，根据机械手参数和基本设计指标对虚拟样机中一个臂进行仿真可以得出工作区域及机械手臂任意点的轨迹。

在机械手的肩关节、肘关节加电机驱动，运动方式选择转动，再输入各关节的驱动函数，如下：

肩关节：step（time，6，0d，10，160）+step（time，20，0d，25，-180d）

肘关节： step（time，6，0d，10，120）+step（time，20，0d，25，-120d）

在机械手的仿真过程中，使机械臂腰关节及手爪处于锁紧状态，进而使机械手自由度为零。对机械手爪的mark点进行轨迹绘制从而得出机械手在平面内运动理论工作域如图10所示。

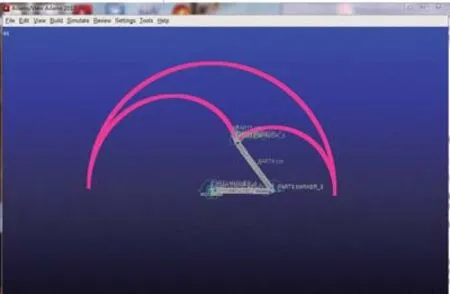
图10 机械手运动的理论的工作域

在仿真完成后，进入ADAMS/POSTPROSS对手爪位置标记点进行x和y方向进行位置测量，得到位置仿真曲线图，如图11所示。

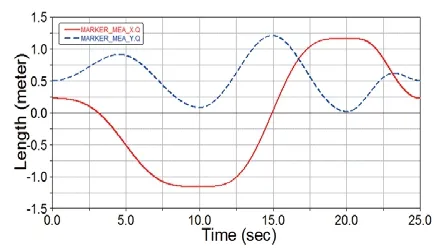
图11 机械手臂的x、y位置仿真曲线

通过手臂的ADAMS运动学仿真可以对前面的建立的方程进行验证及分析。在设计阶段对机械手的关节赋予相应的驱动函数，模拟手臂在实际运动控制中的特定的动作，分析手臂的运动情况。

取双臂机械手的左臂进行ADAMS运动仿真。对机械手的肩关节、肘关节施加相应的驱动函数。因为手爪的爪取和腰关节的转动与其他关节之间存在较少联合运动，所以对驱动函数赋予0。在手爪的上标记mark点，并测试该点在x，y方向的位移及相应关节所转的角度，输出测量值，运动仿真如图12所示。

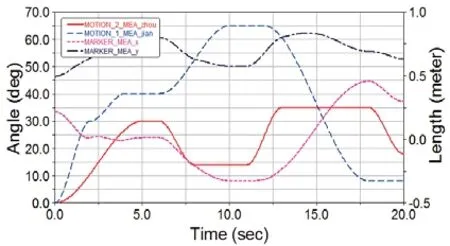
图12 机械手爪标记点x，y位置及相应关节角度θ之间的关系

如图12所示MOTION_2_MEA_zhou为肘关节对应时刻所转的角度，MOTION_2_MEA_jian为肩关节对应时刻所转的角度，MARKER_MEA_x为手爪标记点marker在x方向的运动的坐标，MARKER_MEA_y为手爪标记点marker在y方向的运动的坐标，则（x，y）为相对于机械手腰关节的坐标，所以可以将关节角度曲线和机械手的位移曲线结合在一起进行分析，可以得到角度和位移的关系。从图12中取任意时刻的对应的角度带入第三节中左臂的正运动方程中得出标记点的坐标值，将仿真结果和所计算坐标值相互验证可以对所建立的运动学方程正性。将图12中9s中对应的转角MOTION_2_ MEA_jian=64,MOTION_2_MEA_zhou=12带入机械手正运动方程中得到x方向位移为-0.3168，y方向位移为0.5735，仿真的结果为x=-0.3168，y=0.5735，验证了建立的运动学的正确性。

4 工作空间的计算

蒙特卡洛法是借助随机抽样来解决数学问题的方法，蒙特卡洛法借助于MATLAB软件计算出机器人的工作空间。本文根据每个关节取相应的转动范围，当每个关节随机的取得转角时，带入双臂末端点位置方程中得出末端点的位置，在MATLAB中编写相应程序，生成双臂的工作空间云图[10]。

蒙特卡罗法求解步骤如下：

1）求解出双臂履带式救援机器人的其中一个臂的正解，并算出其末端位置左右手臂末端的位置（x，y，z）。

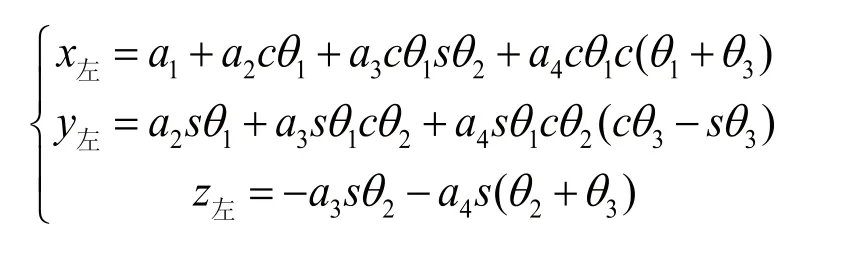
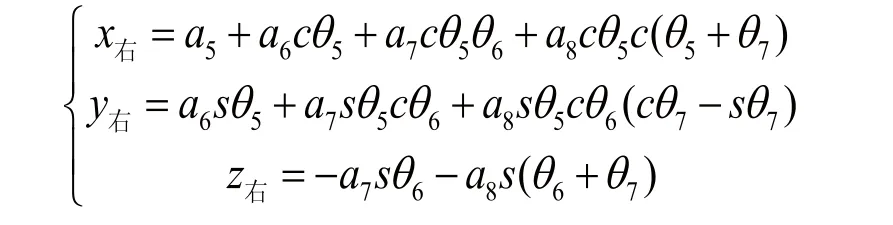
2）在MATLAB中应用Rand对各个转角产生随机值，其公式为

3）带入机械臂的正解中，生成N个位置坐标。

4）将位置坐标在MATLAB中生成图像。

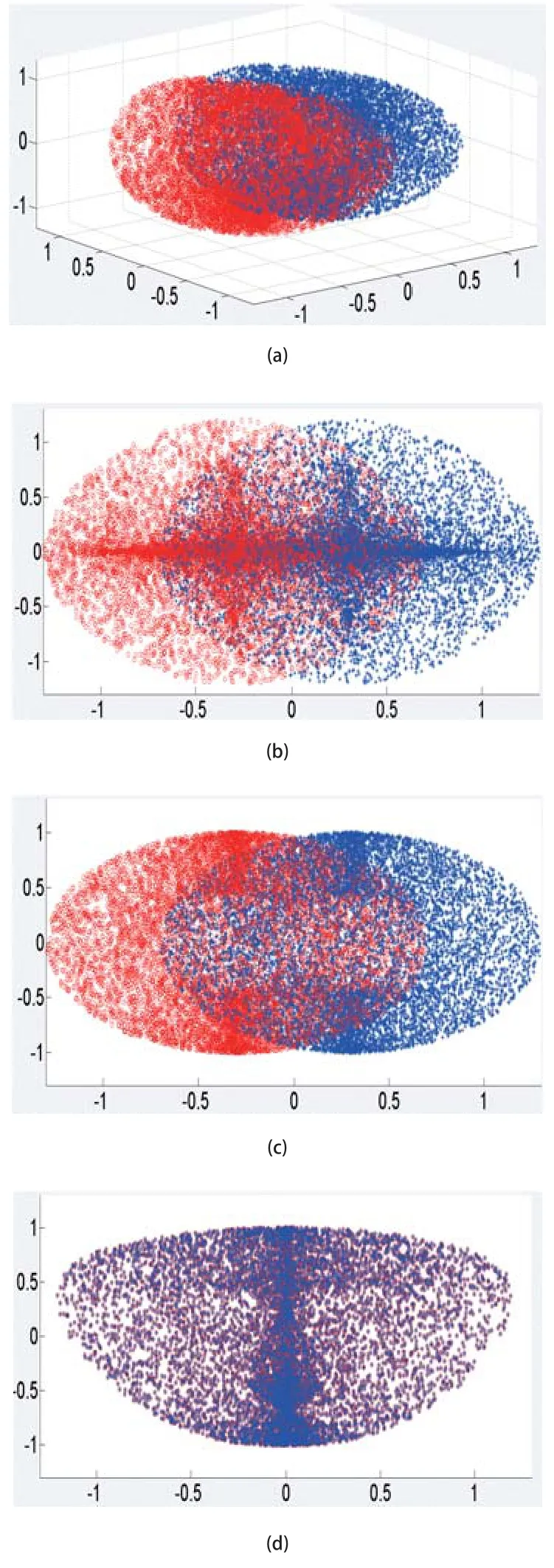
图13 双臂的工作空间云图

【】【】

得出以上机械手双臂的工作空间云图，图13是双臂空间三维视图，图中(a)、(b)、(c)、(d)分别为XYZ三维空间图、XOY、XOZ、YOZ视图，通过以上仿真结果可知，图像中没有明显的空洞，履带式机器人机械臂的机构紧凑，得出两个机械手末端点的运动范围，双臂的左臂在X方向运动范围为（-0.689，1.288），Y方向运动范围（-1.187，1.212），Z轴方向涌动范围（-0.878，0.999），双臂中右臂X方向运动范围为（-0.989，0.999），Y方向运动范围（-1.187，1.212），Z轴方向涌动范围（-0.878，0.999），所以双臂总的运动范围为：X轴方向（-0.989，1.298）Y方向运动范围（-1.197，1.202），Z轴方向涌动范围（-0.878，0.999），而且能够得出双臂相互重叠的区域为双臂协调工作的区域，该区域所占总区域比较大，能够满足双臂协调曲抓取物体的要求。同时为双臂的轨迹规划及协调做好坚实的基础。

5 结论

本文根据救援机器人工作时面临复杂环境及救灾任务设计了新型双机械臂结构，分别对机械臂的手爪及转动关节进行设计，在机械臂的传动关节处采用蜗轮蜗杆传动；并对双机械臂利用D-H法建立运动学方程得到两个机械臂末端位置的姿态并求出逆解，同时利用ADAMS将SolidWorks三维机械手臂的模型进行虚拟模型的仿真，得到机械手臂的理论工作区域，给定机械手关节驱动函数完成特定的动作，得出运动曲线，验证建立运动学的正确性；根据机械臂的末端姿态，结合蒙特卡洛法和MATLAB计算出双臂机器人的工作空间云图，通过分析其具有足够的协调空间，并为后续双机械臂的轨迹跟踪和协调控制做好基础工作。

[1] 刘亢,尚红.地震救援机器人在芦山7.0级地震中的应用[J].减灾技术与方法消防技术与产品信息,2013,(5)：26-28.

[2] 郭月,等.救援机器人的研究现状与发展趋势[J].医疗卫生装备, 2014,35(8)：22-26.

[3] BowdenM.Black Hawk Down,A story of moder war[M].New Yowk：arone Press.2010;32-33.

[4] 苏卫华,吴航,张西正,等.救援机器人研究起源、发展历程与问题[J].军事医学,2014,38(11)：981-985.

[5] Okada Y,NagataniKJ,YoshidaK,etal.Shared autonomy system for tracked vehicles on rough terrain based on continuous three_dimensinal terrain scaning[J].Journal of Field Robotics,2011,28(6)：875-893.

[6] 张涛,等.机器人技术在地震废墟搜索救援中的应用[J].自然灾害学报,2012,21(5),108-112.

[7] 寇彦芸,万褶,赵修林,等.地震救援双臂机器人结构设计与运动分析[J].机械设计与制造,2016,(10)：142-146.

[8] Wong K.Dual arm robot.US.Parent D646,703[P].2011-10-11.

[9] 吴硕,吴桐,赵继忠.多自由度机械臂运动控制系统的设计与仿真[J].制造业自动化,2017,36(10)：108-111.

[10] 翼宾松,郝敬宾,王飞龙,等.折叠双臂式机器人运动学与工作空间分析[J].科学技术与工程,2016,16(25)：91-97.

Structure design and kinematic analysis of dual arm robot

WANG Yang-jian1, CHEN Wei1,2, WANG Li-zhu1, MA Li1

TP242.3

：A

：1009-0134(2017)05-0089-06

2017-03-13

国家自然科学基金（11302147）

王杨俭（1990 -），男，山东德州人，硕士，研究方向为机械电子工程。