燃气涡轮发动机滑模参数限制调节系统设计分析

张园锁，陶金伟，黄 浏，张 哲，谢瑾瑜

（中国航发商用航空发动机有限责任公司，上海 200241）

燃气涡轮发动机滑模参数限制调节系统设计分析

张园锁，陶金伟，黄 浏，张 哲，谢瑾瑜

（中国航发商用航空发动机有限责任公司，上海 200241）

设计了一种基于滑模控制的参数限制调节系统，能够对燃气涡轮发动机的燃油流量进行调节确保其在全转速范围内工作时候工作关键运行参数限制内。首先，基于滑模控制原理开展了滑模调节系统的结构设计，该调节系统主要由主滑模调节器、限制参数滑模调节器和高低选选择器组成；其次，基于通用的非线性涡轮发动机模型开展了模型辨识，获取了在调节器设计点的线性模型；然后，基于线性模型证明了所设计的滑模调节系统的渐近稳定性；最后，基于混合2-范数和无穷范数为优化目标获取了反馈增益，并通过初步调试获取了满足过渡态时域控制指标的滑模控制参数（边界层厚度、切换增益）。基于如上设计的调节系统结果仿真表明：1）滑模非线性调节系统能够保证涡轮发动机在全转速内的稳态和过渡态控制品质；2）所设计的滑模调节系统中参数限制调节器能够在发动机过渡态过程中一直起作用，克服了线性调节传统中参数限制调节器不能在过渡态过程中实施限制作用的弊端；3）采用滑模边界层厚度参数可以抑制和消除滑模控制过程的控制量的“抖振”现象。

滑模；辨识；参数限制；调节系统；设计

0 引言

作为高复杂性航空动力系统，燃气涡轮发动机部件众多、机理复杂，而其核心机（主要包括压气机、燃烧室和涡轮三大部件）则以工作环境条件极其恶劣（高温、高压和高转速）一向是发动机设计的重点，核心机的稳定运行直接决定了涡扇发动机的各种性能指标和安全性指标是否达到；同时，燃气涡轮发动机以其工作转速范围内高度的非线性对控制设计提出了很大的挑战；如何设计出既能对运行关键参数（高压压气机、燃烧室和高压涡轮的气动热力参数等）进行限制保护同时又能够兼顾稳态推力及功率指标、动态加速响应的控制系统，一直是当前动力装置控制研究领域的前沿问题[1～4]。

参数限制及保护不仅关乎发动机的安全运行，良好的参数限制更使得发动机压气机喘振裕度提升和熄火倾向减小，从而延长了发动机的寿命[5]。本文针对涡扇发动机核心机关键参数的限制保护设计了一种调节系统进行了初步的设计和方针分析研究，此调节系统基于变结构的滑动模型控制方法[6]。

滑模控制方法主要采用矩阵理论和微分几何数学工具，滑模调节器的设计可避免针对被控对象的传递函数开展耗时的频域整形迭代设计；且由于滑模控制以李亚普诺夫稳定性定义为理论基础，可针对非线性的被控对象直接开展调节器的设计，无需将被对象分段线性化后逐段设计线性调节器[7]。鉴于滑模控制此诸多的优点，其已在工程领域被大量实践和应用，如飞机防滑刹车系统滑移率控制[8]，车辆跟车控制[9,10]，卫星机动控制[11]，导弹制导控制[12]，永磁同步电机控制[13]，城市轨交地铁停车控制[14]，内燃机气门升程控制[15]，混合动力汽车自适应巡航控制[16]等。在滑模方法航空发动机控制应用方面，国内空军工程大学的苗卓广等人在模型预测滑模控制[17]、粒子群优化网络整定航空发动机全程滑模型控制[18]等方面开展了较为全面的探索和研究，国外的Hanz Richter在文献[19]中也对滑模控制在航空发动机控制方面的应用进行了较为深入的论述和实践。

本文所设计的滑模参数限制调节系统主要由滑模调节器、选择器和积分器三大部分组成，作为调节系统核心的滑模型调节器为非线性调节器，相比传统的基于“增益调度”的线性调节器为核心部件组成的线性参数限制调节系统，新的调节系统从理论层面克服了过渡态过程限制保护的不足，确保了在有限时间内达到限制值，且避免了不同调节器之间不停切换导致的不稳定现象。虽然滑模型控制方法有如上诸多优点，但由于滑模控制本质上是一种非线性控制，其不可避免地会引入控制的不连续性，即常见的滑模调节器输出的控制量“抖振”的现象，本文中也针对滑模调节器非线性的特点，对非线性进行了近似处理，在一定程度上抑制了滑模非线性调节器固有的“抖振”，同时达到了对被控对象关键运行参数限制的目的。

1 滑模调节系统设计

通用的燃气涡轮发动机参数限制保护调节器调节目标将发动机从任意初始稳态点控制到另一个稳定的目标稳态点两个稳态点之间的过渡控制过程中，如果被限制参量未达到其限制值则发动机转速可达到，若控制过程触及被限变量，则发动机状态则稳定在此限制值。传统线性调节器通过各个被控或被限变量形成的单输入单输出（SISO）回路计算的控制指令进行高低选来实现，高低选逻辑的复杂性导致其稳定性不能保证，过渡态时被限制参数经常出现超限，限制回路提前抢占主控回路控制权等现象，导致实际的参数限制管理功能、性能达不到指标要求[5]。

1.1 滑模调节系统结构设计

本文设计了一种滑模参数限制非线性调节系统，本调节系统主要由非线性调节器[20]（主滑模调节器、滑模限制调节器）、选择器、积分器和线性被控对象模型组成，系统架构如图1所示。

滑模参数限制调节系统的具体设计过程如下。

1.1.1 对象模型设计

本文研究的被控对象为单轴的燃气涡轮发动机，其主控制输入为燃油流量（Wf），主被控输出为轴转速N1，被限制参数为压气机出口静压和总温（P3、T3）、涡轮排气总温（EGT）；选择N1为状态量，在发动机模型某稳态点附近区域，可用如下简化的线性状态空间模型来近似描述。

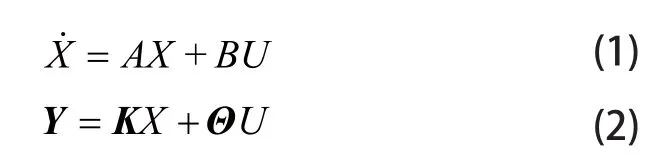
式(1)、式(2)中X=ΔN2为调节系统受控对象模型的状态变量， 为调节系统受控对象模型的输入变量，为调节系统受控对象模型输出，K为4×1维调节系统受控对象状态输出矩阵，Θ为4×1维调节系统受控对象输入输出矩阵。

滑模调节系统的设计需要基于被控对象的稳态特性工作线，本文所设计的调节系统的被控对象为通用的燃气涡轮发动机非线性模型，且满足如下的非线性离散数学关系式。

图1 滑模参数限制调节系统控制架构

对发动机的燃油输入Wf作小阶跃扰动则控制量Wf满足下式。

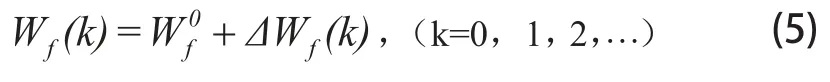
状态量N2(k)和输出量Y(k)的序列值均由(3)获取为已知，根据最小二乘拟合思想，直接建立如式(6)的最小二乘问题模型。

由(6)所获取的 既可以保证子在稳态点附近待拟合线性系统符合最小二乘意义下的最小化。由式(3)、式(5)、式(6)获取式(4)系数过程，鉴于各变量原始数值（式(3)驱动下状态变量和输出变量序列数值）之间相差数个数量级，可以基于稳态点数值对方程(4)中离散变量进行归一化，在此不再赘述此归一化过程的数学变换，详细的非线性模型辨识线性模型的方法可参阅文献[21]。

基于如上小阶跃方法的线性化辨识结果式(7)慢车附近状态起始点系数矩阵，式(8)最大推力附近状态起始点系数矩阵。

1.1.2 积分器设计

本文设计调节系统为保证被控或被限变量无稳态误差，对被控对象输入使用了积分环节，引入式(9)中间变量Ur，即为待设计的调节器输出。

1.1.3 调节器设计

针对如式(1,2)描述的发动机模型，设计如下滑模量：

系统达到滑模态时满足如下方程：

根据李亚普诺夫第二方法[22,23]，若能够找到一个标量李亚普诺夫函数，使函数满足三个李亚普诺夫条件：1）李亚普诺夫函数正定；2）李亚普诺夫函数的导数负定；3）且当函数变量趋近无穷时，李雅普诺夫函数亦趋近于无穷，则可以判定说设计的系统全局渐收敛于平衡状态点。本文基于如上定义的滑模量，选择的李亚普诺夫函数如下[20,22]。

容易知道，下式子成立。

图2 滑模参数限制调节系统主滑模调节器控制原理

图3 滑模参数限制调节系统限制滑模调节器控制原理

即，李亚普诺夫的在平衡状态点时为零，其他状态大于零；且随着状态量远离平衡点趋向于无穷远时候李亚普诺夫函数亦趋近于无穷。

为保证在有限时间内系统从任意初始平衡状态达到滑模稳定状态，下面的李亚普诺夫导数条件式子必须成立。

为满足式(16)要求，选取等速指数衰减的趋近律[19,20]，只需要式(17)成立即可：

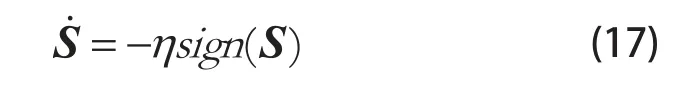
式(17)中η为某一恒定正数，其反映了滑模变量S收敛于目标滑模面稳态点切换运动特性的常数，即切换增益系数，假设系统从初始点经由时间tr到达滑模态，即S(tr)=0，对式(17)进行积分，结果如式(18)所示。

考虑如式(17)滑模量运行满足指数衰减趋近规律，要求系统运动达到稳态滑模面过程中滑模量S符号不变（保证系统在滑模运动过程单调趋近零的特性），因此式(18)可转换为式(19)。

联立式(1)、式(2)、式(10)、式(11)、式(17)可得式(20)成立，写成分量形。

考虑上面式(17)中连续的滑模变量Si会有无限多次通过零点，对Si进行数值积分不可行，式(20)且获取的控制量具有跳跃性质，实际工程控制的作动机构无法完成此种跳变执行任务，且即使在仿真环境也对数值积分结算器的很大挑战。鉴于符号函数的引入会对滑模运动过程产生“抖振”的控制现象[24,25]，本文采用如下的饱和函数近似代替符号函数来描述滑模变量Si的渐近趋近特性[19,20]，并同时抑制滑模运动的抖振现象，符号函数的处理如式(21)所示。

上式中正常数φ反映滑变量切换的边界，简称为边界层厚度。

1.1.4 选择器设计

设计低选-高选选择律为：

式(22)中，L={1，2，…，l}且H={1，2，…，h}，Urzj是与低选选择器相联接的滑模参数限制调节器输出，Urzk为高选选择器相联接的滑模参数限制调节器输出，主滑模调节器输出直接默认连接在低选器上，其输出为Ur1。

基于文献中论证限制保护的不变性特性选取器关联准则[20,26]，可将不同的调节器输出Ur分配到相应的选择器上面,保证所设计调节系统的参数限制功能，具体设计的高低选设计结果如表1和图4所示。

表1 滑模调节器低选-高选选择器设计结果

图4 滑模控制量高低选调节器原理图

1.2 滑模调节系统参数设计

本节主要对本文设计的滑模参数限制调节系统中由式(2)描述的输出变量系数矩阵进行求解。本文设计的滑模参数限制调节系统的中被控对象可简化为单输入多输出（SIMO）模型，输入变量为Wf，输出变量为N2、压气机出口温度T3和静压P33、排气温度EGT，且被控输出变量设计点随着发动机初始稳态推力状态不同而改变。

参数限制变量（T3，EGT和Ps3）的Ki和Θi（i=2，3，4）由初始系统稳态点对应的被控对象线性状态空间模型对应的输出矩阵确定，且Θ1也通过线性状态空间模型确定。

本部分基于状态反馈控制律对滑模调节系统中被控对象控制量U=Wf进行了设计[27,28]，即如式(23)所示。

描述调节系统在滑模控制起始稳态点附近的线性模型状态方程如式(1)和性能输出方程如式(24)、(25)所示。

将式(23)代入式(2)、式(24)、式(25)可获取式(26)、式(27)、式(28)所示：

分别对式(26)、式(27)、式(28)进行拉氏变换并联立的式(29)、式(30)。

其中GU,Z2为发动机模型输入U到性能输出Z2的传递函数；GU,Z∞为发动机模型输入U到性能输出Z∞的传递函数。

本文采用带有混合H2/H∞范数优化的区域极点配置方法对参数K进行寻优设计，采用2-范数和无穷范数加权表示优化目标，即采用式(31)设计目标，寻求使被控对象输Wf到输出（T3、EGT和Ps3）混合范数M最小的反馈增益K。

上式中，a和b是非负的权重值，本设计中a=0.5和b=0.5，表明H2和HH∞优化目标的权重相同。

本文设计的滑模调节系统反馈增益K以发动机地面慢车附近状态点和最大推力附近状态点的线性模型为基准，设计结果表示如式(32)所示，式中为主滑模输入调节系数。

对状态变量N2的反馈控制律的反馈增益矩阵K的设计过程进行了说明，滑模控制参数限制管理调节器的可调参数为Φ和η，此两变量用于对算例仿真过程滑模量响应进行调整确定[20]。

1.3 滑模调节系统稳定性设计

本部分主要对滑模参数限制调节系统架构的稳定性进行初步的证明，证明本文设计的系统在全局渐近稳定，同时保证在有限时间内达到限制值而不超限。

工程上常用的发动机线性调节系统稳定性设计基于李亚普诺夫第一方法[23,29,30]，即如果非线性被控模型微偏线性化后，获取的线性系统特征多项式全部极点均在左半平面，则可判定原来非线性系统是稳定的。本文设计的调节系统基于李亚普诺夫第二方法，如利用前面式(13)表示的李亚普诺夫函数，可知，李亚普诺夫第二法要求的两个条件已经满足，仅需保证式(17)成立即可证明所设计的滑模参数限制调节系统稳定。

式(17)的详细的论证过程此文不做直接证明，具体细节可参考文献[20]，本文直接引用此篇文献中的定理12，若保证下面三个条件成立，即可保证本文设计的滑模参数限制调节系统是全局渐近稳定。

A为非奇异矩阵；

式(20)控制输入经由式(22)选择律选择后，式(1)和式(2)表示的被控对象运行轨迹在有限的时间内渐近收敛于唯一的平衡点X。

在GI1和MTO两个起始稳态点，由式(7)、式(8)、式(32)数据验证，上面两个条件均满足，即本文设计的滑模参数限制调节系统全局渐近稳定。

2 仿真试验及分析

2.1 滑模调节器建模说明

本部分主要基于本文2.2节滑模参数限制调节器设计原理进行了建模，其主要包括主滑模调节器设计建模、限制保护滑模调节器设计建模、滑模控制量低选-高选选择器设计建模和调节器综合建模等，具体结果如下：

基于图2主滑模调节器控制原理，本文设计的主滑模调节器如图5所示。

由图3受限输出滑模调节器控制原理，设计受限变量（EGT示例）滑模调节器如图6所示。

由滑模主调节器、滑模受限输出调节器、低选-高选选择器、积分器和控制对象组成的调节系统动态仿真模型如图7所示。

2.2 滑模调节器仿真及分析

本文采用通用涡扇发动机核心机的实时非线性模型，分别采用如上所设计的滑模非线性参数限制调节系统和传统的增益可调线性参数限制调节系统对模型进行了控制仿真。

仿真环境采用5ms定步长模型，仿真模型主要基于如上所设计的滑模参数限制调节系统和非线性发动机模型，组成包括非线性滑模调节器（主滑模调节器、参数限制滑模调节器）、高-低选选择器、滑模控制量积分器、非线性发动机模型和指令模块组成，详细结构如图8所示。其中发动机模型输入接口被封装为单燃油流量输入简化模型，输出包括N2（核心机转速）、T3（高压压气机出口总温）、EGT（高压涡轮出口总温）和Ps3（高压压气机出口静压）。

本文模拟了发动机从GI1（地面慢车）附近推力状态到MTO（最大起飞）附近推力状态，然后再回到GI2附近推力状态的参数限制管理仿真试验。

图5 主滑模调节器仿真框图

图6 受限输出滑模调节器仿真框图

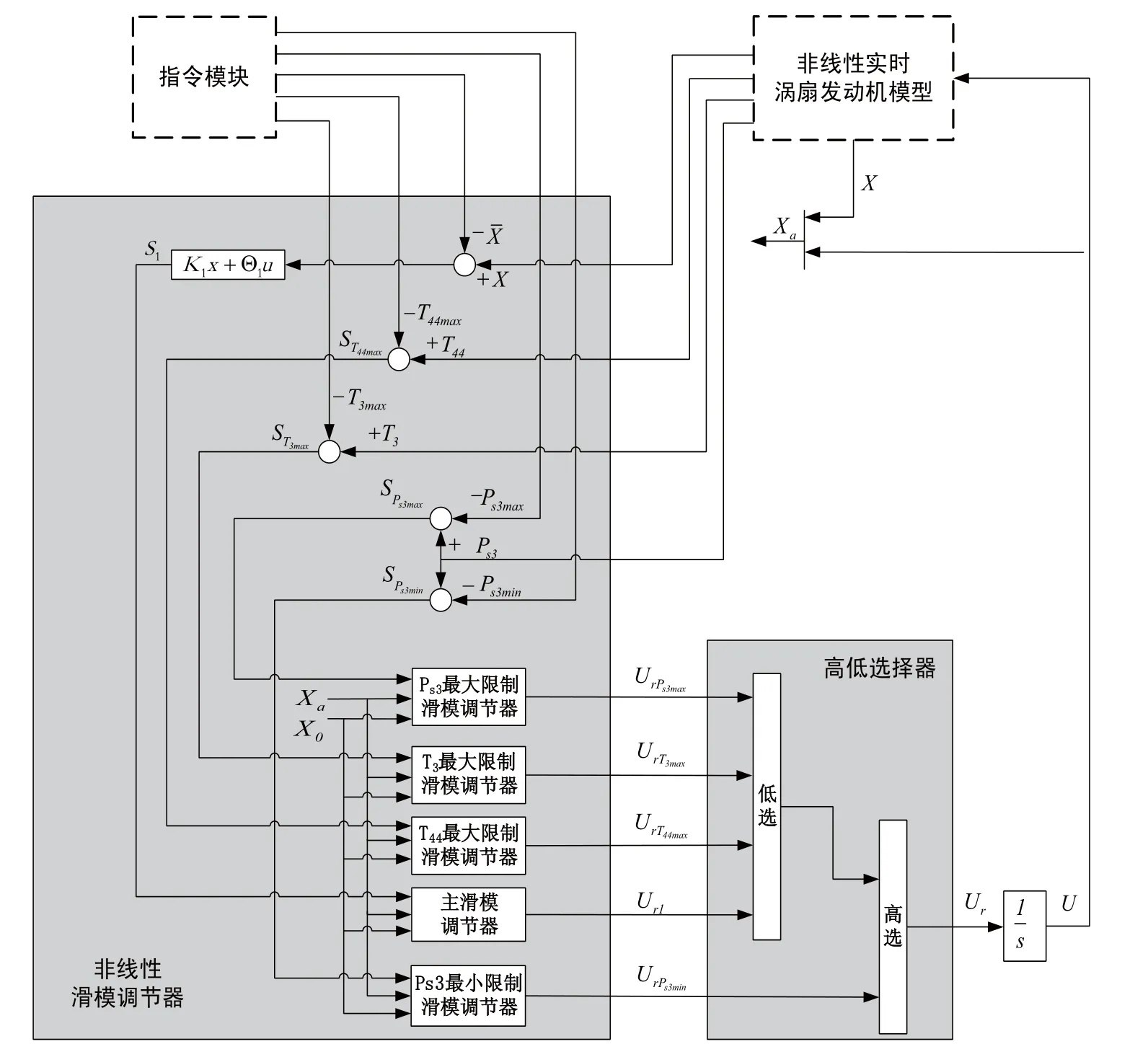
图7 滑模参数限制动态调节系统控制原理图

图8 滑模参数限制动态调节系统仿真框图

仿真的发动机模型设置为地面静止标准海平面条件：高度H=0m，马赫数Ma=0且标准温差DT=0。常规燃气涡轮发动机从地面慢车推力至最大推力再返回值地面慢车过程，均需要将发动机设计成不仅达到推力和功率指标（N2目标值为衡量推力和功率是否达到的标准）而且此过程不会超出各参数的设计限制值，本发动机及其模型运行同样满足这种要求。因此，考虑到演示参数限制的目的，本数字仿真试验下调设置最大Ps3限制值为Ps3max=2000kPa、最大T3限制值为T3max=1000K、最大EGT限制值为EGTmax=1350K和最小Ps3限制值为Ps3min=1200kPa。

下面是仿真试验结果的分析过程，其中图12和图13中的状态参数响应采用归一化模式，相关的参数定义为：T3_r=T3/T3max，Ps3_r=Ps3/Ps3max，EGT_r=EGT/EGTmax，N2_r=N2/N2,D（其中，N2,D为本仿真发动机设计点转速）。

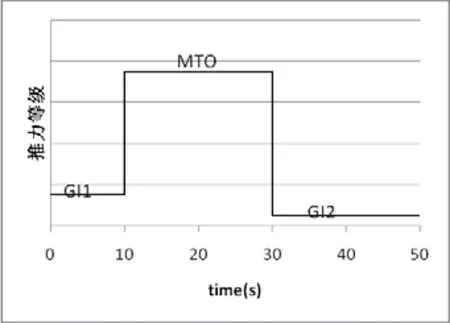
图9 滑模控制参数限制管理仿真测试用例

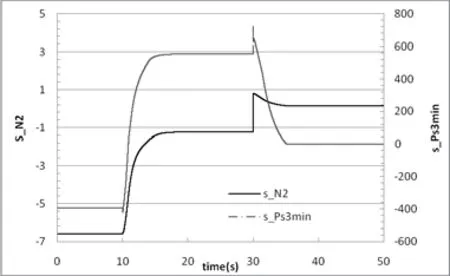
图10 N2主控回路和Ps3最小值限制回路滑函数变化

图11 T3、EGT和Ps3最大值限制回路滑变量变化

图12 滑模控制参数限制动态调节系统的参数（归一化）响应

由图10，图11滑函数的变化曲线可知，本文设计的滑模型调节器（包括主滑模调节器、参数限制滑模调节器）在对发动机进行控制过程无明显的“抖振”想象，由滑模量计算得出的燃油控制量可以直接作为燃油计量机构的期望并有伺服控制器执行实时的闭环控制任务。

综合图10，图11，图12仿真结果可知：在加速过程，加速开始5s左右，相对T3和EGT最大限制值，Ps3最大限制值最先达到（Ps3_r=1）且Ps3最大值参数限制调节器的滑变量s_Ps3max同时达到0，即加速过程达到S_ Ps3max=0滑模稳定状态；T3和EGT最大值限制回路未达到限制值，其滑函数s_T3max和s_EGTmax分别从S_ T3max(0)=-289.6及S_EGTmax(0)=-414.0向值为0的方向移动，加速过程结束时仍未到达各自的滑模态。在减速过程，减速开始5s左右S_Ps3min=0达到0，即Ps3最小值限制回路达到（Ps3_r= Ps3min/ Ps3man=0.6），即减速过程达到s_Ps3min=0的滑模稳定状态。

图13 线性调节器参数限制动态调节系统的参数（归一化）响应

图13为基于增益调度的线性调节器参数限制动态调节系统仿真响应，与图12滑模控制参数限制动态调节系统相同的测试用例。

由图13可知，在从慢车状态至最大起飞推力状态的加速过程中，线性调节器前期控制效果较为“陡”后期较过于“缓慢”，导致整体加速调整的时间较慢达到8s左右，这和EGT最大值线性调节器过早抢占加速调节器并由其主控整个加速调节过程有直接关系，而线性限制调节器的调节时间通常较主控调节器长；滑模调节器的加速调整时间约5s左右，且滑模过程EGT滑模调节器受限突破零值，迅速回调后较快地过阻尼单调趋近零值S_ EGT=0，达到滑模稳定状态，即由EGT限制值确定的发动机稳定状态。

在从最大起飞状态至慢车状态的减速过程中，同样，线性调节器前期控制效果较为“陡”后期较过于“缓慢”，导致整体加速调整的时间较慢达到7s左右，这和Ps3最小值线性调节器过早抢占减速调节器并由其主控整个减速调节过程有直接关系，而线性参数限制调节器的调节时间通常较主控调节器长；滑模调节器的减速调整时间约5s左右，且滑模过程Ps3滑模调节器受限突破零值后轻微超调，迅速回调后很快地过阻尼单调趋近零值S_Ps3min=0，达到滑模稳定状态，即由EGT限制值确定的发动机稳定状态。

3 结束语

由本文的数字仿真试验可知，相对传统的基于参数自适应调度的线性调节器，滑模控制在航空发动机上的应用具有如下五个方面的优点：

1）滑模控制调节系统得的设计过程不需要分段线性化，只需根据发动机的稳态特性图（滑模起始点状态空间模型）即可设计；

2）控制参数的设计采用区域极点配置的混合H2/ Hinf综合范数优化算法，滑模调节器参数对被控模型参数变化的具有较强的鲁棒性，且确保了在大范围过渡态控制过程，以混合过程控制指标最小化准则保证了整个控制过渡过程品质；

3）滑模控制在主控回路和受限回路的控制指令高低选原则清晰，且滑模调节器可保证所设计系统的全局渐近稳定性，相比传统线性调节器中对各回路计算的控制量进行解耦选择的复杂逻辑特性，大大降低了调节系统内部逻辑设计的复杂度而又不损失调节系统的各种性能指标；

4）过渡态度无需设计相应的控制器，过渡态主要有滑模参数限制调节器完成，克服了传统线性调节系统中线性参数限制调节器在发动机过渡态过程无法起作用的弊端[4,19]；

5）滑模调节器参数的设计过程直接对标时域指标，通过调整η和Φ可分别对控制过程调节时间和调节器输出“抖振”进行调校，相比根轨迹图解法、频响法、状态空间法[27,28,30,31]设计调节参数能极大缩短迭代调试工作量。

鉴于滑模控制方法具有全局渐近稳定性、过渡控制性能品质最优化、参数限制保护功能良好、调节器器设计调试简单等方面的优点，后续进一步优化本文所设计的滑模调节系统的架构，融入随发动机状态和飞行环境条件变换的线性发动机模型，开展全飞行包线范围内的滑模参数限制调节仿真；另外，逐步开展离散时间滑模调节器设计，并尝试通过发动机电子控制器（EEC）验证设计的离散滑模算法[32]，尝试与线性调节器综合后验证，逐步提升滑模控制在燃气涡轮发动机推力控制和参数限制中的成熟度及应用价值。

[1] 樊思齐.航空发动机控制[M].西北工业大学出版社,2008.

[2] 姚华.航空发动机全权限数字电子控制系统[M].航空工业出版社,2014.

[3] 孙建国,黄金泉,等.现代航空动力装置控制[M].航空工业出版社,2009.

[4] 黄开明,尹泽勇,黄金泉.参数限制对涡轴发动机过渡态控制的影响[J].航空动力学报,2006,21(2)：432-436.

[5] Link C. Jaw, Jack D. Mattingly, Aircraft engine controls design, System Analysis, and Health Monitoring[M].Virginia (USA)：AIAA,2009.

[6] 刘金琨,孙富春.滑模变结构控制理论及其算法研究与进展[J].控制理论与应用,2007,24(3)：407-418.

[7] 李殿璞.非线性控制系统理论基础(第二版)[M].北京：清华大学出版社,2014.

[8] 付龙飞,田广来,王鹏,等.飞机防滑刹车系统滑移率自适应滑模控制研究[J].西北工业大学学报,2015,33(5)：770-774.

[9] 施继忠,张继业,徐晓惠,胡永举.随机干扰的车辆跟随系统滑模控制[J].西南交通大学学报,2015,50(6)：1088-1093.

[10] Shengbo Eben Li, Kun Deng, Keqing Li. Terminal sliding control of automated car following system without reliance on longitudinal acceleration information[J].Mechatronics,2015,30(9)：327-337.

[11] 常琳,孙金光,范国伟,徐开.基于terminal滑模控制的小卫星机动方法[J].光学精密工程,2015,23(2)：485-496.

[12] 齐辉,张泽,韩鹏鑫,等.基于反演滑模控制的导弹制导控制一体化设计[J].系统工程与电子技术,2016,38(3)：618-623.

[13] 王志宏,王翔,吴益飞,等.基于特征模型的PMSM调速系统离散自适应滑模控制[J].南京理工大学学报,2015,39(6)：637-642.

[14] 王青元,吴鹏,冯晓云,张彦栋.基于自适应终端滑模控制的城轨列车精确停车算法[J].铁道学报,2016,38(2)：56-63.

[15] Mohammad Pournazeri,Amir Khajepour. Precise lift control in a new variable valve actuation system using discrete-time sliding mode control[J].Mechanism and Machine Theory,99.217-235(2016).

[16] Behnam Ganji,Abbas Z.kouzani, SuiYang Khoo. Adaptive cruise control of a HEV using sliding mode control[J].Expert system with applications,2014,41(2)：607-615.

[17] 苗卓广,谢寿生,王磊,等.航空发动机多模型预测滑模控制[J].推进技术,2012,33(3).

[18] 苗卓广,谢寿生,何秀然,等.自适应PSO网络整定的航空发动机全程滑模控制[J].推进技术,2011,32(3).

[19] Hanz Richter.Advanced Control of Turbofan Engines[M]. Springer. USA.2011.

[20] H.Richter. A multi-regulator sliding mode control strategy for output-constrained systems[J].Automatica 47.2251-2259(2011).

[21] 陆军,郭迎清,陈小磊.线性拟合法建立航空发动机状态变量模型[J].航空动力学报,2011,26(5)：1172-1177.

[22] Michael S. Branicky, Multiple Lyapunov Functions and Other Analysis Tools for Switched and Hybrid Systems[J].IEEE TRANSACTIONS ON AUTOMATIC CONTROL,1998,43(3)：475-482.

[23] 吴麒,王诗宓,杜继宏,等.自动控制原理[M].2版.清华大学出版社,2006.

[24] Kang Hongbo, Shen Yu.On limit cycle chattering in sliding mode control systems under the influence of sampling intervals based on describing function approach[J].The Journal of China Universities of Posts and Telecommunications,2016,22(1)：55-59.

[25] Yuanyuan Zhang, Renfu Li, Tao Xue, Zhimin Liu, Zongxin Yao, An analysis of the stability and chattering reduction of highorder sliding mode tracking control for a hypersonic vehicle[J]. Information Sciences,2016,348(1)：25-48.

[26] F. Blanchini, Set invariance in control[J].Automatica,1998,35：1747-1767.

[27] Gene F.Franklin, J.David Powell, Abbas Emami-Naeini.自动控制原理与设计[M].6版.电子工业出版社,2014.

[28] R.Dorf, R. Bishop.现代控制系统[M].12版.电子工业出版社,2013.

[29] H.K. Khalil. Nonlinear Systems (Third Edition) [M].USA：Prentice-Hall Inc.,2002.

[30] 胡寿松.自动控制原理[M].6版.科学出版社,2013.

[31] Karl Johan Astrom, T. Hagglund, PID controllers： theory,design and tuning[M].Pennsylvania(USA)：Instrument Society of America,1995.

[32] Gene F.Franklin, J.David Powell, Michael Workman. Digital Control of Dynamic Systems(Third Edtion)[M].USA：Addison-Wesley,1998.

Design and analysis of parameter limit regulating system based on sliding mode control in gas turbine engine

ZHANG Yuan-suo, TAO Jin-wei, HUANG Liu, ZHANG Zhe, XIE Jin-yu

V233.7

：A

：1009-0134(2017)05-0022-09

2016-11-01

张园锁（1983 -），男，河南人，硕士，研究方向为航空燃气涡轮发动机控制系统工程设计、控制理论及算法的工程应用的设计与验证、控制系统软件设计与验证。