解题中应加强学生的模型辨别
——从一道函数模型问题谈起
筅山东省邹城市第二中学陈玉伟
解题中应加强学生的模型辨别
——从一道函数模型问题谈起
筅山东省邹城市第二中学陈玉伟
高中数学解题千千万,然而若能培养学生模型辨别,则可以解决众多类似问题.例如,高中数学许多问题围绕函数展开.对于同一个函数问题,我们可以有一些相近意思的理解,因此可确定不同的函数模型进行研究,但是由于函数模型结构的差异、参量个数的不同,对于后续研究的难易程度会天差地别.笔者以一道函数问题为例,谈谈这类问题的一般步骤.
一、题目呈现
设函数f(x)=lnx-ax,g(x)=ex-ax,其中a为实数.
(1)若f(x)在(1,+∞)上是单调减函数,且g(x)在(1,+∞)上有最小值,求a的取值范围;(2)若g(x)在(-1,+∞)上是单调增函数,试求f(x)的零点个数,并证明你的结论.
二、解法分析
解:(1)略(2)当a≤0时,g(x)必为单调增函数
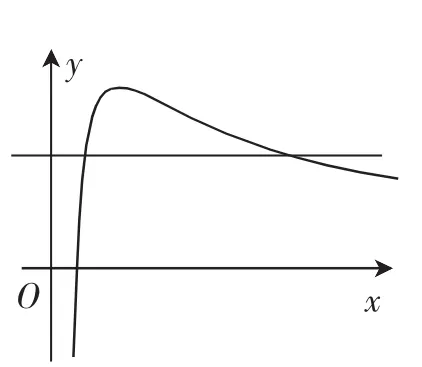
当a>0时,令g′(x)=ex-a>0,解得a
∵g(x)在(-1,+∞)上单调增函数,∴lna≤-1即0 ②当a<0时f(ea)=a-aea=a(1-ea)<0,f(-1)=-a>0,且函数f(x)在[ea,1]上图像不间断∴f(x)在(ea,1)上存在零点.另外,当x>0时,f′(x)=-a>0,故(fx)在(0,+∞)单调增函数,∴f(x)只有一个零点. ③0 当0 ∴x=a-1是f(x)的最大值,且最大值为f(a-1)=-lna-1 (i)当-lna-1=0,a=e-1时,f(x)有一个零点 (ii)当-lna-1>0,0 本题为典型研究函数单调性求函数值域问题,笔者进行研究归纳出高中阶段研究函数三步骤仅供大家参考.(确定函数:确定函数解析式及定义域(研究函数:研究函数性质及图像(解决问题:根据性质解决函数问题.学生学习完导数之后对于给定不含参量的函数解析式均能研究,因此三步骤中最关键的应是第一步:确定函数. 因此笔者根据以几种不同相近的理解,确定几种相近解析式,通过比较难易程度进行归纳选取何种解析式较好.因此题(2)还可以有其他解法: 方法2:将f(x)=0变形,lnx-ax=0圯lnx=ax, ①确定函数:确定函数解析式及定义域: 同时研究y1=lnx,y2=ax两个函数定义域为(0,+∞) ②研究函数:研究函数性质及图像: 两个函数两个函数单调性均较为简单,因此我们借助图像研究 图1 (1)a≤0时,由图像可知两曲线只有一个交点(图1) (2)a>0时,由图像可知两曲线可能有一个交点(图2)可能两个交点(图3),临界情况为相切,因此先算出相切时a的值. 图2 图3 ③解决问题:根据性质解决函数问题 综上所述:当a≤0或a=e-1时,f(x)的零点个数为1, 当0 方法3:法2中同时根据lnx-ax=0圯lnx=ax,同时研究y1=lnx,y2=ax 笔者在此基础上进行变形lnx-ax=0圯lnx=ax圯a= 同时研究y1=a ①确定函数:确定函数解析式及定义域: ②研究函数:研究函数性质及图像: ③解决问题:根据性质解决函数问题根据图4可知: 当a≤0或a=e-1时,f(x)的零点个数为1,当0 反思:三种方法均为本题探究零点问题的理解,但是后续研究问题的复杂程度,难易程度差距很大.方法1直接研究f(x)本身,方法2通过变形进行转化研究两个较为简单的函数,方法3在方法2的基础上进一步简化为一个常数函数与一个不含参量的函数(俗称参变分离)大大减少运算量.因此我们应尽量利用参变构造出这两类函数简化运算. 图4 (2)设g(x)=x2-2bx+4.当a=时,若对任意x1∈(0, 2),存在x2∈[1,2],使 f(x1)≥g(x2),求实数b的取值范围 在研究函数问题时第一步确定函数往往决定了整题研究的难易程度.按照参变分离确定一个常数函数与一个不含参量的函数进行研究函数问题可以避免讨论参数与区间关系进而大大减少运算量. 波利亚认为,解题后反思是有效解题的一个重要而有益的阶段,反思整个解题过程,并再次思考、核实结果及获得结果的方法,从而掌握数学知识,并培养数学解题能力.对于同一个函数问题,可确定不同的函数模型进行研究,但是由于函数模型结构的差异、参量个数的不同,对于后续研究的难易程度会天差地别.研究函数三步骤中第一步非常关键,我们遇到含参量问题时,应尽量确定一个常数函数与一个不含参量的函数进行简化,这样往往有意想不到的简化效果. 教师要引导学生学会解题后反思:这道题主要考查了哪些知识点?最优解法是哪种?对于相同的题型,要归纳通法通解,对于不同的题型要熟知解题策略.在平时的教学中,教师要先行深度剖析这类问题,才能从容归纳问题的普遍性与特殊性,才能有效地指导学生解题后反思.学生需要反思:几个变式主要涉及到哪些知识点?解法之间有怎样的联系?一些解法的本质是什么?诸多解法中最优解法是哪个?能否归纳通法通解?解决最值问题的一般方法有哪些?通过解题后反思,学生再次面对最值问题时不再雾里看花般触摸不到,并让他们体悟归纳具体题型的解题方法,养成勤于探究、及时反思的好习惯.三、模型提炼方法引申



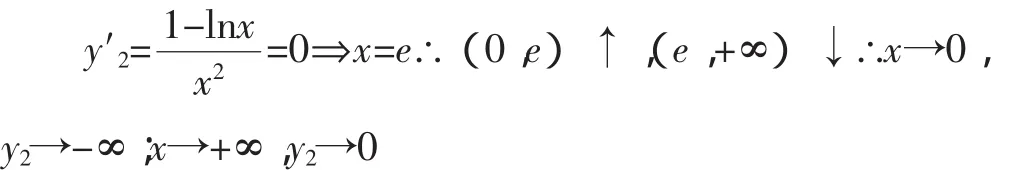
四、链接试题,巩固提升
五、思想提炼反思提升

