浅谈教材的再开发

筅安徽省临泉第一中学熊文文

浅谈教材的再开发

筅安徽省临泉第一中学熊文文

教材为教师教学的基本工具，是学校教育的核心资源，是实施教学活动的主要材料.但由于编者限制于教材的篇幅和知识的深度，对很多问题无法完全展开和延伸，这就需要教师发挥个人智慧，根据教学实际情景对教材进行适当的补充、拓展，是教材更适合学生的学情，更有利于学生对知识的掌握，有利于学生的思维发展和技能培养.

笔者下面就略谈一下自己对教材再开发的一点感受，以期抛砖引玉.

一、从概念出发，挖掘概念，开发概念

概念教学中的重点问题是我们的概念教学往往只是念课本，缺乏必要的挖掘、延伸.

案例1椭圆的概念教学时，第二定义出现的非常突兀，如何让学生更好地接受第二定义呢.在第一定义的教学时，求椭圆的标准方程，化简|MF1|=|MF2|，代入可，即动点到顶点的距离与它到定直线的距离的比为一个常数，即圆锥曲线的第二定义.第二定义的推出，自然而然，学生很容易接受.

二、从定理、公式出发，开发教材

课本中的一些定理，由于篇幅或者难度限制，没有证明或者延伸，教师可以根据学情和教学的实际情况，进行补充或延伸.

案例2公式的证明.

案例3定理、公式的应用.

空间向量的基本定理，在平时的教学中，我们很少关注它，只是把它当做引入空间直角坐标系的铺垫.殊不知，看着没用的知识点，用起来是那么顺手.所以，平常教学，要注意定理的开发、应用.

①应将发展基层水利作为政府解决“三农”问题的关键性措施。只有发展好基层水利，才能确保农业增产、农民增收和农村发展，才能搞好社会主义新农村建设，从根本上解决好“三农”问题。

图1

例1（2013年全国卷理19题）如图1，四棱锥P-ABCD中，∠ABC＝∠BAD＝90°，BC＝2AD，△PAB和△PAD都是等边三角形.证明：PB⊥CD.

证明：PA=PB=PD，∠BPA=APD=60°，∠BPD=90°.以

这种解法，即可帮助学生理解定理、掌握定理，又可锻炼学生的思维能力，开阔视野.

三、从教材例题、习题出发，挖掘例题、习题

案例4从例题的解题出发，通过一题多解、一题多变帮助学生理解掌握知识，拓展视野、思维.

例2（北师大版数学教材必修4第二章第五节例2）在△ABC中，设边BC，CA，AB的长度分别为a，b，c，证明：a2=b2+c2-2bccosA，b2=c2+a2-2cacosB，c2=a2+b2-2abcosC.

证法一：利用向量证明.

图2

图3

证法二：解析法.

如图3，在△ABC中，设边BC，CA，AB的长度分别为a，b，c，点A与原点重合，点B的坐标为（ccosA，csinA），由两点间的距离公式可得，a2=|BC|2=（ccosA-b）2+（csinA）2=b2+［（ccosA）2+（csinA）2］-2bccosA=b2+c2-2bccosA.

同理可证其他两个公式.

证法三：转化化归法，把任意三角形转化为锐角三角形.

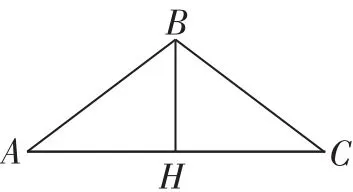
图4

图5

证明a2=b2+c2-2bccosA.

（1）当A=90°时，显然成立.

（2）当0°

（3）当90°

设AB=c，BC=a，AC=b，AH= ccos（180°-A）=-ccosA，BH=csin（180°-A）=csinA，CH=bccosA，在直角三角形BCH中，BC2=BH2+CH2，a2=（bccosA）2+（csinA）2，化简得a2=b2+c2-2bccosA.所以在△ABC中，有a2=b2+c2-2bccosA，同理可证其他两个公式.

例3（北师大版数学必修1第57页第11题）某同学为授助失学儿童，每月将自己的零用钱以相等的数额存入储蓄盒，准备凑够200元时一并寄出.储蓄盒原有60元，两个月后盒内有90元.写出盒内钱数（元）与存钱月数的函数解析式.

分析：当函数定义域为x∈R，没有实际意义了，那函数的解析式又是什么？

得到解析式：

对于这个习题的开发，笔者还是很自豪的.通过探索，找规律，猜想得到了解析式，虽然不是很严密，但是对刚进高一的学生已经很了不起了，学生甚至发现了周期，体验了学习的快乐，成功的喜悦.通过对一道习题的挖掘，提高了学生学习数学的兴趣，培养了学生动手能力及探索能力，收获巨大.

四、从教材的探究材料出发，让学生参与数学，体验数学

北师大版教材高中数学必修4第一章末正方体的截面的形状探究.让学生动手探究，体验数学，感受数学，培养空间想象力，得到如下结果.（1）用一平面截正方体，当平面经过正方体的三个面时，所得的截面的形状为三角形.（2）截面是四边形.用一个平面截正方体，当平面经过正方体的四个面时，所得截面可能是正方形、长方形、梯形.（3）截面是五边形.（4）截面是六边形.2013年安徽卷就考查了正方体截面问题，学生很吃力而这个探究问题在书本上早就出现了，一直没有引起教师、学生的注意而已.

当然，教材的开发是多样的，也可以从课本中的留白出发，从信息技术与数学图形、方程求解等出发，也可以从课本中的思考交流、抽象概括出发，也可以从教材的阅读材料、数学史出发等.而且教材的再开发也是仁者见仁智者见智，可以发挥教师和学生的智慧.无论怎么样，都是从学生出发，从学情出发，从课堂教学出发，从教材出发，对教材适当的再加工，使它更适合当时的教学，教师要下足功夫，开发教材，这样才能避免题海战术，才能为学生减负，才能更有利于学生的学习、成长.当然，开发教材对教师是一件辛苦的事，但结果会令人欣慰，付出是值得的.F