立足本质促进对话,深度发展提升智慧
——由一节二轮复习课引发的思考
筅安徽省灵璧第一中学郑良
立足本质促进对话,深度发展提升智慧
——由一节二轮复习课引发的思考
筅安徽省灵璧第一中学郑良
高三二轮复习如火如荼,结对的年轻教师C(第一次带毕业班)向笔者倾诉其在二轮复习教学中的困惑:课堂上少数学生选择自己做题而不听课;教师若简单地梳理思路并用多媒体展示答案收效甚微,若在黑板上完整板书浪费时间,好像也没有必要(学生手里有参考答案);简单、中档题教师不讲学生也会,难题教师讲了学生还是不会;二轮复习时间短(一个月左右),任务重(内容多),如何做到(知识、思想方法、解题策略等)全面撒网,重点捕捉等等.教师C的困惑反映了大多数教师复习备考时的迷茫:复习课,尤其是第二轮复习(一些学校还有第三轮复习)的抓手在哪里?如何提高复习课教学效率?笔者观摩了教师C以“导数与函数的单调性、极值、最值”为题的二轮专题复习课,下面谈谈笔者对问题的理解,并给出教学思考.
一、教学片断简析
例1(2016年高考数学天津卷理科第20题)设函数f(x)=(x-1)3-ax-b,x∈R,其中a,b∈R.
(1)求f(x)的单调区间;
(2)若f(x)存在极值点x0,且f(x1)=f(x0),其中x1≠x0,求证:x1+2x0=3;
(3)设a>0,函数g(x)=|f(x)|,求证:g(x)在区间[0,2]上的最大值不小于
学科组统一的学案在上课前1-2天发给学生,供学生独立思考、合作交流.学生思考(实则是对解答过程的回忆)约两分钟后,教师引导学生回顾判断函数单调性的步骤与作用、函数的极值与最值的概念、确定函数在闭区间上最值的方法,启发学生思考为什么要对参数进行讨论?如何确定参数的分类标准?问题的解答展示如下:
解:(1)由f(x)=(x-1)3-ax-b,得f′(x)=3(x-1)2-a.下面分两种情况讨论:
①当a≤0时,f′(x)≥0恒成立,所以f(x)的单调递增区间为(-∞,+∞),无单调递减区间.
当x变化时,f′(x),f(x)的变化情况如下表:

姨x-∞,1-3a% 331-3a%姨姨3,1-3a% 3 331+3a%姨姨331+3a%姨31+3a% 33 3,+∞f′(x)+0-0+ f(x)单调递增极大值单调递减极小值单调递增
(2)证法1:f(x)存在极值点,由(1)知,a>0,且x0≠1,由题意,得f(′x)0=3(x0-1)2-a=0,即(x0-1)2=,进而(fx)0=
又(f3-2x0)=(2-2x0)3-a(3-2x0)-b=(1-x0)+2ax0-3a-b=-x--b=(fx),且3-2x≠x,由题意及(1)知,0000存在唯一实数满足f(x1)=f(x0),且x1≠x0,因此x1=3-2x0,所以x1+2x0=3.
(3)证法1:设g(x)在区间[0,2]上的最大值为M,max{x,y}表示x,y两数的最大值.下面分三种情况讨论:

综上所述,当a>0时,g(x)在区间[0,2]上的最大值不小于.
点评:第(2)问证法1逆用函数f(x)的单调性建立自变量的值x1与x0的关系.第(1)问确定函数f(x)存在极值的条件及函数的极值点,由于已知函数f(x)的解析式,故考虑代入求证,若解x1关于a的解析式,过程相对稍烦琐,故尝试消去a建立x1与x0的方程,即得(以x1为主元的)证法2.
证法2:由题意知,a>0,f′(x0)=0,即a=3(x0-1)2.
由(fx1)=(fx0),即(x1-1)3-ax1-b=(x0-1)3-ax0-b,
由x1≠x0,得
代入a=3(x0-1)2,整理得(x1-x0)[x1-(3-2x0)]=0.
因为x1≠x0,所以x1=3-2x0,即x1+2x0=3.
函数f(x)=(x-1)3-a(x-1)-(a+b)的对称中心为(1,-a-b).令h(x)=f(x+1)=x3-ax-(a+b),x∈[-1,1],则h(x)(x∈[-1,1])与f(x)(x∈[0,2])的值域相同.由函数图像知,g(x)在[0,2]的最大值为虑函数的极值与区间端点函数值(极值点与区间端点)的关系可知,参数a的分界点为3与,映射到函数h(x)自变量的值-1,1,-,.对应到函数(fx)中,可得第(3)问证法2.
证法2:由f(2)=1-2a-b,f333=1-3a-b,f313=
(1)讨论f(x)的单调性;
解:(1)(略).
点评:第(2)问不等式的证明转化为对应函数在指定区间上的最值问题来解决.证法1利用两个子函数g(x),h(x)的最小值来估计f(x)的范围.为什么要如此结合?还能怎样构造局部函数?尝试直接对欲证不等式的左右两边的函数求最值,得到证法2.
证法2分别确定函数f(x)与f′(x)在[1,2]上的最小值与最大值,相比证法1,证法2中f(x)-f′(x)的估值更精确,能否直接用作差法证明呢?得到证法3.
记p(x)=x4-x3-3x2-2x+6,x∈[1,2],p′(x)=4x3-3x2-6x-2.
令q(x)=4x3-3x2-6x-2,x∈[1,2],则q′(x)=12x2-6x-6,由q′(x)≥0在区间[1,2]上恒成立知,q(x)在区间[1,2]上单调递增,且q(1)=-7,q(2)=6>0,所以存在x2∈[1,2],使得q(x2)=0.
当x∈[1,x2]时,p′(x)<0;当x∈[x2,2]时,p′(x)>0,即函数p(x)在[1,x2]上单调递减,在[x2,2]上单调递增,且p(1)=1>0,p(2)=-2<0,
所以存在x3∈[1,2],使得p(x3)=0,当x∈[1,x3]时,m′(x)>0;当x∈[x3,2]时,m′(x)<0,即函数m(x)在[1,x3]上单调递增,在[x3,2]上单调递减,且m(1)=2>0,m(2)=-ln2,而2>-ln2>,所以x∈[1,2]时,m(x)≥-ln2>,即原不等式成立.
以上证明中,“设而不求”的量x0,x1,x2,x3均仅在判断相应函数单调性时搭桥铺垫,无需对其所在的区间进一步细化.证法3通过求f(x)-f′(x)的最小值,实现了计算的精确化.
例3设f(x)=(x+1)eax(其中a≠0),曲线y=f(x)在x=处有水平切线.
(1)求a的值;
(2)设g(x)=f(x)+x+xlnx,证明:对任意x1,x2∈(0,1),有|g(x1)-g(x2)| 解:(1)a=-2.(过程略) 记w(x)=xlnx,则w′(x)=1+lnx,由w′(x)=0,得x=,所以函数w(x)在上单调递增,当x∈(0,1)时,w(x)<0,w(1)=0,w,所以 所以对任意x1,x2∈(0,1),|g(x1)-g(x2)|<2e-2+e-1. (两个函数q(x),w(x)的上确界点相同,而下确界点与最小值点不同,等号不能成立) 点评:证法1将函数g(x)分成两个子函数q(x),w(x),分别求导得到函数的最值(或确界,=0),进而估计函数值的范围.不等式证明中要保证放缩的方向性(不等式的传递性)与精确度(解题方式方法的可行性).g(x)的两个子函数q(x),w(x)的值域易求且恰好满足结论,若将函数g(x)分拆为f(x)与h(x)=x+xlnx,其值域分别为范围失控.尝试把g(x)作为一个整体,直接探求其性质,得到证法2. 证法2:对任意x1,x2∈(0,1),有|g(x1)-g(x2)| (若g(x)在(0,1)内存在最大值与最小值,否则用上确界与下确界来代替)由g′ 由g′(x0)=0,得 所以|g(x1)-g(x2)| g(x)在(0,1)上有最小值g(x0),不存在最大值(借助极限思想=1或符号法则,通过比较区间端点函数值确定其上确界),利用闭区间上连续函数的零点定理压缩g′(x)的零点x0(确定值)所在区间的长度,即要控制好“x0的精度”,通过“设而不求”变换g(x0)的结构形式,然后构造函数u(t),利用函数u(t)的单调性估算g(x0)的值,继而利用不等式的传递性进行证明. 例4已知函数f(x)=aex+(2-e)x(a为实数,e为自然对数的底数),曲线y=f(x)在x=0处的切线与直线(3-e)xy+10=0平行. (1)求实数a的值,并判断函数f(x)在区间[0,+∞)内的零点个数; (2)证明:当x>0时,f(x)-1>xln(x+1). 解:(1)a=1,函数f(x)在区间[0,+∞)内无零点.(过程略) (2)证法1:当x>0时,f(x)-1>xln(x+1)等价于 即证:当x>0时,ex-x2+(2-e)x-1≥0.① 设h(x)=ex-x2+(2-e)x-1,则h′(x)=ex-2x+2-e. 设φ(x)=ex-2x+2-e,则φ′(x)=ex-2,当x∈(0,ln2)时,φ′(x)<0,当x∈(ln2,+∞)时,φ′(x)>0,所以φ(x)在区间(0,ln2)上单调递减,在区间(ln2,+∞)上单调递增. 又φ(0)=3-e>0,φ(1)=0,0 所以存在x0∈(0,ln2),使得φ(x0)=0,当x∈(0,x0)∪(1,+∞)时,φ(x)>0;当x∈(x0,1)时,φ(x)<0. 所以h(x)在区间(0,x0)上单调递增,在区间(x0,1)上单调递减,在区间(1,+∞)上单调递增.又h(0)=h(1)= 0,所以,当x>0时,h(x)≥0,当且仅当x=1时,等号成立,即①式成立. 综上所述,当x>0时,f(x)-1>xln(x+1). 点评:不少学生在第(1)问中没有检验直线的平行性,说明学生对两条直线的平行关系认识不到位.第(2)问通过恒等变形,借助常用结论ln(x+1) 证法2:当x>0时,欲证f(x)-1>xln(x+1), 即证ex+(2-e)x-1>xln(x+1). 先证:ex>+x+1(x>0). 记m(x)=ex--x-1(x>0),则m(′x)=ex-x-1. 记n(x)=ex-x-1,n′(x)=ex-1,则n(x)在(0,+∞)上单调递增, 所以n(x)>n(0)=0,函数m(x)在(0,+∞)上单调递增,m(x)>m(0)=0,即ex>+x+1(x>0). ex+,只需(x)在(0,1)上单调递减,在(1,+∞)上单调递增,所以0,即ex+(2-e)x-1>+(3-e)x>xln(x+1),即当x>0时,f(x)-1>xln(x+1). 证法3:先证:ex>+x+1(x>0), 则ex+(2-e)x-1>+(3-e)x. 因为ln2<0.7,e<2.8,所以ln2+e<3.5,即ln2-<3-e,因为x>0,所以有≤ln2-≤x<(3-e)x,故有xln(x+1)≤ 故原不等式成立. 证法2利用ex的泰勒展开式进行放缩,即在f(x)-1与 xln(x+1)之间插入“隔离函数”y=+(3-e)x,证法3以 Φ(1)=0为切入点,利用函数y=ln(x+1)的凹凸性,在+(3-e)x与xln(x+1)之间插入“隔离函数”y=x2+.本题若用直接作差法证明,则对差函数的导数零点的精度要求高而难以实施. 1.教学张弛有度,贵在常变常新 知识与课程不会自动转化为学生的素养,学生(核心)素养的培育必须借助知识的内化过程.教学过程是一种特殊的认识过程,也是一个促进学生身心发展的过程.在教学过程中,教师有目的有计划地引导学生能动地进行认识活动,循序渐进地掌握学科知识与基本技能,以促进学生知情和谐发展.教之道在于“度”,学之道在于“悟”.教什么,教到什么程度,是教师必须思考并准确实施的问题.问题没有难度,学生没有主动思维(机械思考应对),缺乏挑战性导致学生疲倦,挫伤学生学习的积极性;问题难度过大,学生绞尽脑汁思考却劳而无获导致学生知难而退,扼杀学生学习自信心.教师在理解数学、理解教学、理解学生的基础上设计教学,促进学生深度学习(深刻地把握学习内容,深度地参与学习过程,学习就是学生与数学本质的逐步对话的过程).众所周知,知识的本质并不在于它的确定性和稳定性,而在于它的发展性和不断的变化性.复习课遭遇内容学生熟知、方法学生耳熟能详等情况,教师更要明确教学目标,聚焦教学重点与难点,在问题的关键处给出自己独特的见解.试想,老生常谈、千篇一律的说教没有文本详尽,比不上搜题工具的解答精彩,怎么可能激发学生的兴趣!通过变式、改编、整合等不同的方式提高学生对知识、思想方法、解题策略等的认知与理解.如例1第(2)问证法2(主元法)反映了对称与非对称的辩证统一,第(3)问证法2以静制动(运动中的不变性)深化了学生对函数最值概念的理解,能培养学生仔细审题与深刻反思的良好习惯.专题设计一脉相承,思维水平逐步递进.例1操作烦琐,通性通法思维要求不高,例2第(2)问入口较宽,局部法与整体法均可,“设而不求”简单过渡,例3第(2)问局部法与整体法要求精细,凸显思维的高层次性,例4第(2)问关卡重重,需要学生思维灵动,富有创新性. 2.积累活动经验,优化思维品质 数学活动经验,是指学习者参与数学活动的经历以及在数学活动过程中所形成的感性认识、情绪体验和观念意识;在进一步的数学活动中能生长为较高层次的活动经验或知识与技能的数学活动经验,则是基本活动经验.[1]新授课带给学生的认知往往是肤浅的,给予学生的活动经验常常是零散的;复习课要有目的地实现对相关内容认识的深化,活动经验理解的整体化.以解题教学为切入点的复习课教学,解题的目的是什么,通过教学学生要达成什么目标等等.因此,教师选择的题目应该具有强烈的训练意图和思维标志.通过训练,帮助学生唤起对典型问题的记忆,联想相关的数学概念、思想方法和解题经验,形成主动归纳的意识,促进数学知识的迁移和解题经验的积累.教师应在“微专题”的核心精要处进行点拨,实现学生数学活动经验的提升,思维品质的优化.如通过例2,学生强化了局部与整体观念,加深了对“设而不求”方法的理解,提高了思维的广度与深度;通过例3证法2,提高学生的估算意识、计算与推理能力.通过例4,学生明晰不等式证明中的逻辑关系,提高了对代数变形的理解(因何而变,变向何方,如何调整)等.又如,2016年高考数学四川卷理科第21题:设函数f(x)=ax2-a-lnx,其中a∈R. (1)讨论f(x)的单调性; 第(2)问可利用必要性解题策略优化解题过程:f(x) >-e1-x在区间(1,+∞)内恒成立,即g(x)=ax2-ax-lnx-+e1-x>0在区间(1,+∞)内恒成立.由g(1)=0,且g(x)为连续函数,则存在δ>1使得g(x)在区间(1,δ)内不减,故g′(x)≥0在区间(1,+∞)内恒成立,由g(x)为连续函数知,必有g(′1)=2a-1≥0,解得a≥. 3.提升理性素养,形成精准定位 数学学科聚焦思维,特别是逻辑思维、理性思维,理性精神,在培养学生的理性精神上做主要贡献.数学是人类生命高水平活动的真实记录和表现形式,但离不开感性,但最终要回归到理性.教学过程中,先有感性后有理性更有利于认识.精准是数学科学的主要特征.张奠宙教授认为:现代公民的数学核心素养,可以界定为“精准智能思维与行为的养成”.所谓精准,包括:“观测精准”“量化精准”“算法精准”“模型精准”,以及精准美学的欣赏.[2]通过对数据进行分析,形成精准的判断和决策是学生理性素养的重要体现.如例1第(3)问证法2“f(2)-的得到与应用(平均值原理);例3第(2)问证法2,少数学生存在理解困难,教师可用(结构实体)隐喻(收入多算,支出少算,盈余增加)助其渡过难关.又如题: (1)当a=-1时,求函数f(x)的最小值; (2)当a≤1时,讨论函数f(x)的零点个数. 第(2)问可对参数划分,分别探求f(x)的性质,也可用分离参数法求解则,容易判断x-2lnx+2>0,进而确定函数g(x)的图像与性质,结果一目了然.感性有余、理性不足的学生无视g′(x)的分子中的公因式,反复构建函数与求导,沦为缺乏数学模型的机械操作;而理性意识较强的学生求导时能聚焦任务(导函数的正负判断原函数的增加)而不会产生滑过现象. 1.赵思林,赵绪昌.指向学生数学活动经验获取的教学[J].教育研究与评论(中学教育教学版),2016(10). 2.张奠宙.解放思想,也来说说数学核心素养[J].中学数学教学参考(上旬刊),2017(4). 3.蒋燕.让高三复习从“解题困惑”走向“自主理解”[J].中学数学(上),2017(1).
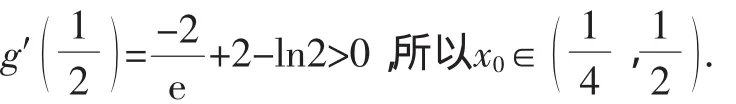
二、教学思考

