大型平台的惯性稳定与地理坐标系姿态跟踪
蒋鸿翔,丁祝顺,王媛媛,卢小东
(北京航天控制仪器研究所,北京100039)
大型平台的惯性稳定与地理坐标系姿态跟踪
蒋鸿翔,丁祝顺,王媛媛,卢小东
(北京航天控制仪器研究所,北京100039)
介绍了一种大型两轴稳定平台的惯性稳定和地理系姿态跟踪原理,建立了稳定平台俯仰框架和横滚框架的运动学模型和动力学模型,进行了稳定平台横滚通道的角速度回路和角位置回路设计,仿真分析了姿态角测量误差作用下的稳定平台姿态跟踪性能,与利用加速度计反馈实现调平的两轴阻尼稳定平台进行对比,比对结果验证了本文设计的控制系统在水平姿态跟踪速度和抗干扰能力上的优势。平台样机进行了姿态跟踪测试,结果验证了结合定位定向系统(POS)的稳定平台惯性稳定和姿态跟踪控制方法可行。
大型稳定平台;运动学模型;动力学模型;惯性稳定;水平姿态跟踪
0 引言
随着大型测量仪器在航空物探、航空遥感等领域的广泛使用,大型惯性稳定平台的应用也越来越广泛。在这些系统中,惯性稳定平台的主要作用是:1)由于飞机在飞行过程中易受气流或者发动机振动等因素影响,产生机体低频角运动与高频线振动,稳定平台可以有效隔离机体运动对载荷测量轴的干扰。2)由于飞机在飞行过程中载荷的水平姿态不为0以及航向始终变化,稳定平台可以实现在一段航线内载荷测量轴对水平及特定航向的自动保持。
目前在国内外航空遥感系统中,基于陀螺稳定的中小型成像相机坐架已实现了商业化[1-2],而在国外海空重力测量系统中,稳定平台的形式正由传统的基于加速度计的阻尼式水平稳定平台,向利用基于组合导航原理的定位定向系统(POS)实现快速姿态跟踪的新型稳定平台发展[3-5]。本文研究的大型惯性稳定平台应用于航空重力测量,为两轴惯性稳定平台。稳定平台自重大,所承载的重力传感器质量也大。驱动装置采用可输出100Nm以上峰值力矩的力矩电机。敏感元件采用POS,基于惯性/卫星组合导航原理,由高性能导航计算机采集陀螺、加速度计和GPS信号,解算得到与其固连的重力传感器在当地地理坐标系下的俯仰、横滚和偏航姿态角数据,并与陀螺测量的惯性空间角速度数据一起,通过高速串行通信传输给稳定平台控制计算机,实现陀螺稳定和水平姿态跟踪控制。
本文将在惯性稳定平台控制建模、陀螺稳定回路和姿态跟踪回路的设计等方面,对大型惯性稳定平台动态环境下惯性稳定及水平姿态跟踪控制进行探讨。
1 稳定平台控制模型
稳定平台的框架由内至外分别为俯仰(与重力传感器和POS固连)、横滚、基座、底座框架结构。稳定平台控制回路包括横滚、俯仰2个通道。横滚和俯仰框架运动范围均小于±10°。基座与底座通过阻尼减振器相连。稳定平台框架结构与框架坐标系示意如图1所示。
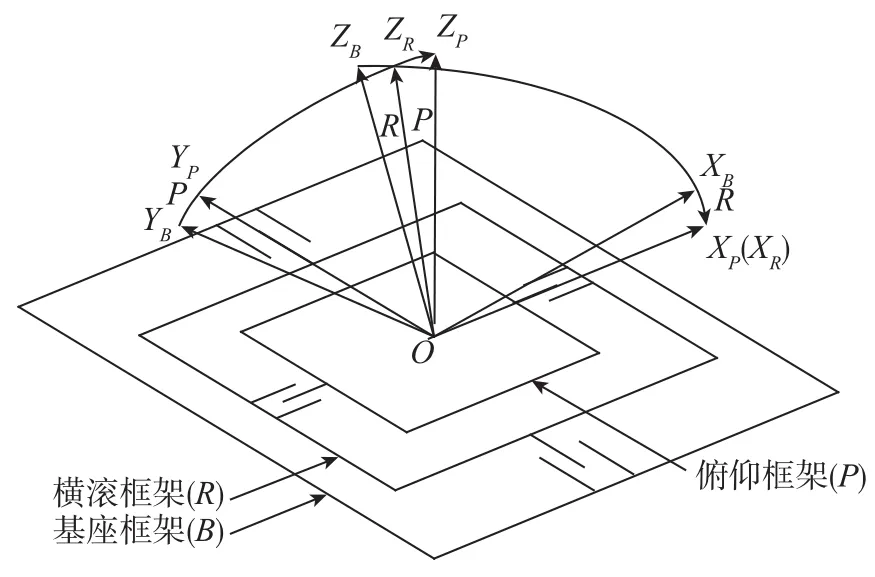
图1 稳定平台框架坐标系图Fig.1 Gimbals and coordinate diagram of the stabilization platform
其中,OXBYBZB为与基座框架固连的坐标系,OXRYRZR为与横滚框架固连的坐标系,OXPYPZP为与俯仰框架固连的坐标系。
俯仰框架的角速度[ωPXωPYωPZ]与受控角运动[ωPXωRY]及基座角运动[ωBXωBYωBZ]的运动学关系如下:
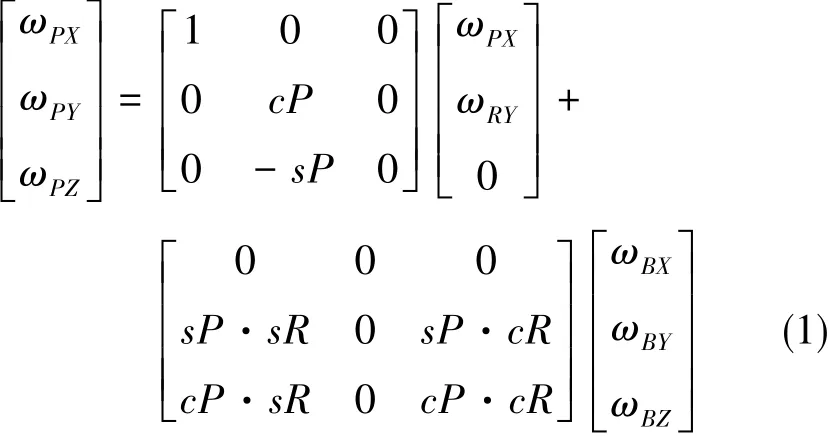
其中,cP=cosP,sP=sinP,cR=cosR,sR=sinR。P为框架俯仰角,R为框架横滚角。
由式(1)可知,这一两轴稳定平台实现框架惯性稳定的条件是:

由ωPY=0可得:

结构设计保证了稳定平台在俯仰框架角变化范围内不会出现cP为0的框架锁定现象,因此式(3)可以满足。俯仰框架的Z轴由于没有运动自由度,其角速度直接与基座角速度相关。
忽略角速度的乘积项,则俯仰框架的动力学方程如下:

其中,JPX为俯仰框架绕XP轴的主惯性矩,TP为俯仰电机输出转矩,fP为俯仰轴上的摩擦力矩、质量不平衡力矩等。
忽略角速度的乘积项和载体的角加速度,则横滚框架的动力学方程如下:
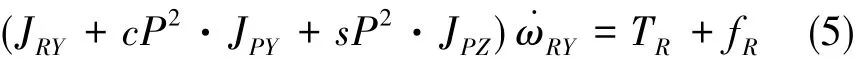
其中,JRY为横滚框架绕YR轴的主惯性矩,JPY和JPZ为俯仰框架绕YP、ZP轴的主惯性矩,TR为横滚电机输出转矩,fR为横滚轴上的摩擦力矩、质量不平衡力矩等。
POS内部包括捷联惯性导航部分和GPS导航部分,捷联惯导选择本地水平指北坐标系(简称N系)为导航解算的数学平台坐标系。OXNYNZN为本地地理坐标系,YN轴指向正北,XN轴指向正东,ZN轴由右手法则确定。俯仰框架坐标系(P系)也是POS基座坐标系,N系到P系的坐标转换关系如图2所示。
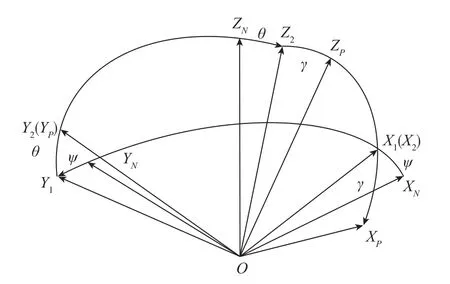
图2 地理坐标系与POS基座坐标系关系图Fig.2 Relationship diagram of POS base coordinate and local geographic coordinate
其中,航向角ψ为YP轴与YN轴的夹角,在水平面XNYNO上测量。俯仰角θ为YP轴与水平面的夹角,在垂直面Y1ZNO上测量。横滚角γ为XP轴与水平面的夹角,在横截面X2Z2O上测量。
由图2可知,当稳定平台控制框架转动实现地理姿态跟踪时,会使俯仰角θ和横滚角γ趋近于0,此时俯仰框架用于安装重力传感器的安装面XPYPO与水平面X1Y1O重合,重力传感器的垂直测量轴平行于ZN轴即当地地垂线。
与航空摄影测量中将差分GPS数据存储和进行事后计算得到高精度位姿数据的POS处理方法不同的是,本文采用的是POS实时输出的姿态数据。POS先进行捷联导航计算,得到捷联姿态矩阵、速度和位置信息。一旦得到更新的GPS信息,执行Kalman状态反馈计算,对捷联解算的位置、速度和姿态角进行反馈修正。这一方法的姿态测量精度较低,但可实时输出修正的姿态信息,适合于平台姿态跟踪控制。
已知从N系到P系之间的姿态矩阵为[6]:

由姿态矩阵可以计算出全部姿态角为:
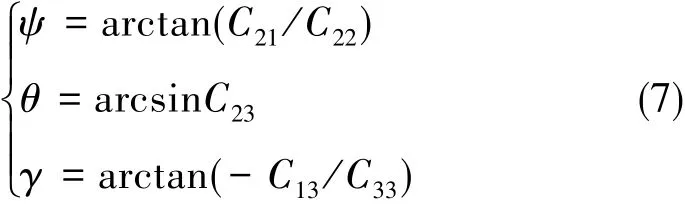
其中,Cij代表其姿态矩阵内部元素,i为行号,j为列号。
为简化控制模型,将POS输出姿态环节用陀螺角速度的直接积分进行模拟,最终稳定平台的两通道总控制模型如图3所示。

图3 稳定平台控制模型Fig.3 Total control model of the stabilization platform
其中,T1和T2为3×3矩阵。GPS(s)和GRS(s)为俯仰和横滚稳定回路控制器,GPA(s)和GRA(s)为俯仰和横滚姿态跟踪回路控制器。rP和rR为俯仰和横滚跟踪回路的输入姿态角指令,为实现水平姿态保持,令其为0。Kg和KP分别为角速度和姿态角环节的比例因子。
2 控制回路设计与仿真
稳定平台的控制回路采用内环为速度环、外环为位置环的双回路控制方案。在典型双回路控制系统中,角速度回路的主要作用是提供角速度阻尼以抑制干扰力矩,同时快速响应角位置回路的输出。而角位置回路的主要作用是改变系统的角位置,使其精确地随动输入的角位置指令。稳定平台由于采用POS陀螺的角速度作为惯性空间角速度反馈信息,采用POS导航解算姿态作为角位置反馈信息,因此可以实现稳定平台在惯性空间内的速率稳定和水平姿态跟踪。
由于稳定平台2个通道的控制相互独立,以横滚通道控制回路设计为例,其原理框图如图4所示。

图4 横滚通道控制回路原理框图Fig.4 Principle control loop diagram of roll channel
其中,K1为PWM驱动及电机环节的比例因子,τ1为驱动环节时间常数,τ2为POS速率采样和姿态解算环节时间常数。J为绕横滚轴的转动惯量。ns为陀螺速率信号干扰,nA为POS姿态信号干扰。由于稳定平台自身结构特点,cP基本等于1,可以不需要在回路中补偿由于俯仰角变化造成的角速度回路增益变化。
角速度回路控制器GS(s)和角位置回路控制器GA(s)均采用比例-积分式。角速度回路的控制带宽主要受惯性稳定平台的结构谐振频率的限制,将开环剪切频率设计为6Hz~8Hz,能够克服典型的频带在1Hz以下的载体干扰角运动。角位置回路的开环剪切频率需设计为角速度回路的开环剪切频率的1/10甚至更小,本文设置为0.3Hz~0.4Hz。由于POS更新角速度和姿态角信息的频率为100Hz,对2条控制回路相位裕度减小的影响均可忽略。
由图4可知控制回路中的干扰项包括:
1)平台轴端干扰力矩fR;
2)载体角运动ωBX和ωBZ;
3)角速度误差ns;
4)姿态角误差nA。
在fR作用下的横滚角γ为:

其中,分母的第2项为角速度回路的开环传递函数,第3项为角速度的开环传递函数乘以角位置回路的开环传递函数。一般来说,干扰力矩的频率会高于角位置回路的剪切频率,此频率处的角位置回路开环传递函数幅值小于0dB,造成第3项的值小于第2项。由此可知,干扰力矩主要由角速度回路进行抑制,角位置回路也起了一定的抑制效果。分子表明稳定平台的转动惯量也会起到抑制干扰力矩的作用。
令ωB=sP·cP·ωBZ+sP·sR·ωBX,则在ωB作用下的横滚角γ为:

由式(9)可知,2条回路对载体干扰角运动的隔离与对干扰力矩的隔离相似,角速度回路在抑制载体扰动角运动时起主要作用。角速度误差ns与横滚角γ的关系也如式(9)所示。
姿态角误差nA与横滚角γ的关系为:

其中,HS(s)为角速度回路从角速度输入到角速度输出的闭环传递函数,对于角位置回路这一环节可以被简化成HS(s)=1/Kg。
根据角位置回路从姿态角指令输入(姿态角误差输入)到横滚角输出的闭环传递函数,知这一姿态跟踪回路的带宽约为0.4Hz,只要姿态角误差为低频周期信号,且频率低于0.4Hz,就会引起相应的横滚角波动。但是如果姿态角误差仅为瞬时或短时误差(比如载体大机动造成POS在1s~2s内的姿态解算误差),当这一误差消失后,稳定平台会控制横滚角快速趋于0。
传统上采用加速度计进行调平控制的两轴稳定平台[7],为了使加速度计测得的比力只反映台体的倾斜,不受载体运动加速度的影响,必须将加速度计调平回路的带宽尽量降低。由于带宽低,因此一旦回路中有力矩或角速度的瞬时扰动造成的姿态变化,或者是载体瞬时加速度引起的稳定平台水平姿态变化,稳定平台水平姿态的回调时间将会很长。
在仿真中模拟了本文姿态跟踪稳定平台和采用加速度计调平控制的两轴稳定平台(带宽为0.01Hz)。令水平姿态跟踪过程中都因载体加速度而造成了姿态测量误差(脉冲幅值为0.05°,脉冲宽度为20s),姿态误差以及由此造成的平台横滚角控制波形如图5所示。
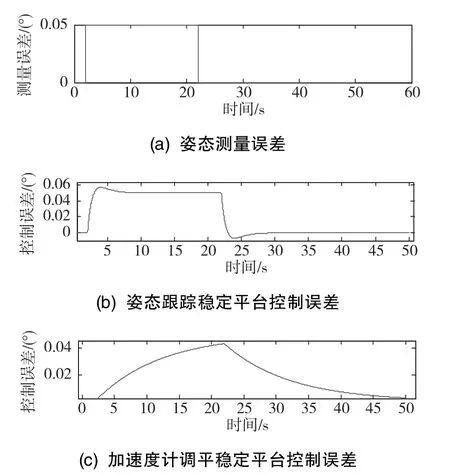
图5 姿态测量误差引起横滚角控制误差图Fig.5 Roll attitude control error caused by attitude measurement error
由仿真结果可以看出,由于本文研究的姿态跟踪稳定平台采用了POS,姿态跟踪回路的带宽较高,这使得姿态跟踪回路能快速且高精度地响应POS输出的地理系水平姿态,实现水平姿态保持。
3 平台样机姿态跟踪测试
稳定平台样机由俯仰框架、横滚框架、基座框架、底座、POS、轴端的测角元件和电机以及控制电路组成如图6所示。模拟重力传感器工装与俯仰框架固连,作为被稳定的台体。基座框架通过减振器与底座框架连接,底座框架再固定于载体上。
为实测平台的姿态跟踪精度,将一台高精度惯组安装在台体上表面中心位置,以测量出平台台体在姿态跟踪回路控制下的实时横滚、俯仰角,其姿态测量精度为0.001°。

图6 稳定平台实物图Fig.6 Physical object picture of the stabilization platform
平台静态条件下,用突然加载配重的方法给横滚控制回路施以约1Nm的常值不平衡力矩,稳定平台横滚姿态控制结果和高精度惯组输出的横滚姿态准确值如图7所示。
由实测数据可知,由于POS陀螺仪自身零偏不稳定、初始对准误差、载体振动引起的陀螺标度因数变化等因素,加之POS根据刷新频率为1Hz的GPS信号进行姿态反馈修正计算的综合结果,造成POS输出姿态总是呈现出周期约1s的锯齿波形式,但在1s其变化范围仅为±0.0015°,相比于干扰力矩来说对姿态跟踪精度影响极小。
总体来说,POS输出姿态与作为姿态基准的高精度惯组输出姿态变化趋势吻合,说明了本文提出的基于POS的稳定平台姿态跟踪控制方法是可行的。
4 结论
本文通过建立大型稳定平台俯仰框架和横滚框架的运动学模型和动力学模型,并以横滚通道为例,分析了角速度回路和角位置回路的控制设计,将为大型稳定平台工程样机控制系统的设计与实现提供理论依据。
通过仿真模拟了姿态测量误差作用下的稳定平台横滚角变化情况,与采用加速度计调平控制的两轴稳定平台水平姿态跟踪效果进行了对比,证实了本文研究的大型稳定平台在姿态跟踪方面的优势。
进行了平台样机姿态跟踪测试,验证了本文提出的结合POS的稳定平台惯性稳定和姿态跟踪控制方法的可行性。
[1]LH System Gmbh.Leica PAV80 gyro-stabilized sensor mount user manual[R].2008.
[2]LH System Gmbh.Leica PAV30 gyro-stabilized camera mount technical reference manual[R].2003.
[3]朱如意,丁祝顺,夏刚.航空重力仪/梯度仪惯性稳定平台研制现状[J].导航与控制,2011,10(2):69-74.ZHU Ru-yi,DING Zhu-shun,XIA Gang.Present state of airbornegravityandgradiometerinertialstabilized platforms[J].Navigation and Control,2011,10(2):69-74.
[4]张昌达.几种新型的航空重力测量系统和航空重力梯度测量系统[J].物探与化探,2005,29(6):471-476.ZHANG Chang-da.Several new types of airborne gravimetric systems and airborne gravity gradiometric systems[J].Geophysical and Geochemical Exploration,2005,29(6):471-476.[5]张永明,盛君,张贵宾.航空重力测量技术的现状及应用[J].勘探地球物理进展,2006,29(2):94-97.ZHANG Yong-ming,SHENG Jun,ZHANG Gui-bin.Status and applications of airborne gravimetry[J].Progress in Exploration Geophysics,2006,29(2):94-97.
[6]高钟毓.惯性导航系统技术[M].北京:清华大学出版社,2012. GAO Zhong-yu.Inertial navigation system technology[M].Beijing:Tsinghua University Press,2012.
[7]Bruton A M,Hammada Y,Ferguson S,et al.A comparison of inertial platform,damped 2-axis platform and strap-down airborne gravimetry[C].International Symposium on Kinematic System in Geodesy,Geomatics and Navigation,Banff,Alberta,2001:542-550.
Inertial Stabilization and Attitude Tracking in the Geographic Coordinate System of the Large Platform
JIANG Hong-xiang,DING Zhu-shun,WANG Yuan-yuan,LU Xiao-dong
(Beijing Institute of Aerospace Control Devices,Beijing 100039)
The principles of inertial stabilizing and geographic coordinate system attitude tracking for a kind of large two-axis stabilization platform are described.The kinematics models and dynamics models of the pitch and roll gimbals of the platform are built.The angle rate control loop and angle position control loop of roll control channel are designed.The simulations of attitude tracking under the condition of the attitude measurement error are done,compared with that of a kind of twoaxis damped stabilization platform utilized the accelerators feedback for horizontal attitude leveling.The result demonstrated that the designed control system in this paper has the advantages in quickly attitude tracking and anti-disturbance capabilities.The attitude tracking test of the stabilized platform prototype was done.Feasibility of the inertial stabilizing and attitude tracking control methods for the stabilizing platform combined with position and orientation system(POS)are demonstrated.
large stabilized platform;kinematics model;dynamics model;inertial stabilizing;horizontal attitude tracking
TP273
A
1674-5558(2017)01-01288
10.3969/j.issn.1674-5558.2017.03.003
蒋鸿翔,男,博士,高级工程师,研究方向为惯性稳定平台控制技术。
2016-06-30

