全姿态惯导系统全方位射向装定技术研究
郭宗本,刘 静,柳 柱,朱志刚
(北京航天控制仪器研究所,北京100039)
全姿态惯导系统全方位射向装定技术研究
郭宗本,刘 静,柳 柱,朱志刚
(北京航天控制仪器研究所,北京100039)
由于增加了随动回路控制,三框架四轴平台系统要完成高精度射向装定必须综合考虑基座倾斜等情况。首先对目前工程上应用的按照框架角进行射向装定的方法应用于三框架四轴惯性平台系统时存在的问题进行了分析,提出了一种基于姿态解算的三框架四轴平台系统精确全方位射向装定新方法,并开展了工程验证与精度对比试验。试验结果表明该方法能够明显提高各种载体条件下射向装定的精度及稳定性,验证了该方法的正确性和工程适用性。
三框架四轴惯性平台;方位轴;俯仰轴;滚动轴;平台框架
0 引言
为了提高导弹武器系统的机动性与制导精度,适应全方位机动发射、全姿态飞行的要求,三框架四轴式惯性平台系统+星光组合导航逐渐取代两框架三轴式惯性平台系统,成为现代惯性平台系统的发展趋势。新一代惯性平台系统应具备高精度的全方位射向装定及对星能力。全方位、高精度射向装定技术是保障惯性平台系统建立高精度初始惯性基准及星光组合制导顺利实施的关键技术环节。
传统工程上采用方位轴姿态角作为判据进行射向装定,但是在三框架四轴平台系统中,由于增加了随动回路控制,采用传统方法进行射向装定时平台系统各框架轴会出现交叉耦合运动,从而带来明显的方法误差。因此,三框架四轴平台系统全方位射向装定技术必须对基座条件及各轴耦合运动进行综合考虑。
本文以某三框架四轴平台为研究对象,首先对目前工程上应用的平台系统全方位装定技术存在的问题进行了分析,根据分析结论提出一种基于姿态结算的三框架四轴平台系统精确全方位射向装定新方法,并开展了工程试验,试验结果充分验证了该方法的正确性和工程适用性。
1 当前射向装定方法
平台系统框架取向如图1所示。OXF轴为内环轴;OYF轴为外环轴,即方位轴;OZF轴为台体轴,即俯仰轴;OX′F轴为随动环轴,即滚动轴。OXPYPZP为惯性坐标系,即台体坐标系;OX′FXFYFZF为平台本体框架轴系,OXbYbZb为载体坐标系。平台台体上的各惯性仪表采用正交配置方案。
目前,该平台采用的全方位装定斜置对星方法为:以平台外环框架角输出θy为锁定回路传感器,装定目标框架角θy=-αe(αe为目标方位角),控制平台台体绕方位轴的转位,采用X向或Y向加速度计输出作为斜置调平回路传感器,控制平台台体绕俯仰轴的转位,采用Z向加速度计输出作为绕滚动轴水平调平回路传感器,控制平台绕滚动轴的转位。

图1 三框架四轴平台框架取向Fig.1 GINS orientation of three frame four axes
将三框架四轴平台系统置于三轴精密位置转台(精度为1″)上,转动平台俯仰轴以模拟平台基座绕弹体俯仰轴的不水平度,按照上述方法,开展了平台系统方位装定及斜置对星试验。试验结果如表1所示。
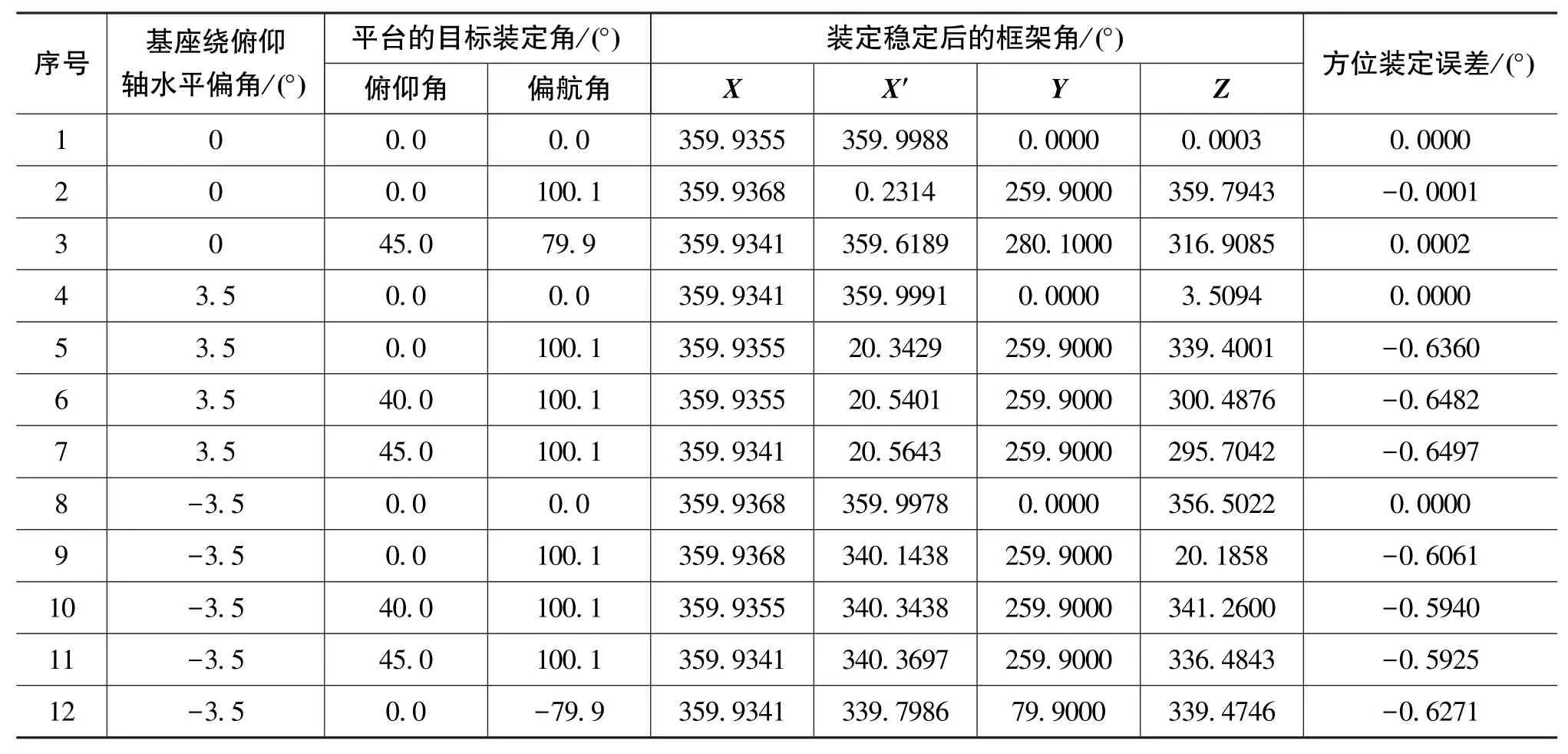
表1 方位装定斜置对星试验结果Table 1 Experiment results of azimuth loading
由表1数据可知,当基座的俯仰水平偏角β0=3.5°,且目标方位α偏离90°±10°时,调平稳定后,随动轴和台体轴框架角输出θx′和θz均偏离0°位置20°左右,即外环轴偏离理想的地理垂线方向20°左右,此时使用外环框架角进行方位装定造成的方法误差可达0.6°左右,无法满足武器系统的射向装定精度要求。
2 当前方法存在的问题及机理分析
假设平台基座绕俯仰轴的不水平角为β0,绕滚动轴不水平角为0,平台要装定的目标方位角和俯仰角分别为αe、βe。
为了便于说明问题,先以一个三轴平台为例说明平台系统全方位装定的过程,假设三轴平台的框架取向如图2所示。
按照上述转位方法,由于作为方位轴的台体轴为最内层框架,考虑到几何约束关系,调平完成后,台体框架轴也被调整到当地地理系的天向,此时依靠台体轴框架角θy作为输入,能够完成精确方位装定。方位装定到位后,以加速度计作为传感器,可在射面内依次完成俯仰方向的转位、锁定、水平调平及斜置调平任务。因此,三轴平台射向装定及斜置对星过程中不存在角运动的耦合,装定精度只取决于平台框架角传感器和加速度计的精度,使用传统射向装定和斜置对星方法不会带来方法误差。
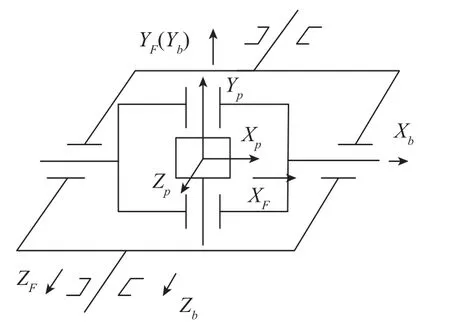
图2 三轴平台框架取向Fig.2 GINS orientation of three frame
在相同的基座条件下,由于在最外层增加了随动环框架,三框架四轴平台系统使用相同的控制算法会产生明显的方法误差。假设此时平台基座沿俯仰方向偏离水平面小角度β0,由于外环框架角装定的角度θy不为0,则平台沿外环轴进动过程中Z加速度计会感受平台基座绕俯仰方向的不水平分量变化,在X轴调平回路的作用下,内环框架角有输出Δθx的趋势,随动框架角则会产生Δθx/cosθy的角度变化用以补偿内环偏角。由于此时外环框架角已偏离零位,因此台体轴不与随动环正交,随动环的角度变化以一定比例投影至台体轴并被Z陀螺仪感受到,进而通过稳定回路及调平回路驱动台体轴框架角产生变化。上述复杂响应的结果为:调平锁定回路达到稳态后,由于随动环在方位装定过程中产生了角度变化,会使外环轴偏离当地地理系天向。表1中的试验结果表明,基座的水平俯仰角β0越大,目标方位装定角越接近±90°,则随动环框架角θx′越大,由此带来的方位装定方法误差也随之增大,因此不能以外环框架角的输出θy作为锁定回路唯一的输入判据。
3 基于姿态解算的全方位射向装定方法
3.1 总体方案
由上一小节的分析可知,若要实现三框架四轴平台系统的精确方位装定及斜置调平,应综合考虑平台台体相对当地水平坐标系的姿态,根据实际姿态与期望姿态的偏差计算各轴加矩量,以保证惯性基准的精确建立。
平台零位置调平锁定建立的坐标系g′系(p0系)为当地地平系,此时台体的Yp轴竖直冲天,XP和ZP两个轴处于当地水平面内,目标方位角、俯仰角、滚动角可认为是相对于g′系(p0系)下的指令角度。因此,可将g′系(p0系)作为转位的惯性参考基准,通过框架角输出、加速度计输出等确定各个时刻平台台体系(控制对象)、各框架系(执行环节)以及p0系(基准环节)的对应关系,以实现两条调平回路以及锁定回路的精确转位控制。
3.2 平台台体系姿态算法
根据平台系统零位置调平锁定稳定时刻的各框架角输出θx0、θy0、θz0、θx′0,可得到平台初始时刻的g′系(p0系)相对于平台基座系b系的姿态矩阵,如式(1)所示。
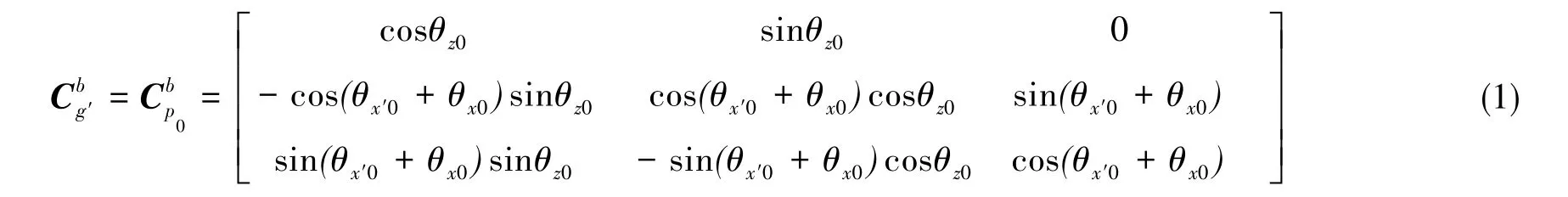
式(1)中已考虑了初始时刻外环框架角θy0的输出应为0的情况。
已知第k时刻平台各框架角的输出θxk、θyk、θzk、θx′k,可得到k时刻平台基座系b系相对于平台台体系pk系的转换矩阵,如式(2)所示。

其中,各元素表达式如式(3)所示。

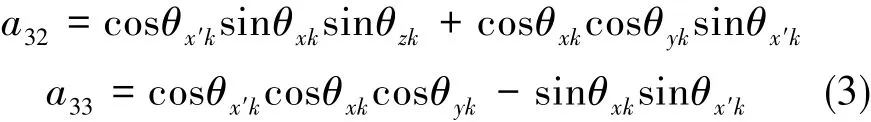
由基准系g′系(p0系)到第k时刻的台体系pk系的方向余弦矩阵如式(4)所示。
设第k时刻的台体系相对于初始基准系g′系的方位转角为αk,俯仰角为βk,滚动角为γk,考虑到平台的滚动角γk始终为0附近的小角度,所以有cosγ>0恒成立。由此,根据方向余弦矩阵与Euler角的转换关系,k时刻台体系相对于g′系的方位转角按照式(5)解算。
k时刻平台的方位角αk距离目标方位角αe的方位偏差如式(6)所示。


平台k时刻的俯仰角及滚动角距离目标位置的偏差角Δβ、Δγ,则可以分别利用相应的加速度计输出进行准确计算。
3.3 转位控制方法
采用3.2节的方法计算出平台台体系距离目标位置偏差角Δα、Δβ、Δγ,利用锁定回路、水平调平回路和斜置调平回路分别计算出陀螺仪加矩控制量,可控制平台台体实现精确转位控制。
由于转位过程中平台台体系的Zp轴始终保持水平状态,因此斜置调平回路与其他回路是解耦的,可以直接利用X或Y加速度计作斜置调平回路的输入,由回路控制律计算出加在Z陀螺仪上的力矩,施加在Zp轴上的力矩电机上实现斜置调平任务。
由上述公式计算出的Δα和由Z加速度计输出的Δγ均是相对地平系g″(平台k时刻所在射面的当地地平坐标系)给出的,由此计算出的锁定加矩电流TA和调平加矩电流TL也是指该系下的加矩值,陀螺仪的实际控制力矩按照式(7)~式(9)进行力矩分解。
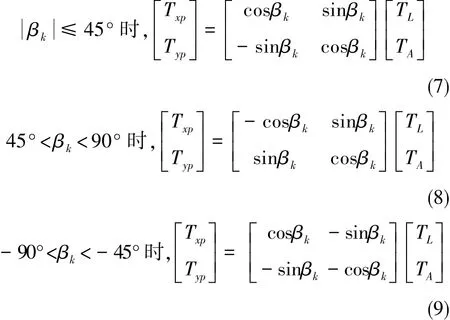
4 验证试验情况
人为设置平台基座处于不同俯仰不水平度下,装定不同的方位角度,使用光学手段测量方位装定误差,对按照框架角进行射向装定的传统方法及本文提出的基于姿态结算的方位装定方法的方法误差进行了验证试验,试验结果如表2所示。
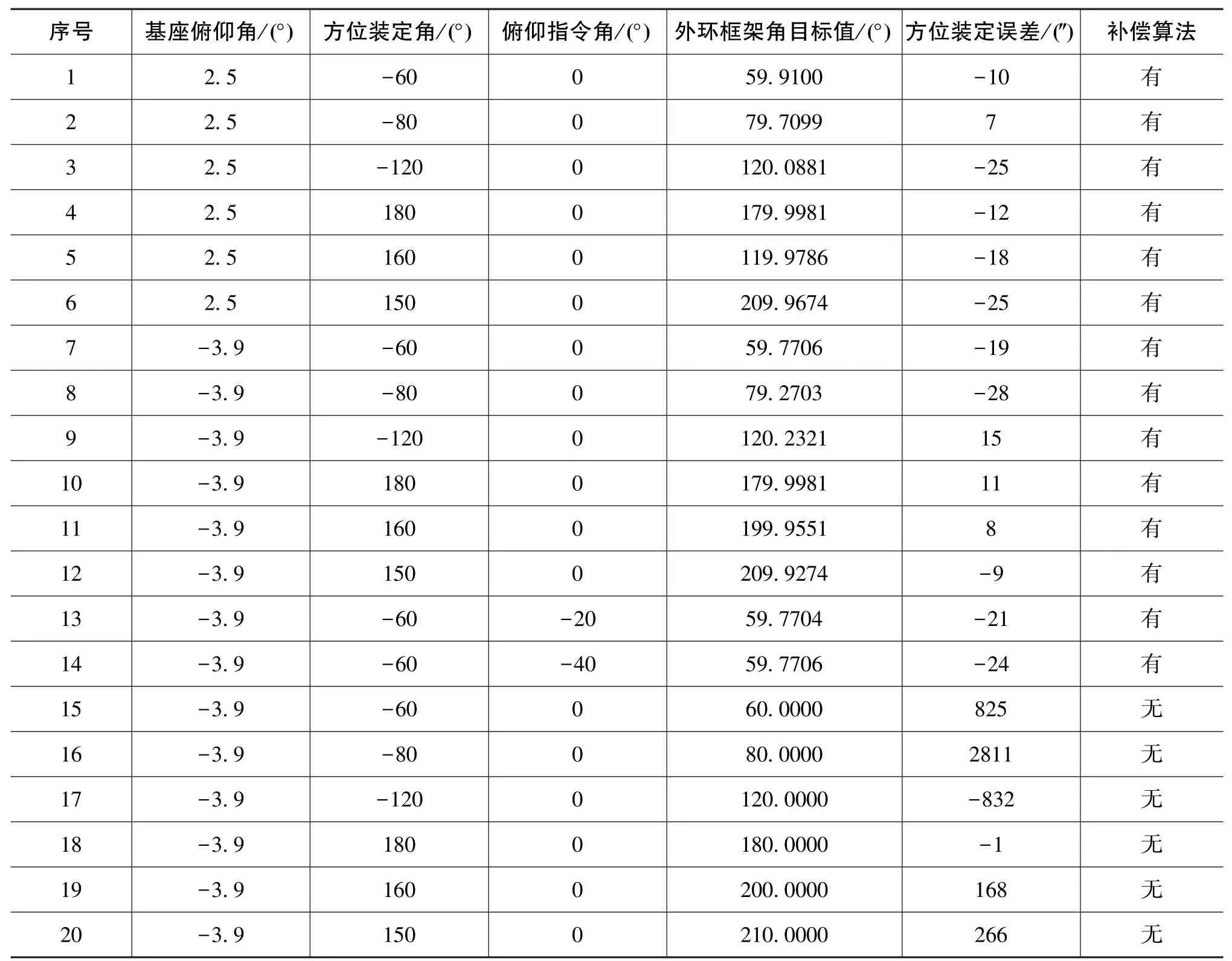
表2 对比验证试验结果Table 2 Results of comparison experiment
由表2可以看出,相对传统装定方法,使用三框架四轴平台系统全方位射向装定方法能够明显提高平台方位装定精度。如表2中的第8项和第16项,基座条件都是低头3.9°,方位装定-80°。采用传统的方位装定方法时,由于转位过程中随动轴角度变化,导致YF轴明显偏离当地垂线方向,造成方位装定误差为2811″;采用本文介绍的全方位射向装定方法,方位装定误差只有28″。这说明本文提出的方法可以较好地规避三框架四轴平台各轴耦合的影响。
另外,当装定相同的方位角而基座俯仰角不同时,本文提出的装定方法可以保持很好的方位装定重复性,3个位置的极差为4.4″,符合预期。
综上可知,利用本方法进行方位装定,最大误差为28″,虽然超过了框架角的标称指标(≤25″),但综合考虑平台初始及当前时刻的调平锁定误差、各轴框架角误差、测量工具误差等因素,试验结果在预期范围内,验证了本方法的正确性。
5 结论
本文针对三框架四轴平台系统全方位射向装定中存在的交叉耦合问题,提出了一种新的基于姿态解算的全方位射向装定技术,并进行了多种状态的验证及对比试验。试验结果表明该方法能够实现在基座倾斜条件下的精确射向装定,有效提高了射向装定功能的环境适应性。
[1]刘静,朱志刚.摇摆条件下惯性平台系统动态特性分析[J].宇航学报,2011,32(9):1878-1883.LIU Jing,ZHU Zhi-gang.Dynamic performance analysis of inertial platform system on rocking base[J].Journal of Astronautics,2011,32(9):1878-1883.
[2]刘静,朱志刚.平台系统多位置测漂自瞄准方案误差分析[J].导航与控制,2008,7(1):15-18.LIU Jing,ZHU Zhi-gang.Error analysis of multi-position drift measure self-alignment scheme of platform system[J].Navigation and Control,2008,7(1):15-18.
[3]刘静,朱志刚.一种空间稳定方式惯性平台导航算法[J].导航与控制,2007,6(3):10-15.LIU Jing,ZHU Zhi-gang.A kind of space stabled inertial platform navigation algorithm[J].Navigation and Control,2007,6(3):10-15.
[4]刘静,朱志刚.惯性平台稳定回路控制律对稳定精度的影响分析[J].导弹与航天运载技术,2012(5):43-46.LIU Jing,ZHU Zhi-gang.Influence on static accuracy of inertial platform caused by the control law of stability loop[J].Missiles and Space Vehicles,2012(5):43-46.
[5]刘静,闫禄,朱志刚.三框架四轴惯性平台建模仿真技术[J].导弹与航天运载技术,2014(1):25-28.LIU Jing,YAN Lu,ZHU Zhi-gang.Four-axes inertial platform simulation technology[J].Missiles and Space Vehicles,2014(1):25-28.
[6]以光衢.惯性导航原理[M].北京:航空工业出版社,1987.YI Guang-qu.The theory of inertial navigation[M].Beijing:Aviation Industry Press,1987.
[7]陆元九.惯性器件(下)[M].北京:中国宇航出版社,1990.LU Yuan-jiu.Inertial devices(2nd)[M].Beijing:China Aerospace Press,1990.
[8]英哲,文钊.陀螺仪理论和设计[M].北京:科学出版社,1977.YING Zhe,WEN Zhao.The theory and design of gyroscope[M].Beijing:Science Press,1977.
[9]杨畅.惯性平台摇摆漂移的机理分析[J].导航与控制,2005,4(1):1-2.YANG Chang.The machanism analysis to the rocking drift of inertial platform[J].Navigation and Control,2005,4(1):1-2.
[10]武凤德,李凤山.高精度惯性导航基础[M].北京:国防工业出版社,2002.WU Feng-de,LI Feng-shan.Fundamentals of high accuracy inertial navigation[M].Beijing:National Defense Industry Press,2002.
Research on Omnidirectional Orienting Technology of all Attitude Inertial Navigation System
GUO Zong-ben,LIU Jing,LIU Zhu,ZHU Zhi-gang
(Beijing Institute of Aerospace Control Devices,Beijing 100039)
For there is a follow-up loop in four-axes stabled inertial platform,the basement incline must be calculated in the process of omnidirectional orienting.In this paper,the problem of the omnidirectional orienting technology of 4-axes stabled inertial platform customarily applied in practice is analyzed.A new precise omnidirectional orienting technology of 4-axes stabled inertial platform is presented.It can calculate the orientation of the platform via real-time angular sensors output.And consequently the experiments approves the correctness and applicability of the 4-axes stabled inertial platform omnidirectional orienting method.
4-axes stabled inertial platform;azimuth axis;pitching axis;rolling axis;platform frames
V448.2
A
1674-5558(2017)01-01238
10.3969/j.issn.1674-5558.2017.03.005
郭宗本,男,硕士,导航、制导与控制专业,高级工程师,研究方向为惯性导航系统设计与研制。
2016-01-26

