金属壳谐振陀螺误差补偿方法研究
付建立
(中航航空电子有限公司,北京100098)
金属壳谐振陀螺误差补偿方法研究
付建立
(中航航空电子有限公司,北京100098)
针对金属壳谐振陀螺的误差建模与补偿方法进行研究。首先,通过分析金属壳谐振陀螺的敏感机理,找到影响陀螺性能的误差源,建立金属壳谐振陀螺的误差模型。然后,研究陀螺的误差传播特性,对误差源进行分类,提出金属壳谐振陀螺的误差补偿方法。最后,利用试验方法对建立的误差模型和补偿方法进行验证。试验结果表明:经过补偿后的金属壳谐振陀螺在工作温度范围内(-45℃~55℃)零偏不稳定性降低至4.67(°)/h,全温度段线性度由0.2%降低至0.03%,随机游走为0.6982(°)/h1/2,陀螺的综合性能得到显著提升,证明了误差模型和补偿方法的有效性。
金属壳谐振陀螺;金属壳谐振子;角速率检测;误差补偿
0 引言
金属壳谐振陀螺主要是利用压电电极的压电效应,来检测振型的运动过程。目前,关于这类轴对称壳谐振陀螺研究最多的是半球谐振陀螺和圆柱振动陀螺,大量学者对这两类陀螺的误差特性进行了研究。Matveev等撰写了关于轴对称壳谐振陀螺的专著,重点研究了半球谐振陀螺,并对该陀螺的模型、信号解算方法、误差特性等进行研究,系统描述了半球谐振陀螺在设计过程中所遇到的问题,为半球谐振陀螺的成功研制奠定了基础。Pi设计了基于非理想参数观测器的漂移补偿方法,利用现代控制理论方法建立半球谐振陀螺的状态空间模型,设计观测器,用于补偿由于模型参数不一致造成的误差。重点描述了在半球谐振陀螺信号解算过程中,如何有效利用控制方法提高解算精度,并未从整体上考虑半球谐振陀螺的误差特性。Wang等则从陀螺的整体出发,建立了半球谐振陀螺的温度模型,并根据温度特性进行了补偿,从而提高了陀螺性能。同时,Wang等还研究了半球谐振陀螺的正交误差抑制方法。而针对圆柱振动陀螺,Innalab公司、Wasston公司均进行了大量研究,包括误差分析与性能提高因素等方面。Loveday、Wu和Kristiansen针对这类陀螺的温度特性、误差特性以及对应的信号补偿方法进行了描述。但是这两类陀螺均为由文献及相关技术资料给出合适的陀螺误差模型和补偿方法。
本文针对金属壳谐振陀螺的误差特性问题进行研究,从金属壳谐振陀螺的敏感机理出发,研究陀螺的误差传播特性,对误差源进行分类,给出金属壳谐振陀螺误差补偿方法。
1 工作原理
金属壳谐振陀螺采取接触式信号激励与采集方式,利用粘贴在振子壁上的压电片,实现信号的解算。金属壳谐振子的四波腹振动,可以沿45°角进行正交分解与合成。因为电极是固定且离散分布的,而振型却是连续和转动的,因此检测电极无法跟踪波腹。所以金属壳谐振陀螺的工作原理并不是直接敏感波腹的运动,而是敏感两个正交振动,再进行合成。金属壳谐振陀螺可等效为一个经典的哥氏振动陀螺,即一个二维弹簧质点运动模型,如图1所示。
在压电电极1和压电电极5所在的xp轴,与电极3和电极7所在的xn轴构成p轴系;电极2和电极6所在的yp轴,与电极4和电极8所在的yn轴构成q轴系。金属壳谐振子的驻波振动,就可沿着x轴系和y轴系进行正交分解。对应的二维弹簧质点运动模型中,每一个轴上都存在着约束力k和阻尼力d。x轴系负责提供振荡源,其中电极1和电极5提供激励信号,电极3和电极7负责检测x轴的实际振动情况;y轴系负责振型偏转检测与振型控制,其中电极4和电极8位于波节点,负责检测振型偏转信号,电极2和电极6负责施加阻尼力矩,使振型向反方向偏转,时间的反向力与输入角速率成正比。
金属壳谐振陀螺在工作过程中处于受迫振动状态,主要振动力由外部激励电极提供。在实际过程中,加入电极激励力,有:
其中,fp=Apsin(ωpt+φp)为p轴系施加的激励力,Ap为激励力的幅值,ωp为施加激励力的频率,φp为施加激励力的相位;fq=Aqsin(ωqt+φq)为q轴系施加的阻尼控制力,Aq为阻尼控制力的幅值,ωq为阻尼控制力的频率,φq为阻尼控制力的相位。
而对于这类振动陀螺而言,激励轴系p轴向上施加的激励力是维持陀螺处于谐振状态的关键。在理想情况下,可认为fp保持不变,认为金属壳谐振子的谐振频率不随外部环境变化,而p轴向上施加的阻尼控制力使实时改变的,其幅值、频率和相位的改变主要取决于陀螺的工作模式。于是,可推导出角速率输出为:
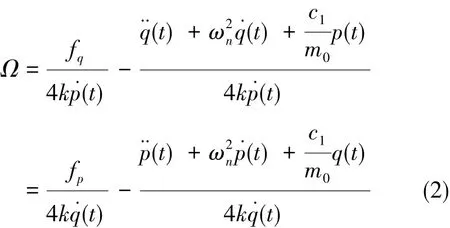
其中,刚性轴系p用于维持振子稳定振动,其轴向上振动位移p(t)受到p轴系施加的激励力fp影响,而提取角速度信息主要依靠q轴系位移。q轴系施加的阻尼控制力fq是为实现力反馈模式解算角速度,在开环模式下也可不施加。在力反馈模式下,角速率信号为:

在实际过程中,这类振动陀螺大多采用力反馈模式。该模式能够提高陀螺整体精度,抑制振型偏移,提高响应带宽。
而对于刚性轴系上的位移p(t)和q(t)而言,主要是利用压电片的压电效应来提取位移信号。
如图2所示,压电单元在金属壳谐振子壁上振动时,对应的电极3和电极7采集轴系p运动位移,对应的电极4和电极8采集轴系q运动位移。由正压电效应可得电极3、电极4、电极7、电极8处产生的电荷量:
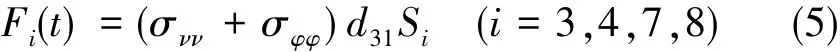
其中,Fi(t)为对应电极产生的电荷量(C),d31为压电元件的压电常数(C/N),Si为对应电荷分布的面积(m2)。利用电荷-电压转换电路,将电荷量转换成电压信号,利用ADC提取电压信息,用于数据处理,于是可得到:
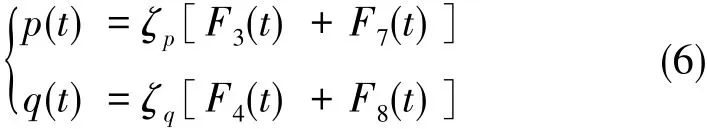
其中,ζp为电荷转换为电压、电极3与电极7进行差分处理后的统一系数,ζq为电荷转换为电压、电极4与电极7进行差分处理后的统一系数。

图2 压电检测示意图Fig.2 Sketch map of piezoelectric detection
对于力平衡模式,需要对信号进行闭环控制,根据检测到的振型偏移信息,动态调节激励力fp和反馈控制力fq,从而使振子出于谐振状态且振型不发生偏移。具体实现如下:位于x轴系的电极1和电极5为激励电极,通过施加频率为金属壳谐振子固有频率的正弦激励信号,使振子产生振动,激励信号由DSP利用DDS算法直接产生,并通过DAC施加到电极1和电极5上。同时,DDS还为信号的幅值和相位解算提供精准的调制信号。通过检测电极3和电极7,来计算实际金属壳谐振子的振动情况,设计幅值回路控制器GA和频率回路控制器GF,动态调整DDS,使金属壳谐振子产生谐振。在此基础上,时刻检测位于y轴系上的电极4和电极8,分析振动驻波的进动情况,同时设计速率回路控制器GR和正交回路控制器GQ,动态调整施加在电极2和电极6的阻尼力矩,使陀螺工作于力平衡模式,振型保持不变。同时,速率控制回路的控制器输出,正比于输入角速率。整体信号流图如图3所示。

图3 电路系统信号流图Fig.3 Signal flow diagram of circuit system
2 误差模型
综合分析结果,可以得出金属壳谐振陀螺的输出角速率信号为:
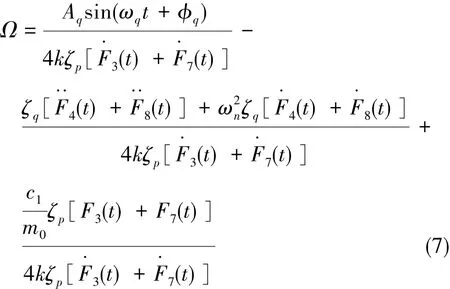
在实现过程中,施加的阻尼控制力幅值Aq、频率ωq以及相位φq均由控制算法决定,而最终输出的角速率应为:

其中,K为对应的阻尼控制力与角速率的比例系数,而K与两个刚性轴系的运动和控制算法有关系。
通过上述分析,金属壳谐振陀螺输出信号的误差源应包含如下几部分:
(1)激励频率ωp与阻尼控制频率ωq不一致
这种不一致称为金属壳谐振子的频率裂解问题,该问题是振动陀螺的固有特性,而对于频率裂解的抑制方法已经进行了大量研究,本文利用激光修形方法,将金属壳谐振子的频率理解抑制在0.1Hz。
(2)激励频率ωp与阻尼控制频率ωq受外界温度发生改变
金属壳谐振子的固有振动频率受材料特性的影响会发生变化,而谐振频率的变化可以靠幅度控制回路和频率控制回路进行跟踪,始终保持金属壳谐振子出于谐振状态,即根据振子频率的变化来调节激励频率,使其能够有效跟踪振子的频率变化。
(3)电路设计过程中,电子元器件性能受外界温度影响
在电路设计过程中,所选用的控制器、运算放大器、AD采集芯片、电容、电阻等都会受到外界环境影响,从而影响陀螺性能。而这种影响是线性化的,可以通过补偿手段进行补偿。
(4)进动因子随外界温度影响
进动因子变化主要是外界环境影响造成振子材料参数发生变化导致,主要会影响陀螺的零位和标度因数,但是这种影响是线性化的,可以通过补偿手段解决。
(5)控制算法解算过程中出现偏差
在离散采样环境中,势必会造成信号解算出现误差,该部分误差可以通过标定解决。
(6)角速率信号输出随机噪声
此噪声为陀螺的典型误差源,可通过补偿手段进行抑制。
(7)壳体振动影响
该影响为不可抗影响,只能在使用过程中,将陀螺本身与被测物体进行固连,并根据情况进行适当的减振处理。
综上所述,金属壳谐振陀螺的误差模型可描述为:

其中,SF(Ω,T)为陀螺整体的标度因数,将振子本身的进动因子随环境变化、电路器件的放大倍数随环境变化进行统一表述,(Ω,T)表示影响因素为输入角速率和温度;Aq(ξ)为控制算法输出,(ξ)表示其影响因素主要受控制算法精度影响;Nu(T)为陀螺输出的零位,其影响因素为温度;v(t)为随机噪声信号。
3 补偿方法
综合式(9)分析影响金属壳谐振陀螺性能的误差源,将其分为3类:零位误差、比例系数误差和随机误差。而对于控制算法造成的误差(ξ)将其影响向下进行传递,认为是标度因数误差,则可将陀螺误差模型可改写成:
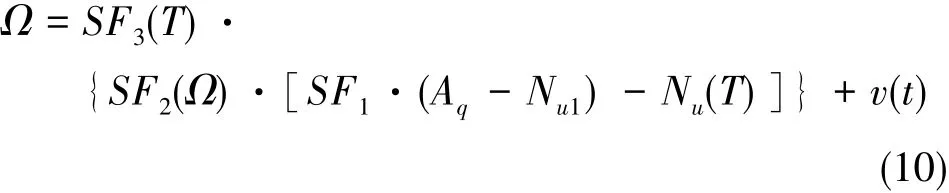
其中,SF1为初步给定的陀螺标度因数,Nu1为初步给定的陀螺的零位。所以,可将金属壳谐振陀螺误差补偿分为:
1)粗补偿,即确定SF1和Nu1;
2)零位补偿,即确定Nu(T);
3)标度因数补偿,即确定SF(Ω,T);
4)随机误差补偿,即补偿v(t)影响。
3.1 硬件实现过程
在电路系统的硬件实现上,控制回路、DDS信号产生由DSP完成,信号采集由ADC完成,信号输出由DAC完成,压电电极的激励与检测利用搭建的模拟调理电路完成。在施加电路系统的设计中,DSP芯片选用STM32F405,ADC由DSP提供,DAC芯片选用AD5328,模拟调理电路的核心器件选用OPA2227。
综上所述,将电路系统分为3部分内容:驱动组件、检测组件和控制回路。其中,驱动组件包括DDS算法设计、压电电极的激励信号调理,检测组件包括压电电极输出小信号的调理、幅值相位的解算,控制回路包括幅值控制回路、频率控制回路、速率控制回路和正交控制回路。而在硬件实现上,电路系统包括3个部分:电源电路、信号处理电路和信号解算电路。电源电路负责电路的整体供电,其中信号处理电路采用±15V供电,信号解算电路采用5V供电。电路系统整体框图如图4所示。
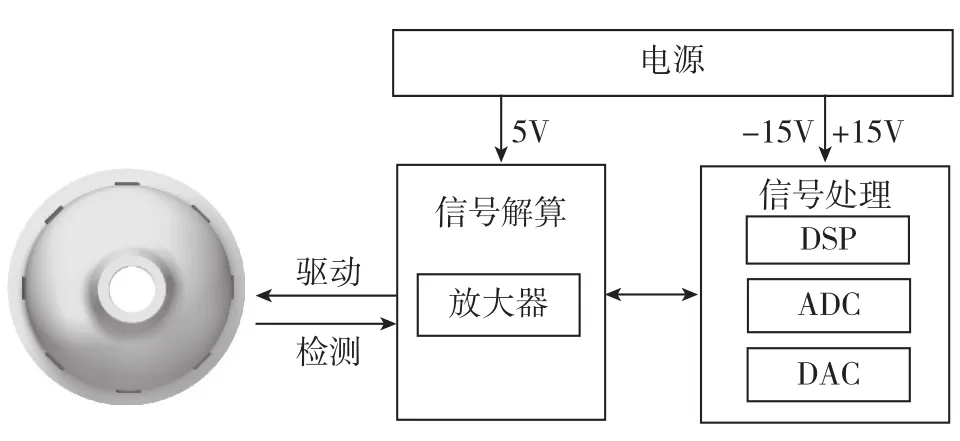
图4 电路系统整体框图Fig.4 Structure diagram of circuit system
3.2 粗补偿
将金属壳谐振陀螺置于隔振转台上,保持陀螺静止,将控制幅值Aq直接输出,利用工控机记录陀螺输出数据,记录时间为5min,设计陀螺输出的更新时间为10ms,控制转台以+100(°)/s的角速率运动,记录陀螺仪输出,输出曲线如图5所示。
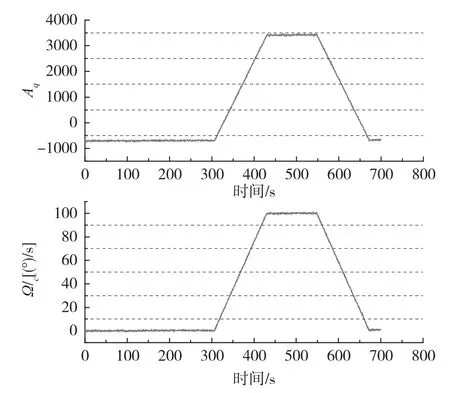
图5 金属壳谐振陀螺粗补偿输出曲线Fig.5 Coarse compensated output curve of metal shell vibratory gyro
由图5可知,陀螺在粗补偿情况下的陀螺零位值为-703.3858(前5min数据取平均),比例系数为0.0242,经过此步骤后,陀螺粗补偿后的输出如式(11)所示:

3.3 零位补偿
将金属壳谐振陀螺置于带有温箱的转台上,保持转台静止。将温箱温度设定为-45℃,保温2h。控制温箱以2℃/min的升温速率,升至55℃,然后在55℃情况下保温2h。在此过程中,记录温度变化过程中粗补偿后陀螺数据和温度传感器输出数据,输出数据更新率为100ms,输出的陀螺粗补偿后数据和温度传感器数据如图6所示。
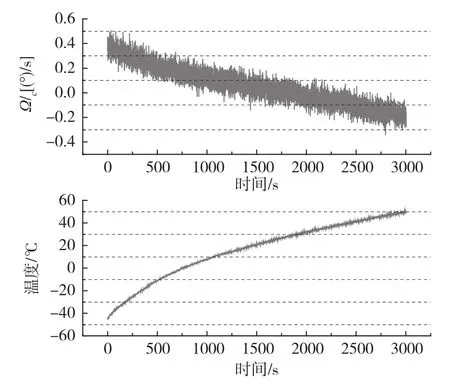
图6 试验测试数据Fig.6 Test data of experiment
利用2阶最小二乘方法进行温度零位补偿,补偿过程如式(12)所示,补偿效果如图7所示。经过温度零位补偿后,在工作温度范围内,陀螺零位的试验标准差由0.1624(°)/s降低至0.0619(°)/s。

图7 零位补偿前后效果对比Fig.7 Comparison of zero bias before and after temperature compensation
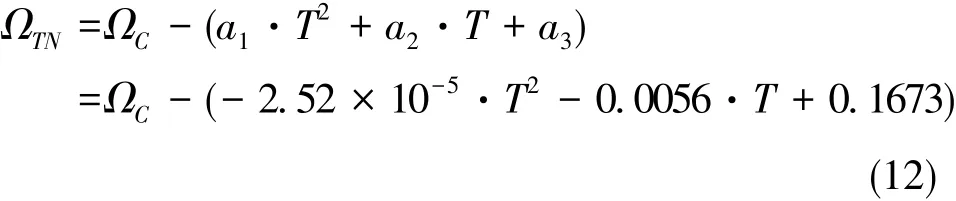
3.4 标度因数补偿
标度因数补偿主要涉及两个因素,一个是外部输入角速率,一个是温度。首先在恒定室温环境下,研究影响因素为输入角速率的补偿。通过测试发现,外界输入角速率越大,陀螺输出的标度因数偏差越大,如图8所示。用于本次测试的金属壳谐振陀螺的量程为±360(°)/s,当陀螺运行于-360(°)/s时,其实际输出为-361.4(°)/s,由图9可以算出陀螺的线性度为0.2%。
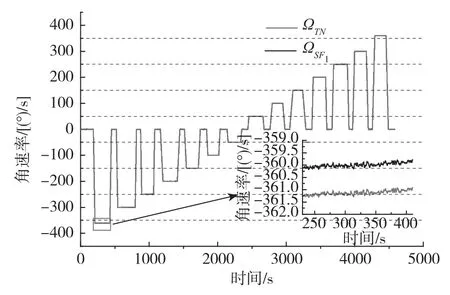
图8 标度因数受输入角速率影响时域图Fig.8 Time domain diagram of scale factor is affected by the input angular velocity
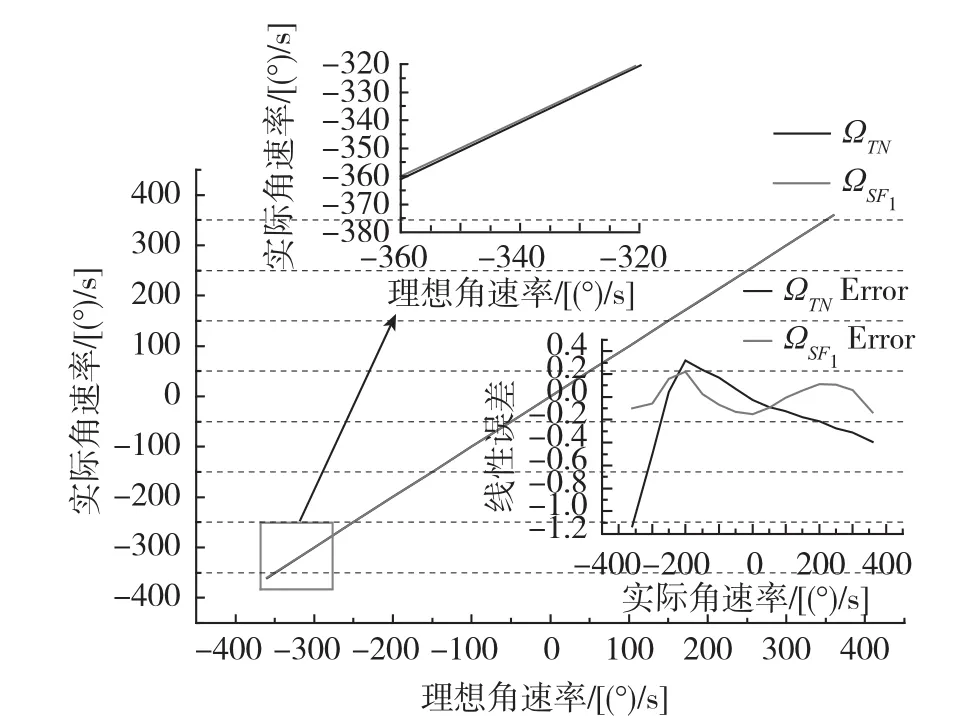
图9 标度因数受输入角速率影响补偿后线性度分析Fig.9 Linearity analysis after compensation of scale factor is affected by the input angular velocity
利用2阶最小二乘方法,对金属壳谐振陀螺的标度因数关于输入角速率的影响进行补偿,补偿后的结果如图8和图9所示,补偿后线性度为0.03%。
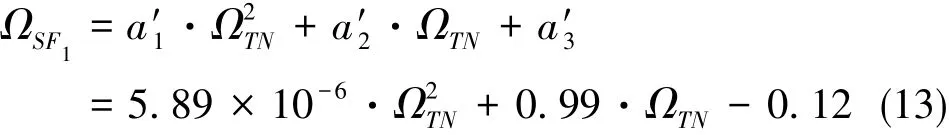
接下来研究温度对标度因数的影响,将陀螺置于温控转台上以300(°)/s的转速转台,同时控制温箱从-45℃升温至+55℃。测试结果如图10所示。由图10可知,金属壳谐振陀螺的标度因数随着外界温度的升高而降低。
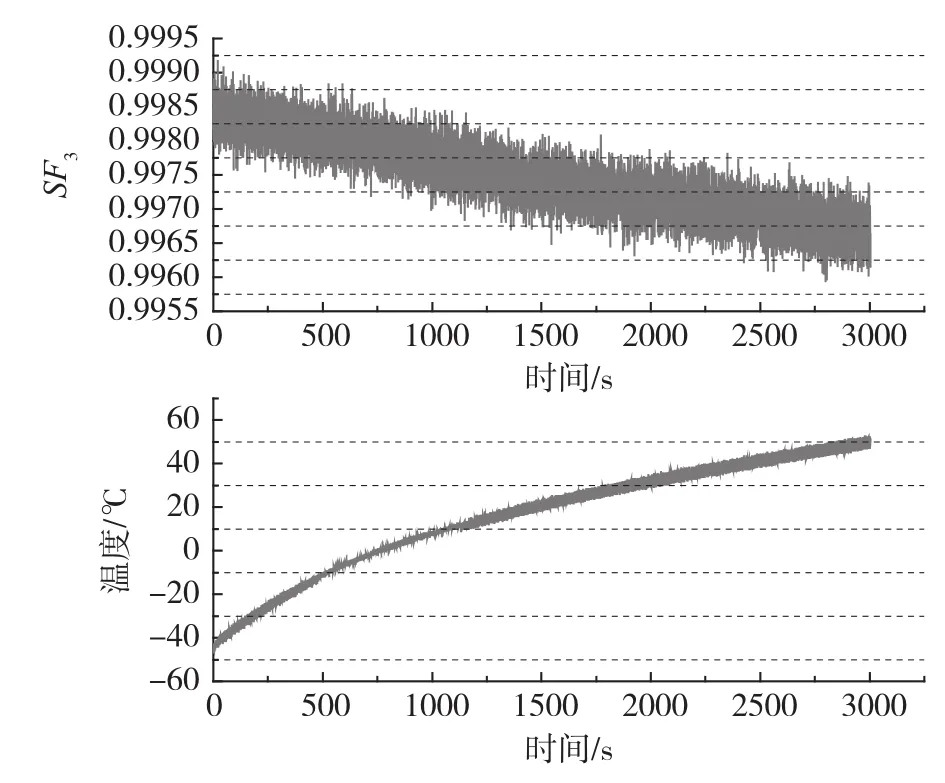
图10 标度因数随温度变化曲线Fig.10 Scale factor curve varies with temperature
同样利用2阶最小二乘方法,对标度因数受温度的影响进行补偿,补偿过程如式(14)所示,补偿结果如图11所示。补偿前,在工作温度范围内,金属壳谐振陀螺工作在300(°)/s时的试验标准差为0.1663(°)/s,经过补偿后,试验标准差为0.0638(°)/s。

图11 标度因数随温度变化补偿结果Fig.11 Compensation results of scale factor varies with temperature
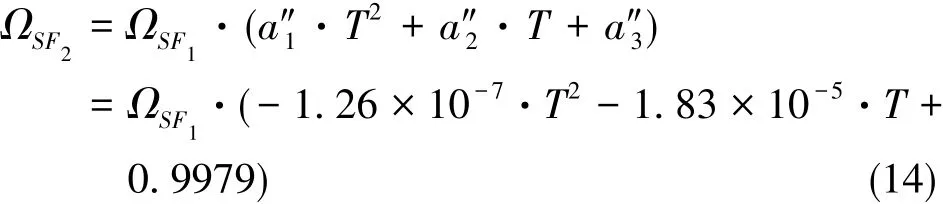
3.5 随机误差补偿
经过粗补偿、零位补偿和标度因数补偿后,认为陀螺输出的误差还包含有随机误差,研究金属壳谐振陀螺的随机误差补偿。利用FIR低通滤波器,进行输出信号的随机误差的补偿。设计的FIR滤波器截止频率选为200Hz,阶数为50阶。将金属壳谐振陀螺至于温箱中,控制温箱从-45℃升温至+55℃,验证温度补偿、随机误差补偿效果,如图12所示,信号噪声幅度明显降低。计算陀螺输出的Allan方差,如图13所示。得到陀螺的零偏不稳定性为4.67(°)/h,角速率随机游走为0.6982(°)/h1/2。
4 结论
本文重点针对金属壳谐振陀螺的误差建模与补偿方法进行研究。首先,通过分析金属壳谐振陀螺的敏感机理,找到影响陀螺性能的误差源,建立金属壳谐振陀螺的误差模型。然后,研究陀螺的误差传播特性,对误差源进行分类,提出金属壳谐振陀螺的误差补偿方法。最后,利用试验方法对建立的误差模型和补偿方法进行验证,试验结果表明,经过补偿后的金属壳谐振陀螺在工作温度范围内(-45℃~55℃)零偏不稳定性降低至4.67(°)/h;全温度段线性度由0.2%降低至0.03%;随机游走为0.6982(°)/h1/2,陀螺的综合性能得到显著提升,证明了误差模型和补偿方法的有效性。
但是,对于传统的轴对称壳谐振陀螺来讲,金属壳谐振陀螺的相关指标较低,尤其是零偏不稳定性和随机游走指标。在后续的研究中,将加强这方面性能的研究。除此之外,还应继续深化对金属壳谐振子数学模型的研究,考虑压电电极、粘接影响等;同时,考虑将金属壳谐振陀螺利用非接触方式进行信号激励与检测,消除在钟壁上粘贴压电片而产生的误差,但改为此方式以后,工艺性和成本都将增加。
[1]IEEE 1431-2004.IEEE standard specification format guide and test procedure for coriolis vibratory gyros[S].New York:Institute of Electrical and Electronics Engineers,2014.
[2]Watson W S.High Q angular rate sensing gyroscope[P].US Patent:US6550329,2003-04-22.
[3]Chikovani V V,Yatzenko Y A,Kovalenko V A.Coriolis force gyroscope with high sensitivity[P].US Patent:US7513156,2009-04-07.
[4]谢笛.杯形波动陀螺数字化测控技术研究[D].国防科学技术大学,2011.XIE Di.The study on cupped wave gyro digital measure and control technology[D].National University of Defense Technology,2011.
[5]Armenise M N,Ciminelli C,Dell'Olio F,et al.Advanced in gyroscope technologies[M].Berlin:Springer,2013.
[6]Kristiansen D.Modeling of cylinder gyroscopes and observer design for nonlinear oscillations[D].Norwegian University of Science and Technology,2000.
[7]Leland R P.Adaptive tuning for vibrational gyroscopes[C].IEEE Conference on Decision and Control,2001:3447-3452.
[8]Batur C,Sreeramreddy T,Khasawneh Q.Sliding mode control of a simulated MEMS gyroscope[C].Proceedings of the American Control Conference 2005,IEEE,2005:4160-4165.
[9]Fei J,Ding H.Adaptive sliding mode control of dynamic system using RBF neural network[J].Nonlinear Dynamics,2012,70(2):1563-1573.
[10]Liu N,Su Z,Li Q.Design and experiment of a novel bell-shaped vibratory gyro[J].Sensors and Actuators A:Physic,2016,238:37-50.
[11]Shatalov M Y,Lunin B S.Vibratory gyroscopes:identification of mathematical model from test data[C].14thInternational Conference on Integrated Navigational Systems(CINS),2007.
[12]Prikhodko I P,Trusov A A,Shkel A M.Compensation of drifts in high-Q MEMS gyroscopes using temperature selfsensing[J].Sensors and Actuators A:Physical,2013,201:517-524.
[13]刘金琨.系统辨识理论及MATLAB仿真[M].北京:电子工业出版社,2013.LIU Jin-kun.System recognition and simulation of MATLAB[M].Beijing:Electronics Industry Press,2013.
[14]Su Z,Liu N,Li Q,et al.Research on the signal process of a bell-shaped vibratory angular rate gyro[J].Sensors,2014,14(3):5254-5277.
[15]严恭敏.惯性仪器测试与数据分析[M].北京:国防工业出版社,2012.YAN Gong-min.Inertial device test and data analysis[M].Beijing:National Defense Industry Press,2012.
Research on Error Compensation of Metal Shell Vibratory Gyro
FU Jian-li
(AVIC Avionics Co.,Ltd,Beijing 100098)
The method of error modeling and compensation for metal shell vibratory gyro is studied.Firstly,by analyzing the sensitive mechanism of metal shell vibratory gyro,the error source that affects the performance of gyro is found,and the error model of metal shell vibratory gyro is established.Secondly,the error propagation characteristic of gyro is studied,and the error source is classified.The error compensation method of metal shell vibratory gyro is put forward.Finally,using the test method to verify the error model and compensation method,experimental results show that after the metal shell vibratory gyro compensated in the working temperature range(-45℃~55℃)bias instability is reduced to 4.67(°)/h,the entire temperature linearity is reduced from 0.2%down to 0.03%,random walk 0.6982(°)/h1/2,the comprehensive performance of the gyro has been significantly improved,proves the validity of the error model and compensation method.
metal shell vibratory gyro;metal shell resonator;angular velocity measurement;error compensation
TP212.1
A
1674-5558(2017)02-01411
10.3969/j.issn.1674-5558.2017.03.007
付建立,男,计算机科学专业,研究方向为飞行器导航、飞行模拟及数据分析等。
2017-05-13

