基于多场耦合的旋转圆盘电极法研究酸性镀铜

冀林仙*，聂合贤，苏世栋，陈苑明，何为

（1.运城学院，山西 运城 044000；2.电子科技大学，四川 成都 610000）

【研究报告】

基于多场耦合的旋转圆盘电极法研究酸性镀铜

冀林仙1,*，聂合贤1，苏世栋1，陈苑明2，何为2

（1.运城学院，山西 运城 044000；2.电子科技大学，四川 成都 610000）

采用多物理场耦合方法建立了旋转圆盘电极(RDE)电镀酸铜的模型，分析了电解池内不同RDE转速下的流场分布与扩散层分布特征，探讨了镀铜过程中RDE的转速及尺寸对电极表面电流密度与镀层厚度分布的影响，为电镀件表面电流密度分布和镀层厚度均匀性的研究提供理论指导。

酸性镀铜；旋转圆盘电极；多物理场耦合；电流密度分布；厚度均匀性；数值模拟

功能化、集成化、小型化和高可靠性的电子信息产品，要求作为搭载元器件、功能模块以及芯片实现电气互连的印制电路板(PCB)向高密度化、高可靠性方向发展。高密度互联(HDI)印制电路板的线路微细化使得PCB产品层数增加，而导通孔的直径减小[1-2]。因此，印制电路板层间互连孔金属化品质、板面电镀铜性能就成为了PCB产品高可靠性的关键。电镀铜作为HDI板制造的关键技术，其镀液稳定性和铜镀层均匀性一直是电镀铜互连研究的热点[3-4]。近年来，酸性镀铜液中加速剂、抑制剂、整平剂等添加剂的协同作用机制已经被大量研究[5-7]。结果表明，镀液中加入添加剂能改善镀层均匀性和镀层质量，而且镀液流动方式对电镀速率与镀层均匀性影响较大，尤其是不同对流方式下，整平剂的吸附状态会影响镀层性能[8-9]。实验中常用旋转圆盘电极(RDE)来模拟镀液不同对流条件下金属电沉积的电化学行为并加以比较，分析电沉积过程中添加剂的作用机理。但电镀时，RDE表面电流并非均匀分布，不能够反映整体电镀件的综合电镀效果，进一步描述真实电镀槽的电镀效果。为了描述RDE的电镀机理，本文在高性能计算机和数值模拟软件Comsol Multiphysics的帮助下，采用多物理场耦合方法对RDE电镀铜的槽内对流、电极表面一次、二次与三次电流分布进行数值模拟，以求反映真实电镀槽的电镀情形，提供电镀过程清晰的图形化结果，反映电沉积过程的真实机制，为电镀工件镀层均匀性的研究提供理论指导。

1 多场耦合模型

酸性镀铜以硫酸铜、硫酸和氯离子作为电解质溶液，在直流电作用下，金属中的电子与镀液中的铜离子在电场作用下发生定向迁移，铜离子移动到阴极，在阴极表面得到电子并还原为金属铜单质，沉积在阴极表面。整个电镀铜过程中，电镀液与金属接触面发生电化学反应，形成阴极不断变化的沉积边界，作用机理如图1。

图1 电镀铜作用机理Figure 1 Mechanism of copper electrodeposition

分析整个电镀铜过程，包括电场、流场、压力场、化学反应、物质传递与传热等多个物理场与物理过程，这些物理过程之间相互作用，协同影响铜在阴极的沉积[10]。电镀铜的各个物理过程都可以用偏微分方程来描述，通过物理参数进行方程之间的关联，获得电镀铜过程中镀液流场分布、电极电流分布与镀层厚度变化等特征。电镀铜物理过程之间的耦合关系如图2所示。

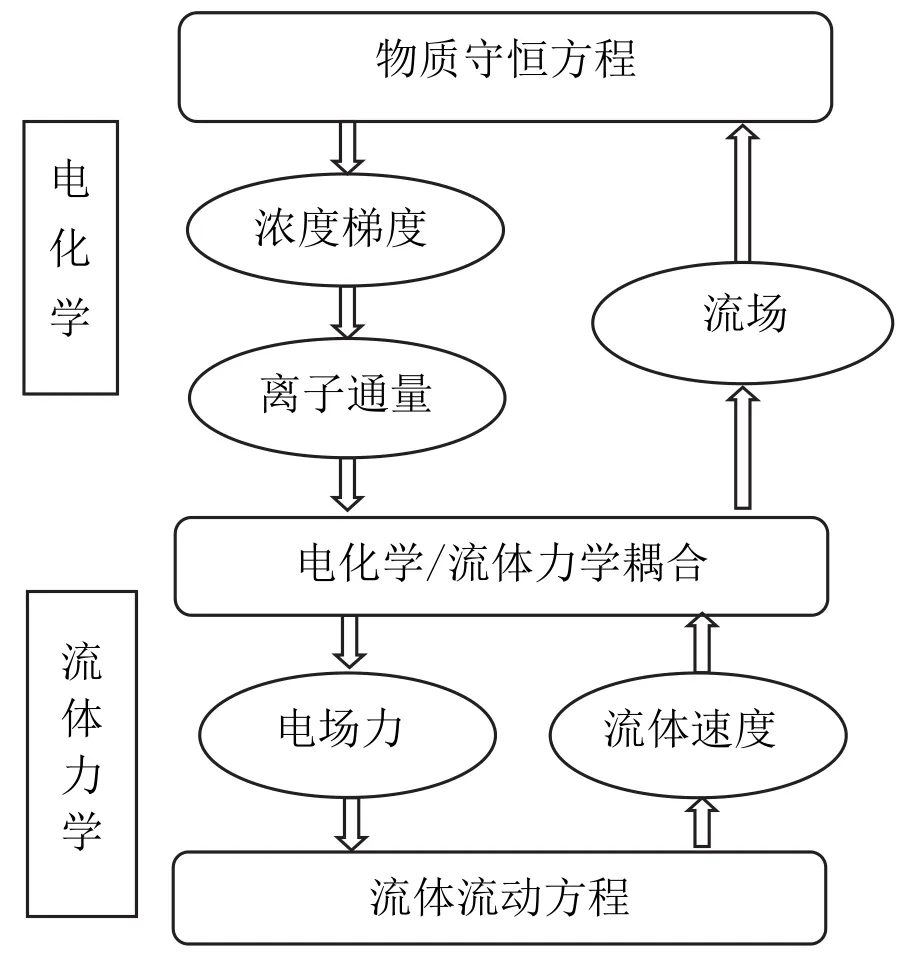
图2 电镀铜物理场之间的耦合关系Figure 2 Coupling relationship between physics fields in copper electrodeposition

电镀铜镀层厚度d的变化用法拉第定律描述：

电镀铜时，电极表面电流密度与离子通量N密切相关。离子通量变化由浓度梯度引起的离子扩散，电场作用下带电离子的迁移与镀液对流引起的离子传输三个因素决定。酸性镀铜液中的离子主要包括物质f的物质平衡方程用Nernst–Planck方程描述：

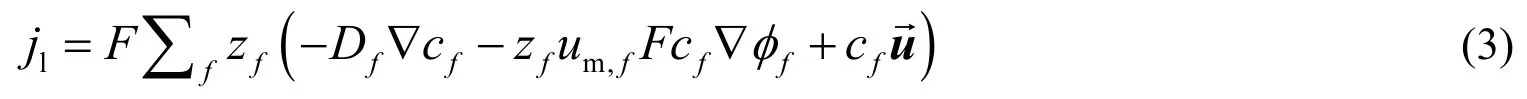
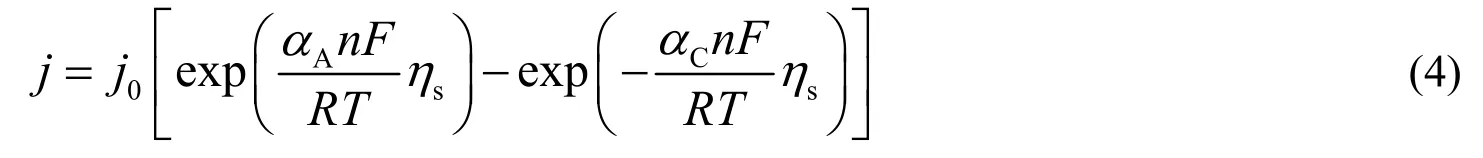
电极上存在浓度变化，向方程(4)引入修正项，得到：

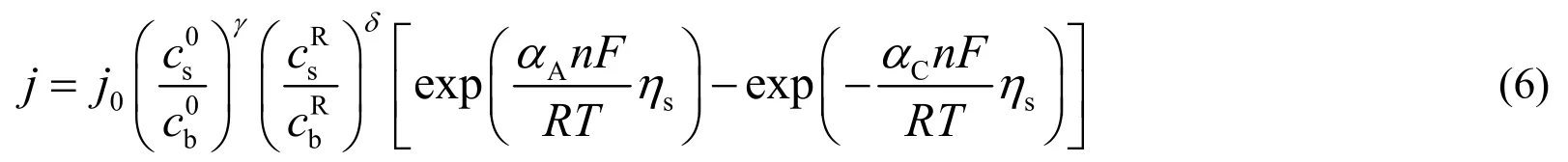
数值模拟时，非线性电镀体系的阴极电流与电势分布需要迭代求解，但边界条件中包含了未知源项，求解非线性体系的解析解需要进行线性化处理并对电化学体系进行近似[11-12]。电化学体系近似为一次电流分布、二次电流分布、传质控制与三次电流分布，其近似条件、控制方程与边界条件列于表1。

表1 电流分布近似条件Table 1 Approximation of current distribution

RDE电镀铜时，电极旋转引起槽内镀液流动，三次电流分布考虑了对流引起的铜离子浓度分布。电极旋转速度引起的流体流动用Navier–Stokes方程与连续性方程描述。

连续性方程与动量方程为：

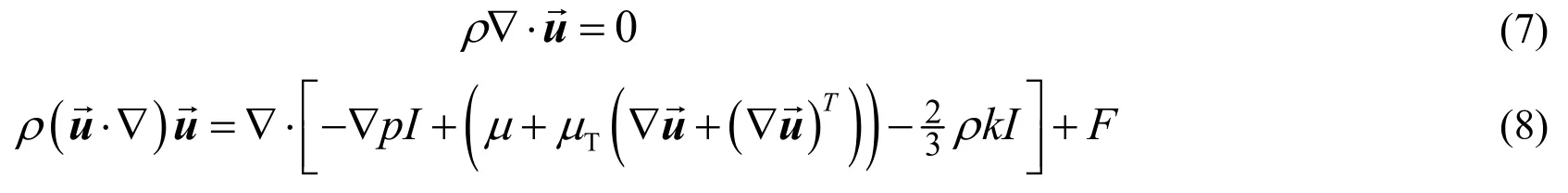
式中F表示体积力，计算时设置为零；p为压力，计算时设置为大气压。分别是镀液的动力学黏度与湍流黏度。湍流黏度为经验系数(取值0.09)，k为湍流动能，ε为湍流耗散率。

k与ε传输方程为：

RDE研究酸性镀铜液的电镀铜特征在Autolab电化学工作站与电解池中完成，数值模拟借助多物理场耦合软件Comsol Multiphysics完成，通过求解流体动力学方程和对流−扩散方程在稳态时的值进一步分析电极与溶液的相对运动，讨论电极表面流体流动对RDE电化学过程的传质影响。为了提高数值收敛性，采用两步进行计算。首先流体连续性方程与Navier–Stokes方程用于确定槽内流体的速度分布，随后将速度分量与物质瞬态传质方程耦合，考虑电迁移、对流与扩散引起的铜离子传输，用Nernst–Planck方程与Butler–Volmer方程得到不同旋转速度下电极附近铜离子浓度分布，结合法拉第定律求解不同尺寸直径的电极表面的电流密度分布以及对铜沉积的影响。

RDE电镀铜数值模拟步骤如下：

(1) 构建几何模型，如图3所示。RDE旋转轴作为z轴，磷铜圆盘作为对电极，置于电镀槽底部，与工作电极相对应。

(2) 设置控制方程与边界条件。流体运动方程用式(7)～(11)描述，物质传递与电极动力学方程用式(1)～(6)描述。为了提高数值收敛性，设置阳极电势为零，流体压力参考点压力为零。

(3) 划分计算域网格。RDE电镀铜模型网格如图4所示。在阴极表面建立边界层网格，最底层网格尺寸为500 nm，其余部位划分为自由三角形网格，将连续的计算域通过节点离散为子域，网格节点为求解物理量的几何位置。

(4) 采用迭代方法求解离域后的方程组并对模拟结果进行分析。计算域网格划分后，进行离散转化为代数方程组。方程组的结构化网格采用对角矩阵算法求解，非结构化网格采用迭代法提高数值收敛速度。数值模拟主要参数列于表2。

图3 RDE电镀铜数值模拟示意图Figure 3 Schematic diagram of numerical simulation for electroplating copper on RDE

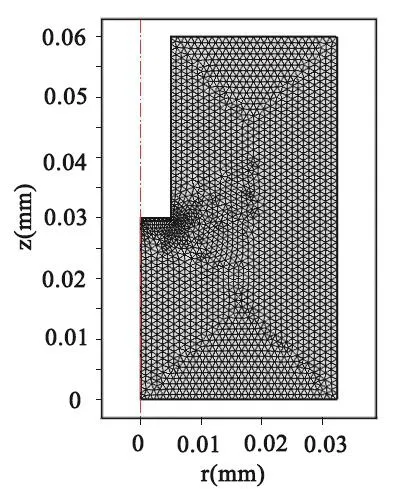
图4 RDE电镀铜模型计算域网格Figure 4 Computational grid for the RDE copper electroplating model

表2 电镀铜数值模拟参数Table 2 Parameters for numerical simulation of copper electrodeposition

2 结果与讨论

2. 1 镀液流场分布

电镀铜时，电解池内镀液对流方式，尤其是RDE表面镀液流动，会影响电极表面电流密度与镀层分布的均匀性。当RDE转速分别为500、1 200、2 000与3 000 r/min时，电解池内镀液流场分布如图5所示，其中箭头表示镀液流动方向。从中可以看出，当电极旋转时，与圆盘中心相接触的溶液在离心力的作用下向圆盘边缘运动，引起电极底部溶液向上流动并冲击圆盘中心，运动到与圆盘接近时，在离心力的作用下甩向圆盘边缘，形成了电解池内镀液的循环，引起涡流[13]。镀液流动的影响用雷诺数来表征。雷诺数的定义为：(其中为电镀液密度，为电极旋转角速度，为测量点与电极的距离，为电镀液黏度。当镀液流动速度较小时，雷诺数比较小(Re ＜2 000)，镀液流动方式为层流。随着RDE转速的增加，雷诺数增加，镀液流动从层流过渡为湍流。图5显示，当RDE转速小于1 200 r/min时，电解池内镀液流动为层流方式。随着RDE转速增加到2 000 r/min，电解池内逐渐形成多个涡流中心，此时镀液流动方式过渡为湍流。当RDE转速大于2 000 r/min时，镀液湍流引起电解池内更加复杂的镀液对流，进一步影响电解池内铜离子的传质和铜的沉积速率。

图5 RDE不同转速下电解池内的流场分布Figure 5 Flow field distribution at different rotating speed of RDE in electrolytic bath

当RDE以3 000 r/min旋转时，电解池内RDE附近镀液流动速度变化规律如图6所示。电极对称轴下方的镀液，即r为0 mm处，随z方向离开电极距离的增加，镀液流动速度加大。RDE中心处镀液的流动速度为零。电解池内距离RDE对称轴越远，镀液流动速度越大。对相同r处的镀液流动，其速度随离开电极的距离z的增加而趋向稳定，最后达到恒定值。在层流条件下，RDE旋转使其表面形成了一定厚度的流体边界层。电极旋转速度越大，被旋转圆盘所拖带的液层越薄，即流体边界层厚度越小[14]。在流体边界层内，存在液体的切向运动，通过扩散和对流实现铜离子的传质，形成一定的铜离子浓度分布特征。

2. 2 扩散层厚度分布

当RDE以一定的转速(400 ～ 6 000 r/min)旋转时，电解池内形成稳定的速度分布。电势阶跃到极限电流区引起了类似无对流时的暂态电流，并表现为一个稳态值，铜离子在电极表面附近形成稳定的浓度分布，如图7所示。在距离电极较远(＞80 μm)的镀液中，铜离子浓度为体浓度值(300 mol/m3)，随与电极距离的减小，电极表面铜离子的还原引起铜离子浓度降低，扩散层内形成一定的浓度梯度分布。RDE旋转速度越大，镀液中铜离子传质速度越快，电极表面铜离子浓度越高。当RDE转速为400 r/min时，电极表面铜离子浓度为290.5 mol/m3；当RDE转速增大为6 000 r/min时，电极表面铜离子浓度为297.5 mol/m3。

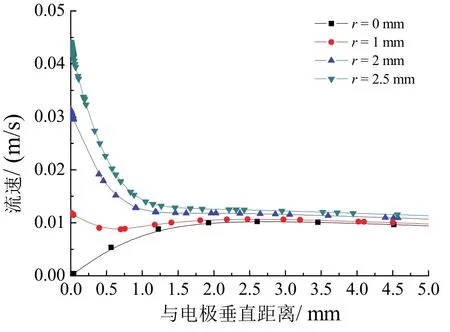
图6 3 000 r/min时RDE电极附近镀液流动速率的变化Figure 6 Variation of flow velocity of electrolyte near the RDE at 3 000 r/min

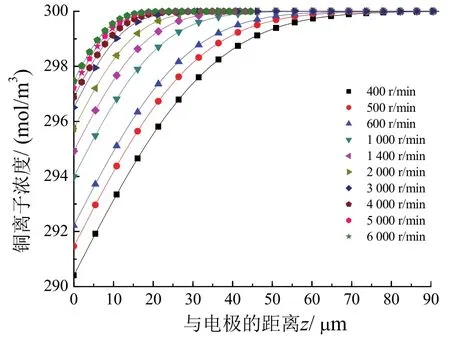
图7 在不同转速下RDE电极附近铜离子的浓度分布Figure 7 Concentration distribution of copper ions near the RDE at different rotating speeds

在一定转速下，RDE电极表面形成一定厚度的扩散层，铜离子通过扩散作用向电极表面传质并还原为铜，沉积在电极表面。扩散层厚度随RDE转速变化的曲线如图8所示。从图8可以看出，随RDE转速增加，扩散层厚度减小。当RDE转速较小(＜1 000 r/min)时，扩散层厚度较大，且随RDE转速的梯度变化明显。RDE转速为500 r/min时，扩散层厚度为33 μm；RDE转速为1 000 r/min时，扩散层厚度为23 μm。RDE转速超过1 000 r/min后，扩散层减小梯度趋缓。RDE转速为3 000 r/min时，扩散层厚度为13 μm；RDE转速增加到6 000 r/min时，扩散层厚度减小为9 μm。理论上，以RDE电沉积铜，扩散控制电极反应时，根据Levich方程，旋转圆盘电极表面扩散层厚度满足方程：据此对RDE不同转速下的扩散层厚度进行计算，获得扩散层的理论计算值，并与数值模拟结果进行对比，见图8。结果表明，多物理场耦合方法数值模拟得到的扩散层厚度与理论计算值吻合的很好，验证了数值模拟方法进行电镀铜研究的合理性。

图8 RDE不同转速下对应的扩散层厚度Figure 8 Diffusion layer thickness at different rotating speeds of RDE

2. 3 电流密度分布

电镀铜时，几何因素和电化学因素都会影响阴极表面的电流分布状况。旋转圆盘电极直径R分别为1、3和5 mm，电极转速为3 000 r/min时，电极表面一次、二次与三次电流分布特征如图9所示。

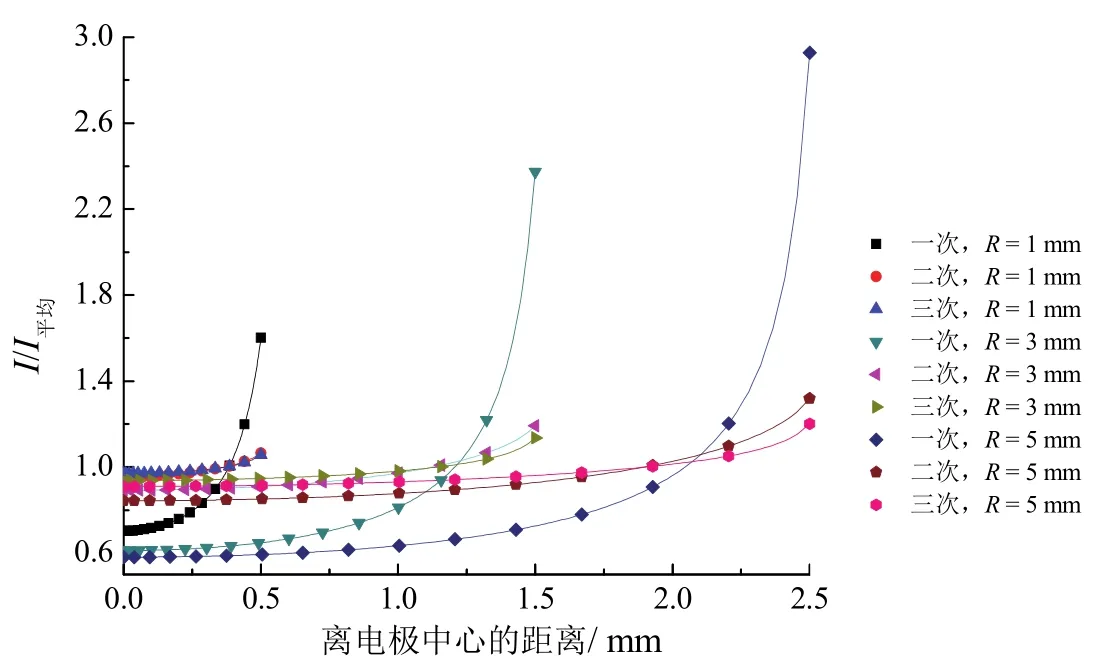
图9 RDE直径分别为1、3和5 mm时，电极表面的一次、二次与三次电流分布Figure 9 Primary, secondary and tertiary current distributions at electrode surface when the diameter of RDE is 1, 3 and 5 mm

从一次电流分布曲线可以看出，电极表面一次电流密度分布明显不均匀。由于一次电流分布仅考虑电解池几何形状对电场和电流分布的影响，而电极边缘处电场线分布密集离子流来自于边线和圆盘的垂直方向，使电极边缘处电流密度大于电极中心处电流密度，并且电极表面电流密度分布不均匀性随RDE直径的增加而加大。二次电流分布考虑了电极附近的电化学反应，电极极化使电极表面电流密度重新分配，二次电流分布比一次电流分布更均匀[16]。三次电流分布考虑了镀槽几何、质量传递、镀液导电性、铜离子浓度变化等因素的影响，图9显示其更为均匀。RDE电极直径越小，电极表面电流密度分布越均匀。因此，采用RDE研究电镀铜过程，宜使用直径较小的电极。

三次电流情况下，镀液流动会影响电极表面的电流分布状况。电极表面电流密度分布随电极转速的变化如图10所示。从图10可以看出，RDE转速影响电极表面的电流密度分布状况。随RDE转速的增加，电极表面电流密度趋于均匀分布，但在电极边缘处边界效应明显，电流密度急速增加。对于直径为3 mm的RDE电极，当转速从1 000 r/min改变为3 000 r/min，电极表面电流密度降低。电解池内镀液流动速度的加快，提高了铜离子的传质速率，消除了浓差极化，扩大了电流密度的范围。当RDE转速达到6 000 r/min时，电极表面电流密度均匀性提高，均一范围达到90%。对直径为5 mm的RDE电极分析也得到类似的结论：随着RDE转速的增加，电极表面电流密度分布趋于均匀，在6 000 r/min时均匀范围达到94%。因此，电化学研究流速对电极动力学反应的影响时，RDE较低的转速(100 r/min)用于描述镀液的静止状态，较高转速(＞1 000 r/min)可分析流速对铜沉积的影响。对于直径为1 mm的电极，当转速较小(＜1 000 r/min)时，电势和电流密度分布图像类似于球形电极表面电流密度分布特征[17]；在较高的转速(6 000 r/min)下，电极表面出现一段均一的电流密度分布区域，且离电极中心越远，电流密度越大。总之，RDE的使用提高了电化学反应速率，在较高转速下，电极表面电流密度分布均匀。RDE扩散层厚度可控的特征为电镀层均匀性的研究提供了手段。

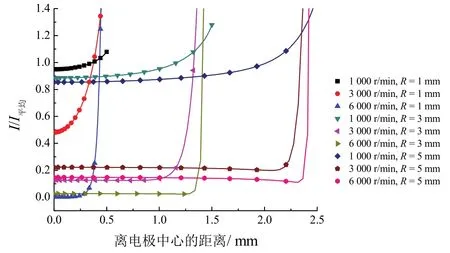
图10 RDE直径为1、3和5 mm时，电极表面三次电流分布随RDE转速的变化Figure 10 Variation of tertiary current distribution at electrode surface with RDE rotating speed when the diameter of RDE is 1, 3 and 5 mm

3 结论

采用多物理场耦合方法模拟了RDE的铜沉积过程，分析了RDE不同转速下电解池内的镀液流场分布、电极表面铜离子浓度分布、扩散层分布与电流密度分布的特征。结果表明，RDE转速会影响电解池内镀液的流动，在电极附近形成稳定的流体边界层和扩散层。在扩散层内，铜离子形成一定的浓度分布，模拟结果与Levich方程符合得较好。直径分别为1、3和5 mm的RDE电极表面的电流密度分布表明，RDE在高速旋转时，电极表面除边缘外电流密度分布均匀，电沉积时在电极表面可得到均匀的电镀层。直径1 mm的RDE电极表面的电流密度分布接近于球形电极的特征，而直径更大的电极表面的电流密度分布接近于平面电极的特征。RDE酸性镀铜数值模拟结果表明，多物理场耦方法能够较准确地对电镀体系进行预测和推理。此方法用于分析生产线电镀铜过程，有助于电镀铜工艺优化，帮助PCB生产商提高生产效率，降低成本，减少不良率。多场耦合方法对于指导电镀铜工艺及镀件镀层分布的均匀性具有借鉴意义。

[1] CHEN Y M, HE W, CHEN X M, et al. Plating uniformity of bottom-up copper pillars and patterns for IC substrates with additive-assisted electrodeposition [J]. Electrochimica Acta, 2014, 120: 293-301.

[2] VAN OLMEN J, HUYGHEBAERT C, COENEN J, et al. Integration challenges of copper through silicon via (TSV) metallization for 3D-stacked IC integration [J]. Microelectronic Engineering, 2011, 88 (5): 745-748.

[3] JI L X, WANG S X, WANG C, et al. Improved uniformity of conformal through-hole copper electrodeposition by revision of plating cell configuration [J]. Journal of the Electrochemical Society, 2015, 162 (12): D575-D583.

[4] JI L X, WANG C, WANG S X, et al. Multi-physics coupling aid uniformity improvement in pattern plating [J]. Circuit World, 2016, 42 (2): 69-76.

[5] TAO Z H, HE W, WANG S X, et al. Synergistic effect of different additives on microvia filling in an acidic copper plating solution [J]. Journal of the Electrochemical Society, 2016, 163 (8): D379-D384.

[6] BROEKMANN P, FLUEGEL A, EMNET C, et al. Classification of suppressor additives based on synergistic and antagonistic ensemble effects [J]. Electrochimica Acta, 2011, 56 (13): 4724-4734.

[7] TAKAHASHI K M, GROSS M E. Transport phenomena that control electroplated copper filling of submicron vias and trenches [J]. Journal of the Electrochemical Society, 1999, 146 (12): 4499-4503.

[8] ALEXIADIS A, CORNELL A, DUDUKOVIC M P. Comparison between CFD calculations of the flow in a rotating disk cell and the Cochran/Levich equations [J]. Journal of Electroanalytical Chemistry, 2012, 669: 55-66.

[9] DONG Q B, SANTHANAGOPALAN S, WHITE R E. A comparison of numerical solutions for the fluid motion generated by a rotating disk electrode [J]. Journal of the Electrochemical Society, 2008, 155 (9): B963-B968.

[10] JI L X, WANG C, WANG S X, et al. Multiphysics coupling simulation of RDE for PCB manufacturing [J]. Circuit World, 2015, 41 (1): 20-28.

[11] BOOVARAGAVAN V, BASHA C A. A novel approach for computing tertiary current distributions based on simplifying assumptions [J]. Journal of Applied Electrochemistry, 2006, 36 (7): 745-757.

[12] VOROTYNTSEV M A, KONEV D V. Primary and secondary distributions after a small-amplitude potential step at disk electrode coated with conducting film [J]. Electrochimica Acta, 2011, 56 (25): 9105-9112.

[13] VAZQUEZ-ARENAS J, PRITZKER M, FOWLER M. Kinetic and hydrodynamic implications of 1-D and 2-D models for copper electrodeposition under mixed kinetic-mass transfer control [J]. Electrochimica Acta, 2013, 89: 717-725.

[14] COLLI A N, BISANG J M. Validation of theory with experiments for local mass transfer at parallel plate electrodes under laminar flow conditions [J]. Journal of the Electrochemical Society, 2013, 160 (1): E5-E11.

[15] MISHCHENCHUK V V, NECHYPORUK V V, TKACHUK M M, et al. Mathematical modeling of nonequilibrium behavior of electrochemical systems with the electroreduction of anions [J]. Electrochimica Acta, 2013, 108: 153-166.

[16] KIM G S, MERCHANT T, D’URSO J, et al. Systematic study of surface chemistry and comprehensive two-dimensional tertiary current distribution model for copper electrochemical deposition [J]. Journal of the Electrochemical Society, 2006, 153 (11): C761-C772.

[17] DECONINCK J. Current distributions and electrode shape changes in electrochemical systems [M]. [S.l.]: Springer Science & Business Media, 2012.

[ 编辑：温靖邦 ]

Study of acidic copper electrodeposition using rotating disk electrode based on multi-physics coupling /

JI Lin-xian*, NIE He-xian, SU Shi-dong, CHEN Yuan-ming, HE Wei

A model for acidic copper electrodeposition on rotating disk electrode (RDE) was established based on multi-physics coupling method. The characteristics of flow field distribution and diffusion layer distribution at different rotating speeds of RDE in electrolytic bath were analyzed. The effects of rotating speed and size of RDE on distribution of current density and coating thickness were discussed. The results provide a theoretical guidance for the study of current density distribution and coating thickness uniformity on the electrodeposited object.

acidic coper electroplating; rotating disk electrode; multi-physics coupling; current density distribution; thickness uniformity; numerical stimulation

Yuncheng University, Yuncheng 044000, China

TQ153.14; TQ150.1

A文献标志码：：1004 – 227X (2017) 09 – 0437 – 08

10.19289/j.1004-227x.2017.09.001

2016–10–27

2017–04–15

运城学院院级项目（CY-2016005，YQ-2016016）。

冀林仙（1981–），女，山西平遥人，讲师，主要从事PCB工艺、电镀、仿真等方面的研究。

作者联系方式：(E-mail) jlxsxb@126.com。