基于“前测”，构建复习课

朱英英+戴银杏

【摘 要】“前测”是指教师在课前，通过不同的调查方式对学生进行相关知识预备和相关方法的预先测试，然后设计有针对性的教学活动，并提出相应的课堂教学策略。这对于复习课也是尤为重要的。本文以“平面图形面积的整理和复习”教学为例，教师可以通过“读懂前测，把握学情，有效复习梳理；基于前测，搭建支架，多向沟通求联；分析前测，抓住错例，着力突破难点；透过前测，关注差异，拓展提升求延”，最终实现小学数学复习课的有效构建。

【关键词】前测 复习课 有效构建 平面图形面积的整理和复习

“复习课”是小学数学课堂教学中的重要课型之一，在小学数学教学中占有重要的地位。复习课中，学生会对所学知识进行重建和再认，但更多的是对所学知识的重建、发现和顿悟，达到求联、求延、融会贯通，由此可见复习的重要。但是，在实际的课堂教学中，复习课成了许多教师惧怕、学生厌倦的一堂课。这种停留在“知识技能重现”层面的复习现状严重违背了复习的真正意图，与当前课堂教学改革格格不入。如何有效构建复习课堂，赋予复习课真正应有的生命力，是我们刻不容缓需要思考的问题。

基于“前测”下的小学数学复习课的有效构建改变了传统的复习整理模式，使教师明确了“复习什么”和“怎么复习”，赋予了复习课更深层次的教学内涵。下面，笔者试从以下几个方面展开探析。

一、读懂前测，把握学情，有效复习梳理

数学平面图形这一板块知识点多、杂、乱，而这些知识点又是分散在各个学段年级展开教学的。学生对这些知识点的识记、理解、运用到底在哪个程度呢？这些问题都需要教师掌握，这也是展开有效复习的前提。带着这些问题，笔者对天台外国语学校、临海大洋小学及三门六敖小学的两百余名学生展开了课堂前测。

【前测1】同学们，小学阶段我们学习了各种“平面图形的面积”。现在，请你回忆一下这些平面图形面积的计算公式和推导过程。然后用你自己喜欢的方式，如表格、图示、文字等，进行整理。通过整理，你有什么发现？

【前测分析】通过前测，我们发现三个学校的学生对于平面图形的面积掌握有一定的共同性，但是也有一些差异。大部分学生对于面积公式及推导过程掌握得比较扎实，对于转化思想有一定程度的体验。但是，通过前测，我们发现在学生头脑中的各平面图形面积之间的关系还是比较零散和单一的。学生知道图形之间有关系，但哪些图形之间存在关系？到底是怎样的关系呢？学生心中还不是特别清晰。

【复习对策】把握学情，有效梳理

课前在大屏幕上逐一展示学生对平面图形面积的整理作品。有列表格、画图、文字描述等。

师：通过整理，很多同学又有了新的发现，谁来说一说？

师：这些图形面积之间到底有什么联系呢？

同桌先讨论一下这些图形之间的联系，然后倒出信封里的六个基本图形在白纸上摆一摆、连一连，表示出它们之间的关系。

选择典型摆法的关系图黑板展示，并请学生逐一上台介绍。

师：比较这几张关系图，你有什么发现？

在没有进行前测时笔者和许多教师一样，把梳理点落在回忆各个图形面积公式的推导过程上，这已经没有必要。因为从学生的平面图形面积的整理作品中我们不难看出，学生对于各图形面积公式的来龙去脉和推导过程掌握得比较扎实。因此，在解读学生的作品后笔者调整梳理的方向，不重复展现各公式推导的不同方法，而是运用学生整理的公式，分析内在的联系，把重点放在图形关系的探究中。通过操作辨析，学生对平面图形的面积有了一个整体的认识，透彻理解“转化”就是沟通这些图形的桥梁。

可见，通过前测解读让教师看清并深入了解学生原有的认知状态和复习起点，摆脱以“自我为中心”分析教材、分析学生的思维定式，真正把“备学生”落到实处。站在学生认知基础上的复习活动，能更好地把握学生急需解决的问题，给学生创设一个主动而富有个性的自我梳理过程。通过展示学生的梳理作品，在欣赏和交流中潜移默化地渗透复习的整理方法和思路，切实提高学生的自主复习能力。

二、基于前测，搭建支架，多向沟通求联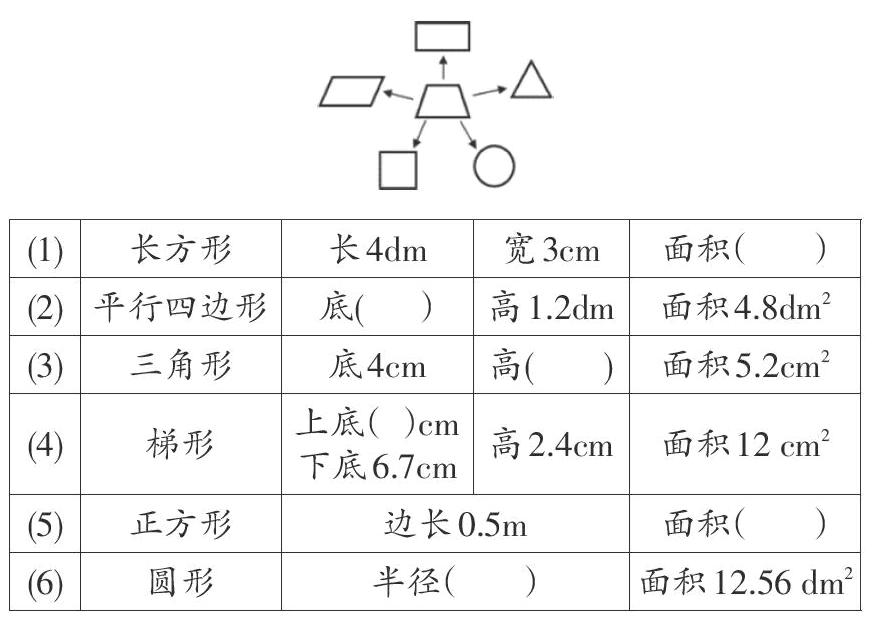

【前测1再解读】“抓住四基串成线，沟通联系连成片”是复习课的一个重要目标，本节课亦如此。通过学生的自主梳理、课堂反馈，学生已经基本把六个相对独立的平面图形再现、归纳、串联。但是，此时学生对平面图形面积关系结构的理解还是单一线性的，这是受教材编排的顺序所限制。通过对小学阶段学生需要学习的“图形与几何”知识的梳理，我们会发现教材在呈现相应的数学内容与思想方法时，是根据学生的年龄特征与知识积累，采用逐级递进、螺旋上升的原则进行编排的。学生在第一学段初步认识基本图形，三年级开始接触“面积”，学会第一个图形面积计算的就是长方形，在此基础上展开其他图形的面积学习，他们理所当然都认为所有的图形最后都一定会转化为长方形进行面积计算，这在学生对于平面图形面积的整理作品中都有所体现。这样的思维局限，显然限制了学生的发展。

【复习对策】搭建支架，多向求聯

在格子图中出示：你能根据图中信息补充画出哪些平面图形？并求出它的面积。

师：在脑中想象一下，然后把你想到的图形画出来，并求出它的面积。学生独立画图，并计算面积。

反馈各种图形：有三角形、长方形、正方形、平行四边形、梯形、圆形、半圆等。

师：同学们的空间想象力很好，画出了各种形状的图形。那么这些图形之间又有什么联系呢？

生：长方形和平行四边形等底等高，面积相等。

生：三角形面积和平行四边形等底等高，三角形面积是平行四边形面积的一半。

师：三角形要和这个平行四边形等面积，这个三角形可以怎么变？（等积变形）

师：如果在这组平行线之间画一个面积同为8cm2的梯形，又该怎样画呢？

生：只要上底+下底=8cm，就可以画出高是2cm、面积是8cm2的梯形。

生：这样的梯形能画无数个。

师：那现在我们就来看一下这些梯形之间的变化。（课件演示从梯形到长方形再到三角形的过程）

师：同学们，刚才除了看到梯形，你还看到了什么图形？（長方形，三角形）

师：当梯形怎样变化时，就变成了长方形呢？你会用梯形的面积公式来计算这个长方形的面积吗？

生：当梯形的上、下底相等时，就变成了长方形，（a+a）h÷2=ah=ab，S=ab就是长方形面积公式。

生：我认为三角形就是个上底或下底为0的特殊梯形，我可以这样算（a+0）h÷2=ah÷2，ah÷2就是三角形面积公式呀。

师：同学们，太棒了！现在请你们进行大胆的猜测，你觉得从梯形公式还能推导出哪些平面图形的面积公式呢？

在学生的猜测中，逐步给出新的图形面积关系结构图：

通过对底4为cm、高为2cm的图形进行想象，不断扩大图形的内涵，渗透图形之间的联系。再通过等积变形，给学生一个强大的思维刺激，引导他们发现“哦，图形之间原来还可以这样转化”。这种联系表现了特殊与一般的关系：对于一般梯形而言，三角形是个上底为0的特殊梯形，平行四边形就是个上下底相等的梯形。进而激发学生从更高的层次体验平面图形的内在联系、多向变换。

三、分析前测，抓住错例，着力突破难点

前测可以提供真实而全面的学生信息，可以了解学生原有知识水平中的一些共性特点，根据这些共性特点，教师在课中就可以抓住错例，有的放矢，对症下药，着眼调整复习重心，不再在每一个知识点上平均用力，而是将更多的时间花在认知难点上。

【前测分析】课前教师对每道题的正确率分别进行了统计。每一题的正确率如下：63%，96%，79%，86%，91%，90%。三个学校稍有差池，但无本质区别。学生通过六年的学习，计算公式的方法在脑海中深深地打下了烙印，因此对于平面图形的面积、高、底的计算是没有问题的。但是，错题出错的原因又何在呢？

【复习对策】抓住错例，突破难点

课中为学生呈现每道题的正确率，学生对于自己完成练习的结果非常关注。教师适时介入问题引发思考：第一题的正确率是63%，你觉得这37%的错误率原因在哪里？再看（3）（4）两题，正确率也不高。你们觉得错误的原因又是什么？

学生纷纷带着一种为班级同学排忧解难的激昂情绪自主陷入思考。

生：第一题要注意单位的统一。可以把4dm转换为40cm，也可以将3cm转换为0.3dm。

生：三角形的高应该是面积乘2再除以底。（教师课件演示）

……

师：比较一下，求三角形的高和求梯形的上底有什么相同之处呢？

在错题分析中打通三角形求高和梯形求上底之间的关系，突破难点。同时，根据前测学生对求三角形的高和求梯形的上底共性问题，展开重点探究。开放教学时空，为学生提供“发现、顿悟”的时间和空间。通过多媒体的有效演示，突破易错点、难点，充分调动了学生自主学习的积极性，激发了他们浓厚的探究兴趣，真正把解决问题的主动权交给了学生。

四、透过前测，关注差异，拓展提升求延

复习课中，教师对于复习材料总是“精挑细选”，尤其是习题方面，既怕太简单，成了枯燥的重复，又怕太难，学生看不懂、不会做。那么学生在统一的复习课堂中，如何在有限的四十分钟课堂中既能完成既定的复习巩固目标，又使每一名学生在自己的最近发展区有所发展、有所收获呢？我们需要借助“前测”。将传统的“教师出题”变为“学生荐题”，既能较好地反映学生原有的认知基础和能力水平，又能发现他们在认知、能力、水平、情感等方面的差异，从而针对差异设计练习教学，分层落实，满足需求，实现复习目标。

【前测3】

在学习平面图形的面积计算时，哪些题目容易出错呢？请你推荐一道题，整理如下：

推荐题目：

推荐理由：

我的解答：

【前测分析】在推荐易错题中，学生为了完成任务就会主动去思考“我需要为同学推荐什么样的易错题呢？”在无形之中，很多学生对自己曾经接触到的所有图形面积计算的题目进行了快速筛选，而且会主动去寻找一些易错题和难题先自己进行研究，因为只有这样，他才能合理地写出相关的推荐理由。可以说课中呈现了一些题目，其实它的背后支撑的是一批题目。从推荐题中可以看出学生之间存在较大差异。

【复习对策】关注差异，拓展求延

教师课前对学生推荐的易错难题进行分类整理，把这些题目按难易程度进行星级排队。课中分层展示，让学生进行挑战。学生跃跃欲试，积极性充分激发。

通过学生推荐易错难题，不仅能真实了解学生的知识储备，还能了解学生的思考方法和过程，当然更明确了学生对来自教师帮助的需要程度。前测，让不同层次的学生都得到展示，受到关注，既照顾了优秀学生“吃不饱”的现象，又解决了一般学生“吃不了”的问题，同时在多个层面的思考、碰撞中，能有序获得思维的不同程度的提升，使每一名学生都能发挥其最佳水平。教师基于前测，关注差异，才能有效引导学生拓展求延，实现数学能力的有效提升。

前测，提高了“复”的效率，提升了“习”的品质。让“复习什么”更贴近学生实际，“怎么复习”更符合学生的需要。因为前测，我们能准确制定符合学生实际的复习目标和确立复习重难点，有针对性地设计复习预案；因为前测，我们能有效地把握学生的思维起点和活动过程，有效地预设生成，把控课堂；因为前测，我们更能关注学生的差异，真正让复习课在梳理求联、拓展求延中有效构建。

参考文献：

[1]孙立勇.小学数学前测性学习的研究[J].基础教育，2014，（5）.

[2]孙建平.学情前测在数学课堂教学中的应用例谈[J].学生之友（小学版），2013，（3）.

（ 浙江省天台县天台小学 317200）