梯形测试题
盛东卫
一、填空题(每题3分,共27分)
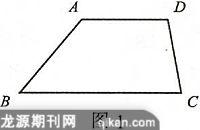
1. 如图1,梯形ABCD中,AD∥BC.若∠B=50°,∠C=80°,则∠D=_______,∠A=_______.
2. 梯形ABCD中,AD∥BC.若∠B=60°,AC⊥AB,那么∠DAC=_______.
3. 有一个直角梯形零件ABCD,AD∥BC,斜腰DC的长为10 cm,∠D=120°,则该零件另一腰的长是_______cm.
4. 已知等腰梯形的一个底角为60°,它的两底分别为13 cm和37 cm,则它的周长是_______.
5. 如图2,等腰梯形ABCD中,AD∥BC,AD=5,AB=6,BC=8,且DE∥AB,则△DEC的周长是_______.
6. 如图3,梯形ABCD中,AD∥BC,AD=AB=DC,BD⊥DC,则∠C=_______.
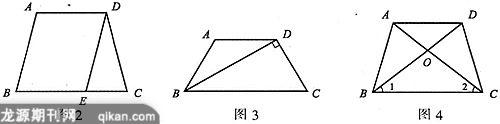
7. 如图4,梯形ABCD中,AD∥BC,对角线AC、BD交于点O.分别添加如下条件:①AC=BD;②OA=OD;③∠1=∠2;④OA=OC.其中能使梯形ABCD为等腰梯形的有_______(填序号).
8. 已知等腰梯形的两条对角线互相垂直,高为6 cm,则此等腰梯形两底的和是_______cm.
9. 如图5,等腰梯形ABCD中,AB=AD=DC=1,∠ABC=60°.P是过上、下底中点E、F的直线上的一点,则PA+PB的最小值为_______.
二、选择题(每题3分,共27分)
10. 四边形ABCD中,∠A∶∠B∶∠C∶∠D=3∶3∶1∶5,则这个四边形是().
A. 对边不平行的四边形 B. 等腰梯形
C. 直角梯形 D. 平行四边形
11. 下列命题错误的是().
A. 等腰梯形是轴对称图形
B. 等腰梯形的两条对角线相等
C. 等腰梯形在同一底上的两个角相等
D. 等腰梯形的两底平行且相等
12. 四边形ABCD中,AD∥BC,AC=BD,则四边形ABCD是().
A. 平行四边形 B. 等腰梯形 C. 矩形 D. 等腰梯形或矩形
13. 梯形的两底分别为16 cm和8 cm,同一底边上的两个角分别为60°和30°,则较短的腰长为().
A. 4 cm B. 8 cm C. 6 cm D. 12 cm

14. 如图6,若梯形ABCD的对角线交于点O,则图中共有面积相等的三角形().
A. 1对B. 2对C. 3对D. 4对
15. 下列结论中,正确的是().
A. 有一组邻角相等的梯形是等腰梯形
B. 只有两个角相等的梯形是等腰梯形
C. 有一组对角互补的梯形是等腰梯形
D. 有两组角分别相等的四边形是等腰梯形
16. 如图7,D、E、F分别是△ABC各边的中点,AH是高.如果ED=5 cm,那么HF的长为().
A. 5 cmB. 6 cmC. 4 cmD. 不能确定
17. 如图8,在梯形ABCD中,AB∥DC,E、F、G、H分别是各边的中点.要使四边形EFGH一定是矩形,则下列补充的条件中正确的是().
A. AC⊥BD B. AC=BD
C. AD=BC D. ∠BCD=∠ADC
18. 在下列图形中,沿着虚线将长方形剪成两部分,那么由这两部分既能拼成三角形,又能拼成平行四边形或梯形的是().

三、解答题
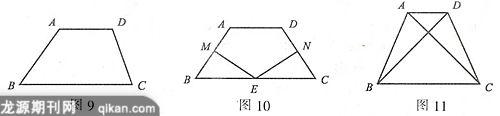
19. (11分)如图9,梯形ABCD中,AD∥BC,AD=8,BC=17,∠C=70°,∠B=55°.求DC的长.
20. (10分)如图10,在等腰梯形ABCD中,AD∥BC,AB=DC.点E是BC边的中点,EM⊥AB,EN⊥CD,垂足分别为M、N.求证:EM=EN.
21. (15分)如图11,梯形ABCD中,AD∥BC,AB=DC,AC⊥BD.若AD=4,BC=10,求梯形ABCD的面积.
22. (15分)已知梯形ABCD,其中AB∥CD,现添加一个条件,例如AD=BC,可使梯形ABCD是等腰梯形.那么除了AD=BC外,还可以添加一个什么条件,能使梯形ABCD是等腰梯形?甲、乙、丙、丁四位同学分别添加了一个条件.

甲:∠A=∠B;乙:∠B+∠D=180°;丙:∠A=∠D;丁:梯形是轴对称图形.
(1)你认为哪些同学的条件符合要求?请说明理由.
(2)你能添加一个其他的条件,使梯形ABCD是等腰梯形吗?
23. (15分)如图12,△ABC中,∠ACB=90°,E、F分别是AB、AC的中点.D是BC延长线上一点,且CD=1/2BC.试判断四边形EBDF的形状,并证明.
四、拓展题
24. 如图13,已知直角梯形ABCD中,AD∥BC,AB⊥BC,AD+BC=AB,点O是CD的中点.连接OA、OB,试判断△AOB的形状,并证明.
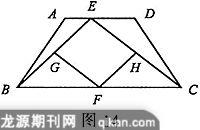
25. 如图14,等腰梯形ABCD中,AD∥BC,点E是线段AD上的一个动点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.
(1)试判断四边形EGFH的形状,并说明理由.
(2)当点E运动到什么位置时,四边形EGFH是菱形?
(3)若(2)中的菱形EGFH是正方形,请猜想线段EF与线段BC的关系,并证明你的猜想.
- 中学生数理化·八年级数学人教版的其它文章
- 废墟上的花朵
- 消点法的运用(一)
- 四边形的“一般与特殊”,“性质与判定”
- 多角度地深化四边形的知识
- 四边形知识解读
- 期中复习导航

