旋转变换巧解题

◇刘 琨

某地区小学生毕业质量检测试卷中有一道填空题：如图1，直角三角形ABC是由甲、乙两个小三角形和一个正方形拼成的。已知AD=2.2厘米，BD=4.1厘米，那么∠1+∠2=（ ）°，甲+乙=（ ）平方厘米。

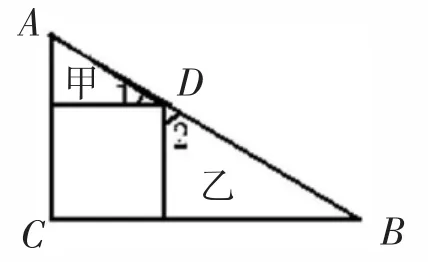
图1

阅卷结果显示，近500名学生中，求“∠1+∠2=（ ）°”的正确率高达90%；而求“甲+乙=（ ）平方厘米”的正确率不足20%。求组合图形的面积，教材上一般采用分、合的方法，已经在学生的大脑里形成思维定式，并固化下来。

此题要求学生克服原有解题经验、思维习惯的干扰，寻找一种全新的解题思路。教学中可以这样引导学生思考：图中“正方形”在这里有什么作用？“∠1+∠2=（90）°”有什么作用？三角形甲和三角形乙又有什么联系？按照这种思考路径探索下去，不难发现，三角形甲和三角形乙有一条直角边相等，都是正方形的一条边，三角形甲和三角形乙又有同一个顶点D，再因为∠1+∠2=（90）°，因此，只要将三角形甲绕点D逆时针旋转90°（如图2），或将三角形乙绕点D顺时针旋转90°（如图 3），这样，通过旋转变换，就可以巧妙地将甲、乙两个看似孤立的三角形组合成一个新直角三角形，变化后边AD和边BD分别成了直角三角形的两条直角边。到这里，问题便可迎刃而解。

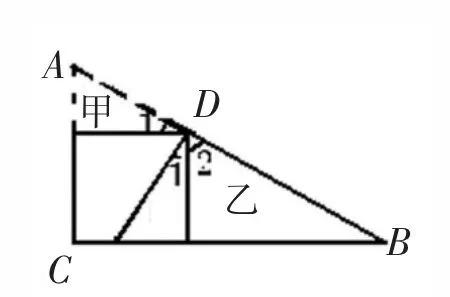
图2

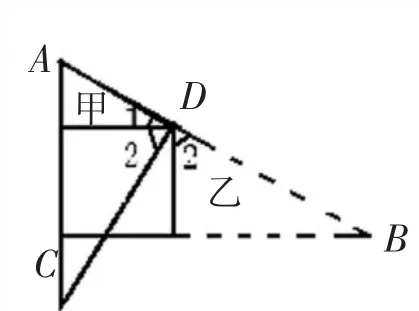
图3

教学中，教师要注重培养学生敢于猜想、善于探索的思维品质，给学生创造宽松、开放的教学环境，鼓励学生大胆猜想、小心验证，使学生的思维更加开阔，思路更加灵活。