“由此，我们自然地想到……”——谈数学教学中的“施”法自然

◇张 霞

上初中的女儿上完学校的数学兴趣课回来，兴奋地在我耳边念叨辅导老师的一句口头禅 “由此，我们自然地想到……”，多少看起来让人摸不着头脑的数学难题就在这一步步“自然地想到”中悄然化解，同时化解的还有女儿心中对数学难题的诸多焦虑。

恰逢基层调研听随堂课，一节二年级的数学练习课让我感慨颇多：教师善于思考，书本上的习题被有效地调整、组合、拓展；学生乖巧，努力地听、努力地想，只是常常两眼迷惘，有劲儿使不上。教的“齿轮”与学的“齿轮”不能咬合，原因何在？

两事相联，我感觉，我们的数学教学还需多一些“施”法自然。

一、表达想法，自然比追求精准更重要

师：如图1，怎么想到商7的呢？

图1

生：因为43很接近7个6。

师：很接近7个6，也就是什么？

生：43里面有7个6。

师追问：43里面有7个6还可以怎么说？

众生沉默片刻，一生举手试探：43里面最多有 7个 6。

师：真好，我们在想商时，需要思考的是一个数里面最多有几个几。

数学教师追求数学表达的精准是其责任心的体现，但这精准应是两把尺子，严以律己而宽以待生。正如吴正宪老师所强调的“严格的不理解不如不严格的理解”。如果一开始就要求学生精准表达，会让学生不知问题所指，茫然不知所措。个别学生通过模仿教师的表述以迎合，但并不能表明他们真的理解，或许只是鹦鹉学舌，得其表而失其里；受挫的大部分学生，却会失去说真话的勇气及能力。学生表达自己的想法，贵在真实、自然、率性。事实上，真正的理解常常表现为用自己的方式表达出来。当学生的表达有失偏颇时，教师可以通过题型的变化让学生慢慢领悟。如上面的教学中就可以出题：44÷9=？追问学生：“为什么商不是5呢？五九四十五，45不是更接近44吗？”在追问中使学生明晰，虽然45最接近44，但它超过了44，说明44里面不够5个9，最多只有4个9。

二、数学思考，自然发散比被动前行要有趣

师：如果☆÷6＝□……○，那么，○最大是多少？

生：最大是5。

师：如果☆÷○＝□……6，那么○最小是多少？

生：最小是7。

师：在☆÷7＝□……6中，如果商是4，☆是多少？

众生沉默，一段时间后一只小手举起，答：4×7＝28，28＋6=34，☆是 34。

师追问：4×7求的是什么？

学生支吾不能答。

师：求的是 4个 7分掉了 28，还余下 6，所以加上6就是被除数了。

师：在☆÷7＝□……6中，如果商是5，☆又是多少？

半数学生举手：5×7＝35，35＋6=41，被除数是41。

此教学片段意在用题组的变化，加深学生对“余数须比除数小”的理解，并了解到被除数、除数、商、余数四者之间的关系，学会借助它们间的关系求出被除数。但是在执教过程中，随着题型越变越多，能够应付教师提问的学生越来越少。根据皮亚杰的认知发展理论，二年级的学生尚处于具体运算阶段的前期，类似“☆÷6＝□……○、☆÷○＝□……6、☆÷7＝□……6”的问题相对抽象，让他们不经纸笔协助而仅凭心智的抽象运算立刻口答出结果，是相当吃力的。二年级学生的注意力水平决定了他们不可能仅凭借乖巧长时间地关注并深入思考抽象且枯燥的题目。

与其按照教师的“序”走得磕磕绊绊，还不如指明方向，让学生的思维自然发散拓展，再梳理感悟。如在练习“☆÷6＝□……○，○最大是多少”之后，提出：“像这样的题目还可以怎么出？”模仿出题对学生来说并非难事，又恰好符合学生爱想象、爱探索、爱创造的天性，是件让他们振奋的事情。在学生展示、评析、筛选后，教师追问：“怎么一会儿求‘最小’，一会儿又求‘最大’呢？”点出变化的关键之处——因为余数要比除数小，所以知道除数求余数，必是最大；知道余数求除数，必是最小。顺势拓展：“在‘☆÷7＝6……□’中，可以求最大的被除数还是最小的被除数呢？为什么？”最后回顾梳理，体验“余数须比除数小”这一小小知识点考查方式的变化多样。

三、规律掌握，自由运用比先导后演更有效

师：看课本第7页的思考题：□÷□＝□……3，这时除数最小是多少？

生 1：最小是 2。

生 2：最小是 4。

师追问：为什么是4而不能是2？

生3：除数必须比余数大而不是小。

师：如果除数是4，你能写出一个算式吗？

生自做，师巡视，强调：写出一个算式后便可以举手。

师讲评：□÷4＝□……3，商可以是多少？如果商是1，被除数是多少？

生：被除数是7。

师：商还可以是多少？

……

此教学片段意在引导学生领会“依据‘余数须比除数小’，先确定最小的除数，再定商来求被除数”的解题思路。一步一步，紧牵学生的手。学生就像久居瓶中，因瓶盖拧紧、失去蹦跳空间而慢慢丧失蹦跳勇气和能力的跳蚤。

其实，“乱”一点儿又何妨？请看如下教学片段：

师：孩子们，这是一道思考题，不过，相信难不倒大家，大家可以试着写几个算式。

1.可以在“乱”中诊断，加深认识。

师：孩子们，这是大家创造的几个算式，你们看如何？

展示学生的作品：18÷5＝3……3；19÷4＝4……3；11÷2＝4……3；27÷6＝4……3。让学生在辨析中明确：因为余数要比除数小，所以除数最小只能是4，其中 11÷2＝4……3 是错误的创造。

2.可以在“乱”中理序，领悟做题技巧。

师：孩子们，除数最小是4，那么像 19÷4＝4……3这样除数是4的算式还有哪些？

展示学生的作品：39÷4＝9……3；15÷4＝3……3；27÷4＝6……3；35÷4＝8……3；23÷4＝5……3。

师：如果给这些算式排序，你觉得可以怎样排呢？

展示：

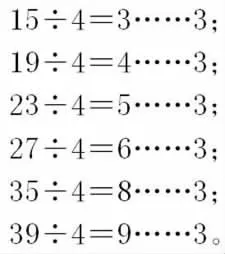
师：想一想，除数是4的算式是不是只有这些？如果不是，还有哪些呢？你是怎样想到的？

3.可以在“序”中拓展，提炼解题之道。

问题1：除数最小是4，还可以是哪些数？

问题 2：如果除数是5，在□÷5＝□……3中，你又能写出哪些不同的算式？能写出几个呢？

问题3：你觉得怎样想可以又对又快？

思维不能带着镣铐跳舞，与其给予现成的解题序列，不如遵循自然，由乱开始，放手让学生自由想。在思维热身后回头再看；在回头看中辨别是非，明晰关键；汇集学生自然生成的材料，乱中理序，序中查漏，提炼方法，领悟内涵。

总之，数学教学中的“施”法自然，实质上就是放下教者自身的序，关注学习者自然生成的“序”，在此基础上设法引导，以学定教。