高考数列中不等式的证明

贵州省遵义市正安县格林镇永长村校(563405)

叶 飞●



高考数列中不等式的证明

贵州省遵义市正安县格林镇永长村校(563405)

叶 飞●

对数列的考查，是高中数学的难点，也是高考的热点.一般解法是利用重要不等式，对不等式进行放缩，并结合数学归纳法进行证明.本文结合高考题，对数列不等式的证明进行讨论.

不等式;数列；数学归纳法；放缩法

数学归纳法是用来证明某些与自然数有关的数学命题的一种推理方法，在解数学题中有广泛的应用，尤其在数列的相关证明中发挥重要的作用.

分析 该题的两道小题均涉及对一切正整数均成立的问题，从而优先考虑数学归纳法，

解 (1) 用数学归纳法.先证明a2为奇数.

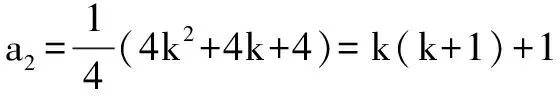
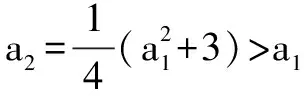
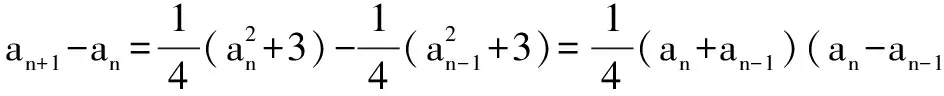
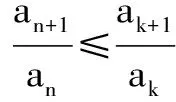
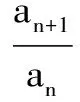
解 (1)a2=2λ+λ2+2(2-λ)=λ2+22,

a3=λ(λ2+22)+λ3+(2-λ)×22=2λ3+23,

a4=λ(2λ3+23)+λ4+(2-λ)×23=3λ4+24.

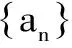
a.当n=1时，a1=(1-1)λ+2=2,等式成立.

b.假设当n=k时成立，即ak=(k-1)λk+2k，则有

ak+1=λ[(k-1)λk+2k]+λk+1+(2-λ)2k=kλk+1+2k+1,

从而当n=k+1时，等式成立.

因此，an=(n-1)λn+2n对任意n∈N*均成立.

(2) 设bn=(n-1)λn，则bn的前n项和

Tn=λ2+2λ3+…+(n-2)λn-1+(n-1)λn，

λTn=λ3+2λ4+…+(n-2)λn+(n-1)λn+1.

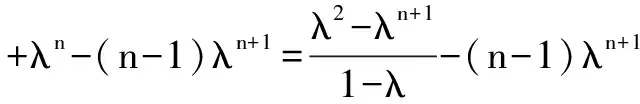
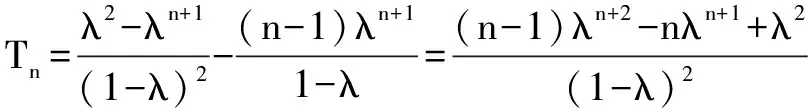
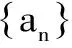
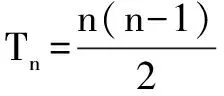
因为λ>0，所以an>0，要使得不等式成立，只要2an+1<(λ2+4)an(n≥2).

而(λ2+4)an=(λ2+4)(n-1)λn+(λ2+4)2n>4λ(n-1)λn+2n+2≥2nλn+1+2n+2=2an+1,n≥2,

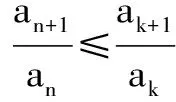
小结 从上面两个例子可以看到，对于数列中的不等式进行处理，首先根据前几项发现一般规律，再使用数学归纳法进行证明，并结合重要不等式，这是一种常用的处理手段，也是高考数学中考查分析能力的一种重要方法.

[1]刘剑鹏. 高中数学中数列的解题技巧探析[J] . 数理化解题研究.2016，28：39

[2] 文卫星. 挑战高考数学压轴题[M].上海：华东师范大学出版社,2010

[3] 曲一线.五年高考三年模拟[M].北京：首都师范大学出版社,2016

G632

B

1008-0333(2017)13-0039-01