高中数学中基于函数问题的教学策略分析

江苏省苏州市昆山市第一中学 周维军

高中数学中基于函数问题的教学策略分析

江苏省苏州市昆山市第一中学 周维军

作为高中数学的主要组成部分，函数是很多数学题目的解题关键，同时也是学习其他数学知识的基础。函数知识内容较深，学生学习的难度较大，需要较长的时间才能掌握。为了让学生更好地掌握函数知识，教师应该在教学过程中充分认识函数的重要作用。本篇文中笔者在高中函数知识的基础上深入研究函数知识教学，以此推动高中函数教学的发展。

高中数学；函数教学；教学策略

函数知识是高中数学教学中的难点重点，贯穿于整个高中数学教学过程中。有关函数知识的考题也是历年高考的重点题型，且函数非常灵活，变化很多。高中数学教师应该根据新教材中有关函数知识的变动，深入挖掘教材，精确定位函数知识的重点难点，结合其他数学知识和考点进行教学，以保持教学与课程标准同步，使学生充分理解函数知识的本质。

一、函数概念教学方式

函数概念是高中数学函数的基础内容，是学习其他函数知识的前提，所以教师应该在函数教学过程中重视函数概念的教学。换句话说，学习函数概念的作用就是让学生明白“函数是什么”的问题。在教授函数概念的过程中，高中数学教师先让学生预习课本，然后总结出有关函数概念的疑问，要让学生明白函数作为一种数学模型，主要用于刻画两个变量之间的关系，函数的本质是一种对应，对应法则f可以是一个数学表达式，也可以是一个图形或是一个表格，对应是建立在A﹑B两个非空的数集之间，可以是有限集，当然也可以是单元集，如f（x）=2x（x≠0）。在课堂上，教师再根据学生提出的疑问进行讲解分析，教师讲解完之后，让学生课后总结和运用所学到的函数基础概念知识进行练习，为学生今后学习更高级﹑更复杂的函数知识打好基础。因为函数概念的复杂性，教师应该循序渐进地展开函数概念教学，不能急于求成。比如学生对于复合函数的概念很难理解，如果教师一来就给出一些题目让学生做，一道道题目计算下来，并不一定能帮助学生理解函数概念，反而会令学生对函数概念更加模糊。比如下面这道题：

案例1：求下列各题中的函数f（x）的解析式。

（1）已知f（1-x）=2x2-x+1，求f（x）；

分析：此题学生拿了会不知道如何下手，教师可从已知函数f（x）=x+3，求f（0），f（3），f（t），f（t+1）的值出发，由浅入深，揭示复合函数的本质，再利用换元法或凑配法解决问题。

解析：（1）（换元法）设t=1-x，则x=1-t，

∴f（t）=2（1-t）2-（1-t）+1=2t2-3t+2，

∴f（x）=2x2-3x+2。

∴f（x）=x2+2。

∴f（t）=（t-2）2+4（t-2）=t2-4，

∴f（x）=x2-4（x≥2）。

∴f（x）=x2-4（x≥2）。

教师在实际教学中给出的题目之间应该是有联系的，注重解题的过程，应该先讲解函数概念再安排学习做题，在解题的过程中引导学生进一步加深对函数概念的理解。如果是先做题，即便是所有题目学生都做对了，也很可能知其然不知其所以然。教师应该让学生理解题目之间的关系，逐步让学生明白为什么会出这样的题目，并且通过比较找出题目之间的区别和联系。如此一来，学生就很容易理解函数概念，进而运用函数概念帮助解题。

二、函数单调性教学策略

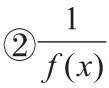
案例2：已知函数y=log2（ax-1）在（1，2）上单调递增，则a的取值范围为________。

分析：此题为典型的一次函数和对数函数的复合函数形式，注意到对数函数的底数为2，故只需要一次函数也为单调递增函数即可，同时需注意真数要大于零。

解析：令m=ax-1，则函数y=log2（ax-1）在（1，2）上单调递增等价于m=ax-1在（1，2）上单调递增，且ax-1＞0在（1，2）上恒成立，即a＞0，a-1＞0，即a＞1。

三、函数奇偶性和周期性教学设计

函数的奇偶性和周期性都是从函数图象抽象出来的特殊性质，函数图象具有对称性，通常具有奇偶性，可用多媒体展示日常生活中常见的对称现象，如美丽的蝴蝶﹑太极八卦图等等，并让学生自己列举生活中对称的实例，从而抽象刻画出一类特殊的对称性——奇偶性。

分析：首先让学生分别计算x=±1，x=±2，x=±3时的函数值，通过特殊值让学生发现两个函数的对称性反映到函数值上具有的特性：，进而提出在定义域内是否对所有的x都有类似的情况？借助课件演示函数的图象，学生通过观察和运算发现两个函数具有上述不同特性，即两个函数各自对称性的实质是：自变量互为相反数时，函数值相等和互为相反数这两种关系，然后通过解析式给出严格证明，进一步说明这两个特性对定义域内任意的一个x都成立。

通过探索奇偶性定义的过程，使学生关注函数奇偶性与函数对称性的关系，并体会数形结合﹑猜想归纳的数学思想。

在一定范围内函数呈现规律性变化，一个完整的变化规律就是函数的变化周期。三角函数是函数周期性性质的典型代表，比如正弦函数和余弦函数。而且不仅在数学中周期性很重要，在现实生活中周期性也经常用来描述现实生活中的重复规律，如我们可以用周期性来描述有周期性变化的量与量之间的关系，因此非常有必要让学生掌握函数的周期性。比如正弦函数的周期是2π，余弦函数的周期也是2π，这两个三角函数的函数周期性是完全一样的，高中数学中关于三角函数的内容比较多，也是高考中的必考点。三角函数的实用性非常强，因此教师在教学中可以用三角函数来举例讲解函数的周期性，但是很多教师仅仅是给学生展示一些正弦或余弦函数的图象，然后再根据sin（x+2kπ）=sinx（k∈z）让学生观察函数值重复出现的图象规律，从而引出函数周期性的概念，最后让学生课外练习的都是三角函数的相关题目。这明显是错误的教学方法，教师应该在确定学生明白三角函数具有周期性的前提下，继续向学生提问：请大家列举出其他的具有周期性的函数。不管学生是否能答的上来，在提问之后继续向学生提出类似“f（x）=cosx，x∈[0，8]这个函数是否有周期性”这样的问题，通过这样的问题让学生认识到并不是所有的三角函数都有周期性。

综上所述，教师能否有效地教是决定高中函数教学效果的主要因素，作为引领学生学习的人，教师应该借助多媒体﹑实体数学模型﹑数形结合法等教学方式由浅入深﹑循序渐进地向学生讲解函数知识，帮助学生克服学习遇到的困难和畏难情绪。通过在教学方式上加以创新，帮助学生掌握函数概念，学会运用函数知识解决数学问题，只有教师用心教，学生用心学，才能让学生顺利地掌握高中数学函数知识。

[1]汤勇，修建伟.高中数学问题解决教学研究——以函数教学为例[J].中学课程辅导（教师教育），2015.

[2]顾国华.高中数学教学中函数的设计思路及其教学策略分析[J].数理化学习，2014.

[3]赵毅菊.高中函数教学研究[D].内蒙古师范大学，2008.

book=26,ebook=28