基于零漂修正和偏置补偿的定子磁链观测算法

卢亨宇，刘彦呈，郭昊昊，程世超

(1.大连海事大学，大连 116026；2.国网辽宁省电力有限公司大连供电公司，大连 116085)

0 引 言

永磁同步电机凭借其功率密度高、效率高、控制性能优良等优点得到了广泛应用。高效的控制策略需要获取精确的转子位置和速度信息，这些信息一般通过光电编码器等传感器获取。传感器的使用提高了电机控制成本，增加维护难度，降低了系统的可靠性。因此，国内外学者对永磁同步电机的无位置传感器控制进行了深入的研究。

永磁同步电机无位置传感器控制，根据其适用的转速范围，可分为两类：一类是适用于中低速的高频注入法，通过电机凸极效应对转子位置进行估算。这类方法在中低速的估算精度高，随着转速升高，基频信号与高频注入信号之间的频率越来越接近，导致滤波器难以提取位置信息，估算效果变差，并且此方法不适用于凸极率低的表贴式永磁同步电机。另一类是适用于中高速，基于电机模型的算法，通过计算反电动势或磁链来求得转子位置信息，主要包括：扩展卡尔曼滤波法、模型参考自适应法、滑模观测器，反电动势积分法等算法，其中反电动势法结构简单，易于实现，但反电动势积分法采用了电压积分模型，积分环节会受到积分初值和电压电流偏置的影响产生漂移。为了解决电压积分模型积分环节带来的问题，通常用一阶低通滤波器代替纯积分[1-7]，用于消除积分初值的影响，且能够抑制漂移。但在电机低速运行频率接近或者小于滤波器截止频率时，低通滤波器法会带来较大的幅值和相位误差。对此，文献[1]提出了3种算法将积分环节用低通滤波器和一阶惯性环节合成，前两种方案需要知道磁链幅值大小作为饱和函数的参数，磁链幅值的选取决定了算法的准确性，因此作者提出了基于正交模型的算法，此算法引入了闭环控制器，会在负载或者转速突变的动态过程中引入误差，所以该方法仅能对转子位置进行检测，不适用于闭环控制[2]。文献[3]用可调截止频率的低通滤波器替代积分器，该方法提高了电机低频运行时低通滤波器的性能，但是仍然存在相位和幅值的偏差[4]。文献[5]在低通滤波器后增加了幅值和相位的补偿环节，提高了全速度范围下低通滤波器的准确性。文献[6]在此基础上提出改进，调换低通滤波器与补偿环节的顺序，提高算法在转速突变时的动态性能。低通滤波器法只能够抑制零漂，不能够将其完全消除，为此文献[7-8]提出用带通滤波器替代纯积分环节，并对滤波器相位和幅值进行补偿，该方法的参数选取较为困难，算法的精度依赖参数选择。

本文在文献[6]的基础上进行改进，提出一种能够完全消除零漂的改进型磁链计算方法，用于永磁同步电机转子位置估算，并通过仿真和实验验证了该算法的有效性和可行性。

1 反电动势积分法问题分析

1.1 反电动势积分法原理

永磁同步电机α-β坐标系下的电压方程可表示：

(1)

式中：ψsα，ψsβ为磁链在α-β轴分量；usα，usβ为定子电压在α-β轴分量；isα，isβ为定子电流在α-β轴分量；Rs为定子电阻。

磁链方程在α-β坐标系表示如下：

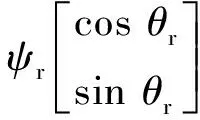
(2)

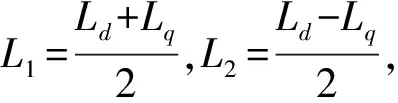
(3)

通过电压方程可得电压积分型定子磁链表达式：

(4)

通过以上公式可以求得转子位置，表达式如下：

(5)

在实际系统中电压电流并非理想正弦信号，纯积分环节受到电压电流漂移和积分初值的影响，导致位置估算不准确，从而无法进行无位置传感器的控制。

1.2 积分初值的影响

以α轴为例，将式(1)转换成离散表达方式：

ψsα(k)=ψsα(k-1)+[usα(k)-isα(k)Rs]Ts=

(6)

式中：ψsα(0)是初始时刻磁链，数值不随时间发生改变；Ts是采样时间。从式(6)可以看出，积分受到磁链初值的影响，产生偏置。

1.3 电流和电压的影响

反电动势积分法中参与计算的电压并非实际测量值，而是电压给定值。由于逆变器非线性的影响，实际电压不等于给定值，电流采样时由于采样电路的不对称性，及软件零位设置不准确，会产生偏置。把电流和电压的偏差用Δusα和Δisα表示，程序计算中电压电流可表示：

(7)

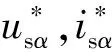
ψsα(k)=ψsα(k-1)+[usα(k)-isα(k)Rs]Ts=

(8)

可以看出，式(8)中存在一个偏差的累计量，如果直接采用纯积分的方案，积分结果将会发生漂移甚至饱和，从而影响磁链计算，导致无法获得正确的转子位置信息。

2 算法理论分析

为了解决纯积分带来的影响，本文在传统低通滤波器算法的基础上，提出了一种能够消除积分初值和零漂的改进算法。

2.1 传统低通滤波器算法

为了方便公式推导，电压电流磁链均以矢量的形式表示。将式(4)转换到幅频域上，可表示：

(9)

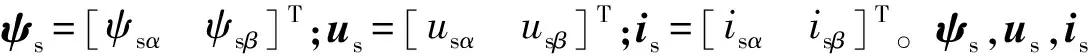
用一阶低通滤波器代替积分环节可表示：

(10)

由以上两式可以推导出：

(11)

从式(11)可以看出,当角速度ωe远大于截止频率ωc时，低通滤波器具有和纯积分相同的特性;但在电机低速运行时无法满足该条件，导致计算磁链相位超前幅值增大，降低截止频率会增大低通滤波器时间常数，导致动态性能下降。

2.2 幅值及相位补偿

由上可知，低通滤波器在输入信号频率较低的情况下将会带来较大的幅值和相位的偏差，为了提高滤波器在电机低速运行时的性能，需对低通滤波器的幅值和相位进行补偿。

由式(9)和式(10)可得：

(12)

可以得到其幅值和相位的关系：

(13)

交换低通滤波器与补偿算法的位置能够提高算法的动态性能[4]。以逆时针旋转方向为正，可以得到在α，β轴的补偿式：

(14)

(15)

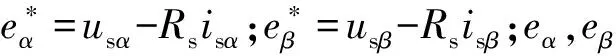
当含有直流量的信号通过低通滤波器时，直流量的衰减仅与截止频率ωc有关，截止频率ωc越大，抑制偏置的能力越强，但低通滤波器不能完全消除直流偏置，仅能够对其起到抑制的作用，所以为了消除直流偏置还需要进一步处理。

2.3 直流偏置的消除

文献[9]提出一种消除磁链积分零漂的方法。在α-β坐标系下，求一个正弦周期内磁链最大值和最小值的平均，即能得到当前时刻的磁链零漂值，下面以α轴为例说明零漂修正的原理。ψmax_α是磁链在α轴的极大值，ψmin_α是磁链在α轴的极小值，由此可以计算出磁链中的直流漂移量ψerr_α：

(16)

ψα=ψsα-ψerr_α

(17)

此算法通过求周期极值对漂移进行修正，算法每周期更新一次修正值，忽略了在周期内积分发生的漂移。假设：

usα-isαRs=Asin(ωet+B)+C

(18)

式中：A，B，C分别代表电动势的幅值相位以及偏置，将式(18)代入式(4)可得：

(19)

(20)

(21)

从式(21)可以看出，磁链分量中仍存在非正弦量，图7是零漂修正后的波形与发生漂移的纯积分波形对比。

图1 纯积分与零漂修正对比

可以看出，由于零漂修正值单个周期刷新一次，该算法不能够对磁链漂移进行实时的修正，在单个周期内计算结果仍然存在误差，并且在极值时刻出现突变。

本文将这种零漂修正算法与带补偿的低通滤波器(带补偿LPE)进行结合，提出一种能够完全消除直流偏置的算法，其结构如图2所示。

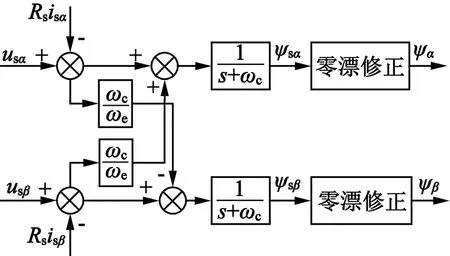
图2 改进算法结构框图

由上面分析可知，当直流量通过低通滤波器后，其输出仅与滤波器截止频率有关，不随时间发生变化，在通过零漂修正后能够消除该直流分量。图3是3种算法的对比结果，在输入信号中加入了5%的直流偏置。

图3 零漂修正、带补偿LPF和改进LPF

从图3上可以看出，带补偿LPE输出发生了偏置，而积分零漂修正算法在极值处出现了突变的情况，并且仍存在一定的误差，本文算法很好地消除了直流偏置。

3 仿真实验

为了验证改进低通滤波器算法的动静态性能，通过MATLAB/Simulink，搭建了永磁同步电机矢量控制仿真模型，电机参数如表1所示。

表1 电机参数

本文采用了id=0的矢量控制策略，由于电机在零低速时反电动势很小，无法用于转子位置估算，所以采用了速度开环起动的控制方式[10]，如图4所示。电机在起动时选择开关在1的位置，当电机到达10%额定转速时切换至开关2，工作于无位置传感器的闭环控制。

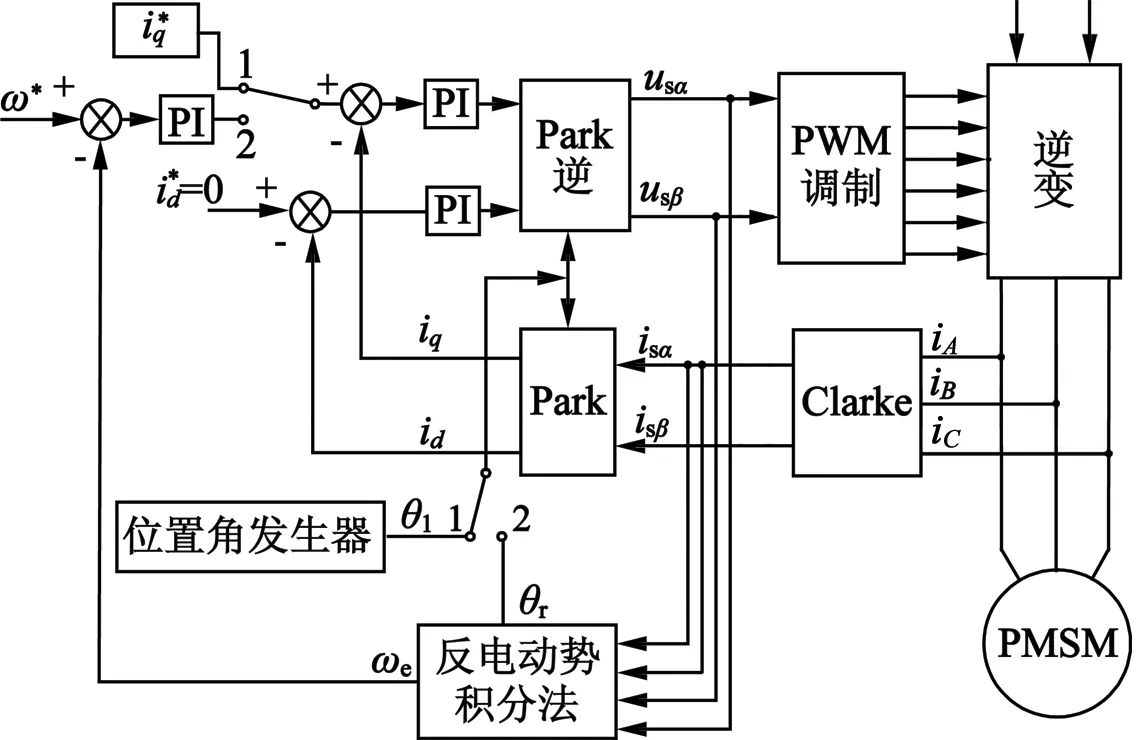
图4 无位置传感器矢量控制框图

3.1 算法稳态性能验证

首先验证了改进算法在稳态下的性能，并与纯积分算法进行对比。本文选取低通滤波器截止频率为10 rad/s，电机运行在平稳状态，转速400 r/min。下文以β轴仿真结果进行说明，图5是改进LPF法和纯积分的对比图，从图5可以看出，纯积分算法由于受到积分初值的影响发生了偏置，本文提出的改进算法能够很好地消除积分初值的影响，磁链计算结果几乎与参考曲线重合。

图5 纯积分、改进LPF的β轴定子磁链

为了验证算法对直流漂移的抑制能力，在β轴电流增加了0.5 A的直流分量。可以看出，在纯积分的算法下积分随着时间增加，误差累计发生漂移，本文提出的改进算法能够很好地消除直流分量带来的漂移，计算结果几乎和参考磁链重合。

图6 纯积分、改进LPF的β轴定子磁链

3.2 算法动态性能验证

为了验证算法的动态性能，电机给定转速在1 s时从200 r/min上升至500 r/min，并在β轴电流增加了1 A的直流分量，图7用带幅值和相位补偿的低通滤波器与改进算法比较，其中图7(a)是磁链观测结果，图7(b)是估算转子位置对比，图7(c)是估算转子位置误差对比。

(a) β轴定子磁链

(b) 转子位置

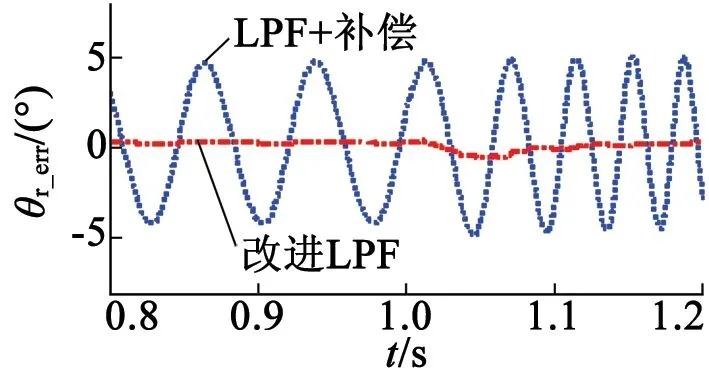
(c) 转子位置误差

从图7对比可以看出，本文提出的改进算法能够很好地消除直流偏置，补偿了低通滤波器的缺陷，并且动态性能优良。

4 实物验证

将本文改进的算法应用于实际永磁同步电机控制系统。将估算的转子位置和速度与编码器测量值进行比较，实验数据通过控制板上的DA进行输出，通过示波器进行观察。

图8是电机稳定运行在170 r/min，估算转子位置和速度与编码器测量对比。

(a) 估算转速与测量转速

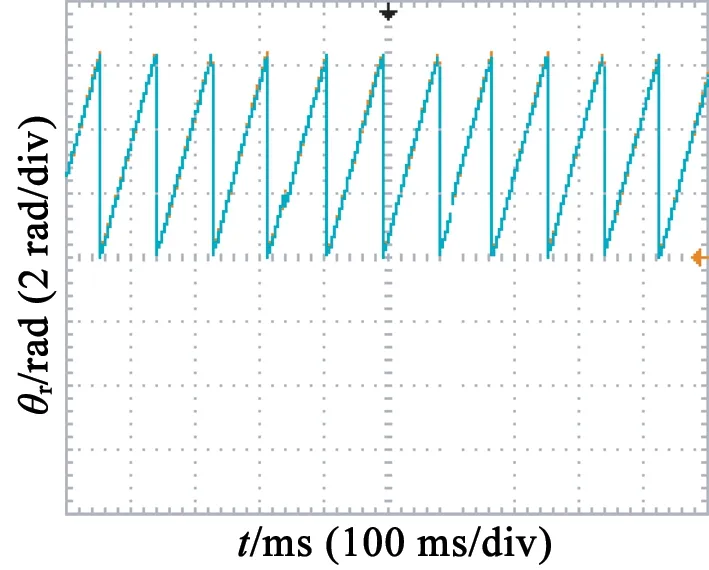
(b) 估算角度与测量角度

图9是电机转速由170r/min增加到245r/min，估算的转子位置和速度与编码器测量对比。

从实验测试可以看出，改进的LPF算法能够准

确估算转子位置与速度，估算结果与编码器测量比较，角度误差小于1.5%，无位置传感器运行时动静态性能良好。

(a) 估算转速与测量转速

(b) 估算转速与测量转速

5 结 语

本文在低通滤波器代替积分器的基础上进行了改进，结合了一阶低通滤波器结构简单的优势，解决了低通滤波器不能消除直流漂移的缺陷，最终通过实验验证了本文算法能够很好地消除积分初值和直流偏置的影响，算法计算量小，能够用于反电动势积分法无位置传感器控制。

[1]HUJ,WUB.Newintegrationalgorithmsforestimatingmotorfluxoverawidespeedrange[J].IEEETransactionsonPowerElectronics,1998,13(5):969-977.

[2]HOLTZJ,QUANJ.Driftandparametercompensatedfluxestimatorforpersistentzerostatorfrequencyoperationofsensorlesscontrolledinductionmotors[J].IEEETransactionsonIndustryApplications,2003,39(4):1052-1060.

[3] 张旭,瞿文龙.一种低速下磁链观测补偿的新方法[J].电工电能新技术,2003,22(3):50-54.

[4] 张星,瞿文龙,陆海峰.一种能消除直流偏置和稳态误差的电压型磁链观测器[J].电工电能新技术,2006，25(1):39-43

[5]LIYong,uangWenxin,uYuwen.owcostimplementationofstatorfluxorientedinductionmotordrive[C]//ProceedingsoftheEighthInternationalConferenceonElectricalMachinesandSystems.Piscataway,NJ,USA:IEEE,2005:1534-1538.

[6] 何志明,廖勇,何大为.定子磁链观测器低通滤波器的改进[J].中国电机工程学报,2008,28(18):61-65.

[7] 李彪,李黎川.新型磁链观测算法及其在永磁同步电机无位置传感器控制中的应用[J].西安交通大学学报,2015,49(11):102-109.

[8] 李红,罗裕,韩邦成,等.带通滤波器法电压积分型定子磁链观测器[J].电机与控制学报,2013,17(9):8-16.

[9] 王子辉.永磁同步电机全速度范围无位置传感器控制策略研究[D].杭州：浙江大学,2012.

[10]WANGZihui,LUKaiyuan.FredeBlaabjeg.Asimplestartupstrategybasedoncurrentregulationforback-EMFbasedsensorlesscontrolofPMSM[J].IEEETransactionsonPowerElectronics,2012,27(8):3817- 3824.