PMSM伺服系统中复合控制器设计及实现
杨 毅
(国网湖北省电力公司技术培训中心,武汉 430079)
0 引 言
随着永磁同步电机(以下简称PMSM)在不同运动控制领域的广泛应用,人们对PMSM控制系统的设计及性能要求也越来越高,不仅要求尽可能地降低生产成本,同时又要求系统可靠性高、控制精度高等。但实际应用中,由于电机本身固有的转矩脉动以及外界不确定干扰的存在,速度波动不可避免。速度波动的存在必然会影响控制系统的调速精度及定位跟踪精度,同时还会带来系统噪声及振动。
1 迭代学习补偿控制器设计
迭代学习控制实际上是一种误差修正算法,它通过学习之前储存的控制器误差信息以及输出信息,修正补偿控制器后续的输出信息,达到减小输出转矩脉动的目的。由于迭代学习方法非常适合具有周期性的运动控制,对于PMSM的周期性转矩脉动,迭代学习控制可以很好地补偿抑制。
1.1 迭代学习数学描述及学习律
迭代学习控制的基本做法是:对于一个做重复运动或周期性运动的轨迹跟踪控制,通过学习前一次或者前几次系统的输出误差信息和系统控制输入,不断地对控制器的输出进行优化,使得系统控制输入比上一次更接近于理想输入,从而达到优化控制的目的,如此不断重复,直至系统输出轨迹跟踪上期望轨迹[1]。
1.2 周期性转矩脉动的迭代学习补偿控制器设计
目前,对于PMSM周期性转矩脉动的抑制,电流型学习补偿控制是一种较常用的方法。但是,使用此法需要较准确的转矩信号,即需要对转矩信号进行实时的测量或者估计,可通过对速度波动进行学习补偿,从而间接地补偿系统周期性转矩脉动,达到减小PMSM伺服系统速度波动的目的。本文将选择基于P型的迭代学习律对转矩进行学习补偿。前人对迭代学习的初值问题进行了考虑[2],提出了带遗忘因子的迭代学习控制,遗忘因子的引入可以减弱初始扰动对系统的影响,同时在一定程度上可保证迭代学习的收敛速度[3-4]。综上所述,采用带有遗忘因子的P型开闭环迭代学习律。相应地,控制律:
uk+1(t)=(1-α)uk(t)+Φek(t)+Γek+1(t)
(1)
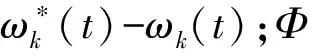
2 反步自适应滑模控制器设计
2.1 反步设计基本思想
反步设计是Krstic M, Kanellakopoulos I, Kokotovic P.V等学者提出的基于Lyapunov理论的递归设计方法,它是一种后推设计方法。相比于传统的Lyapunov设计方法,反步设计能够系统地构建Lyapunov函数以及反馈控制律[5]。使用反步设计方法对PMSM伺服控制系统进行设计已有很多的研究,其中,在电机控制器进行设计中I.Kanellakopoulos等人成功地设计并应用了反步设计方法[6]。
考虑如下单输入单输出系统
(2)
对于第一个子系统,期望的控制是对于给定xd,设计一种鲁棒的控制算法,实现x1对xd的准确跟踪。同时,将x2看作虚拟控制,需要设计相应的虚拟控制率,选取合适的Lyapunov函数,证明子系统的镇定性。同样的方法,可以对下一个子系统逐推设计,对上一个子系统得到的虚拟控制律进行准确跟踪,最后逐推直至完成整个系统的设计。以上即为系统反步设计的基本思想。
2.2 反步自适应滑模控制器设计
由于很多低速高性能伺服系统往往运行于低速甚至超低速状态,那么此时的伺服系统便不再是简单的调速系统。在一些应用场合,如控制力矩陀螺的控制中,不仅要求系统具有较好的速度平稳性,同时还要能够进行精确的位置跟踪操作,此时普通的调速系统难以同时胜任这种工作[7]。为此,设计的PMSM伺服系统在速度模式和定位模式两种工作模式下都是通过位置环实现的。这样既保证了低速时系统速度平滑性,同时增强了系统带载运行能力[8]。对于动态系统,考虑到系数不确定性和外部干扰的影响有:
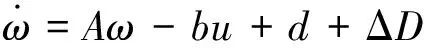
(3)
令d1=d+ΔD,则:
(4)
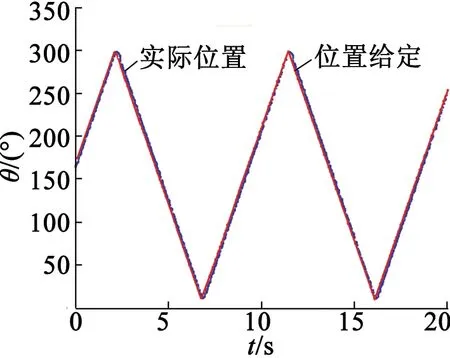
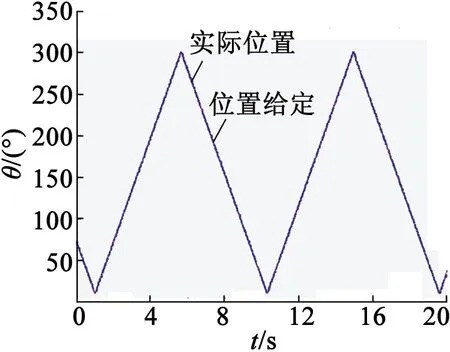
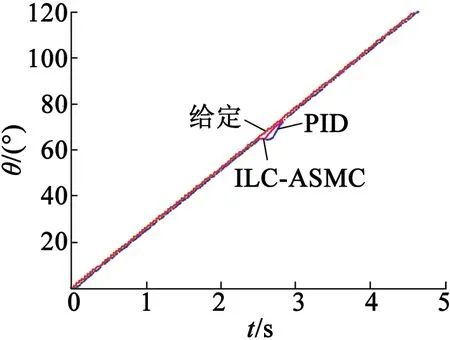
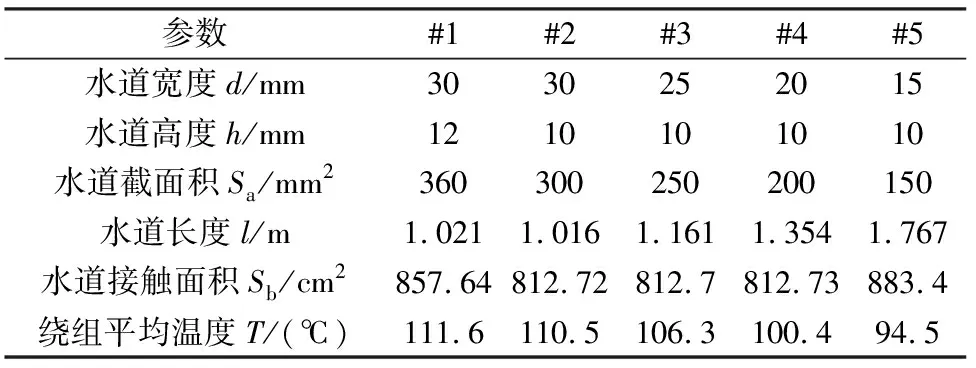
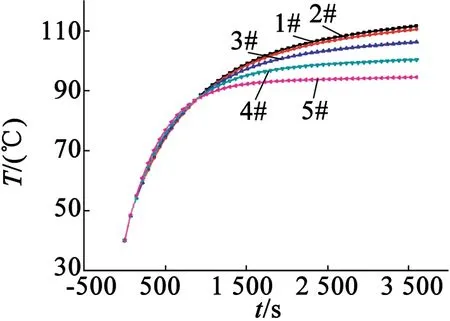
设系统干扰及不确定项d1有界,即有|d1| 鲁棒控制算法的设计和实现是控制总目标,在不确定项d1的影响下,实现转子实际位置θ对转子位置给定值θd的准确跟踪。 基于上述分析,系统针对位置子系统,将虚拟控制看作ω,考虑以下公式描述的Lyapunov函数: (5) 式中:字母θd表示转子位置;字母θ表示转子的实际位置。 对式(5)求导有: (6) 将虚拟控制项ω设计成: (7) 式中:k1>0。经过推导和整理,Lyapunov函数的导数可以表示: (8) 综上所述,在全局范围内虚设计的拟控制项ω*能够渐近稳定位置子系统。 进一步需要设计速度子系统,实现速度子系统对位置子系统得到的虚拟控制项的精确跟踪。 首先,速度跟踪误差项可以定义为ωe=ω-ω*,采用转子实际位置θ和ωe描述系统方程,具体可以表示: (9) 对于上述级联系统,考虑下述Lyapunov函数: (10) 式中:S=ωe为滑模函数,其导数: (11) 对上述Lyapunov 函数求导有: (θ-θd)[ωe-k1(θ-θd)]+ -k1(θ-θd)2(θ-θd)ωe+ (12) 设计速度环滑模控制律如下: (13) 将式(13)带入式(12)可得: -k1(θ-θd)2-η|S|+|Sd1|≤ -k1(θ-θd)2-η|S|+|S||d1| (14) 为了保证系统的稳定性,选择η>|d1|,此时: (15) 根据Barbalat引理,可得: (16) 即闭环系统是全局渐进稳定的。 至此,便完成了PMSM反步滑模控制器的基本设计。但上述设计存在着一个问题,由于滑模控制(Sliding Mode Control,SMC)的非连续控制部分是决定SMC强鲁棒性的主要因素,系统结构可以由SMC通过高频切换控制刻意地改变,从而将系统状态限制在滑模面上[8]。只有在预先确定外部扰动及系统参数不确定性的上界时,才能明确切换增益值的数值,即选择切换增益值η时,需要依赖于d1的上界dmax。但在多数情况下,dmax是未知的、不可获得的。一般情况,在切换增益选择时,为了保证系统的稳定性都会选择足够大的切换增益,需要注意的是,为了避免严重的抖动现象需要避免过大的切换增益[9]。因此,需要引入自适应机制,即实现切换增益的选择可以根据扰动量的大小实时自动更新。 (17) 式中:κ>0。同理,自适应滑模控制算法将由式(18)表示: (18) 定理:对于式(9)所描述的PMSM控制系统,如果采用式(17)的自适应律和式(18)的控制律,则闭环系统是渐进稳定的。 证明:选择Lyapunov函数: (19) 对上述Lyapunov函数沿系统轨迹求导,并将式(17)和式(18)代入式(19),可得: |S||d1|-|S|dmax (20) 由于dmax>|d1|,则有: (21) 根据Barbalat引理,可知: (22) 即PMSM伺服系统是全局渐进稳定的。 带遗忘因子的P型开闭环迭代学习控制在削弱周期性转矩脉动方面都能够起到很好的效果。迭代学习控制算法主要解决的是PMSM周期性转矩脉动问题,它对由于周期性转矩脉动引起的速度波动可以得到有效的抑制。然而迭代学习无法抑制非周期性转矩引起的速度波动及其他不确定性干扰[10]。因此,将迭代学习控制器得到的转矩脉动补偿量作为自适应滑模控制的输出补偿,构建一种复合控制,即基于迭代学习补偿的反步自适应滑模控制(简称ILC-ASMC),就可以使伺服系统在保证控制精度的同时,增强系统的鲁棒性及响应的快速性。基于反步思想设计的自适应滑模的控制律: (23) 由迭代学习控制得到的系统周期性转矩脉动补偿: uk+1(t)=(1-α)uk(t)+Φek(t)+Γek+1(t) (24) 将迭代学习得到的控制输出用于补偿自适应滑模控制器输出,便得到复合控制输出: (25) 在此复合控制系统中,系统的速度波动由迭代学习转矩脉动补偿器及自适应滑模控制器共同抑制。自适应滑模控制器对维持整个系统的稳定性、鲁棒性起主要作用,对由于系统参数变化等因素引起的速度波动可以得到很好的抑制。 搭建实验平台及驱动控制系统,用于对设计的迭代学习补偿的反步自适应滑模控制(ILC-ASMC)复合控制系统抑制速度波动能力、鲁棒性及响应的快速性进行验证。本实验平台包含一套PMSM驱动控制系统、PMSM、磁粉制动器和扭矩传感器。PMSM电机参数如表1所示。 表1 PMSM电机参数 对于设计的复合控制系统有效性验证主要从以下两方面进行:验证复合控制系统对速度波动的抑制能力和系统带载位置跟踪性能;同时,对复合控制系统的鲁棒性、抗干扰能力进行验证。 (1) 带载位置跟踪性能 为了验证设计的复合控制系统位置跟踪性能,图1给出了未使用迭代学习补偿与使用迭代学习补偿时,系统带载三角波位置跟踪曲线,负载大小3 N·m。同时基于三角波位置跟踪及误差数据可知,在使用迭代学习转矩脉动补偿前,三角波位置跟踪误差最大约5°;而在加入迭代学习补偿后,位置带载跟踪的精度明显提高,位置跟踪误差基本在2°以内。相比补偿前,补偿后位置跟踪误差减小约60%。因此,设计的复合控制在提高PMSM伺服系统位置跟踪精度上有很好的效果。 (a) 未使用迭代学习补偿 (b) 使用迭代学习补偿后 (2)鲁棒性验证 迭代学习控制对于抑制周期性转矩脉动具有良好的效果,但是对于未知的干扰及非周期性转矩却没有多大抑制效果,尤其在有突加的未知干扰情况下,其鲁棒性较差。然而自适应滑模控制在增强系统鲁棒性及响应的快速性上有着明显的优势。图2是位置给定为斜坡信号时,使用ILC-ASMC复合控制和PID控制时系统响应曲线;在t=2.5 s时突加了3 N·m的负载扰动。图2为自适应切换增益响应曲线。 从图2得到的斜坡跟踪曲线可知,复合控制对扰动响应的快速性明显优于PID控制,具有较强的鲁棒性。在t=2.5 s突加负载扰动时,复合控制能够更快地响应,并且及时地跟踪上给定信号;而PID控制时,系统的鲁棒性及快速性要差很多,控制效果不及本文设计的复合控制器。图3是系统自适应切换增益的响应曲线。在系统没有收到未知扰动的情况下,自适应机制可以迅速地根据扰动量的大小自动调节切换增益值,从而免去了对未知扰动上界的要求。 图2 斜坡信号位置跟踪 图3 自适应切换增益曲线 PMSM在低速运行情况下存在着诸多问题,其中低速转矩脉动及速度波动是影响系统性能的主要原因。迭代学习控制算法用于解决PMSM伺服系统周期转矩脉动的问题,设计了带遗忘因子的P型开闭环迭代学习控制器;然后在增强系统鲁棒性上,基于反步设计思想完成了自适应滑模控制器的设计;最后,将迭代学习获得的转矩脉动补偿量补偿到自适应滑模控制器输出中,构建了复合控制,在保证系统控制精度的同时增强了系统的鲁棒性。 [1] WANG Y Q ,GAO F R,Francis J.Doyle III.Survey on iterative learning control, repetitive control, and run-to-run control.Journal of Process Control,19(10),2012:1589-1600. [2] 林潜,葛宝明,毕大强,等.永磁同步电机控制硬件在环测试平台的实现[J].电工电能新技术,2014,33(3):76-80. [3] 张兴,郭磊磊,杨淑英,等.永磁同步发电机无速度传感器控制[J].中国电机工程学报,2014,34(21):3440-3447. [4] 佘致廷,董旺华,秦亚胜,等.基于反步滑模变结构的PMSM速度控制[J].控制工程,2016(S1):1-5. [5] 范越,马大为,吴跃飞.自适应反步滑模控制在火箭炮伺服系统中应用[J].火力与指挥控制,2014(6):86-89. [6] 刘芳璇,李益民,崔晶,等.基于ACA-BFA算法的PMSM自适应模糊滑模控制[J].电气传动,2015,45(11):58-61. 温度之差达到17 ℃,温度曲线如图12所示。 表2 不同水道仿真结果 图12 不同水道方案的绕组平均温度曲线 从以上分析可知,冷却水流量和入水口温度一定时,水的流速影响电机散热能力,同时水道接触面积也影响电机散热能力,在电机冷却系统设计时,需要结合电机的工艺要求和机壳强度,综合设计电机的水道,能有效降低电机温升。 经过仿真分析,#5的水道结构冷却效果最好,所以采用#5水道结构进行样机试制,实物样机和台架试验如图13所示,进行电机持续工况下稳态温升性能测试,电机绕组稳态温度为98 ℃,温升曲线如图14所示。 图13 样机实验台架 图14 样机实验值和仿真值对比 参数仿真值测试值绕组平均温度T/(℃)94.598 图14中,电机绕组稳态温度仿真值与测试值对比如表3所示,测试值与仿真值偏差3.7%,满足工程需求。 本文对新能源客车用驱动电机的温度场进行建模,仿真分析了电机持续运行工况的稳态温度场和短时运行工况的瞬态温度场,可知,此驱动电机的温升满足设计要求,可以可靠运行。同时,对该电机冷却系统进行了研究和优化,仿真和实验结果表明,圆周螺旋水道结构的散热效果最好,适合作为电动客车用高转矩密度电机的冷却水路,并且通过对电机水道的优化,可有效降低电机温升。 [1] 陈清泉,孙立清.电动汽车的现状和发展趋势[J].科技导报,2005,23(4):24-28. [2] 彭海涛,何志伟,余海阔.电动汽车用永磁同步电机的发展分析[J].微电机,2010,43(6):78-81. [3] 王晓远,高鹏,赵玉双.电动汽车用高功率密度电机关键技术[J].电工技术学报,2015,30(6):53-59. [4] 张鑫鑫.增程式电动汽车驱动电机及其温度特性研究[D].哈尔滨:哈尔滨工业大学,2013. [5] 曹君慈,李伟力,程树康,等.复合笼条转子感应电动机温度场计算及相关性分析[J].中国电机工程学报,2008,28(30):96-103.

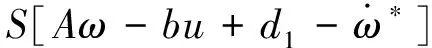

3 基于迭代学习补偿的反步自适应滑模复合控制器设计

3.1 实验平台及电机参数

3.2 ILC-ASMC复合控制系统验证

4 结 语
3.5 试验对比分析



4 结 语

