基于Python程序设计的PMSM气隙磁密分析

杜晓彬，黄开胜，蔡黎明

(1.广东工业大学，广州 510006;2.宁波供电局，宁波 315000)

0 引 言

随着永磁材料性能的提高，以及电机设计和控制技术的提升，永磁电机应用范围逐渐广泛。其中，永磁同步电动机(以下简称PMSM)具有体积小、结构简单、功率密度高的特点，被大量应用于生产实践中[1]。ANSYS有限元仿真采用有限元离散形式，将电磁场计算转化为矩阵求解，保证了计算的准确性和快捷性，通常采用ANSYS有限元仿真软件对电机进行仿真计算以及设计[2]。它提供的快速傅里叶分解工具可以对PMSM气隙磁密径向分布进行快速分析，为用户提供了方便。然而，进行快速傅里叶分解分析的结果可能会出现低次的谐波幅值比基波幅值大的情况，影响直观判断[3-4]，因此有必要开发设计软件对FFT分析数据进行后处理，以直观的图表形式展现傅里叶分析的结果。

Python语言是一种功能强大的开源编程语言，相对于C语言和Java，VB等其他编程语言，Python可以通过录入、调试更加少的代码来实现相同的功能，而且具有其他语言没有的强大的可移植性，可以实现在各个平台直接复制使用[5]。本文的程序开发直接基于Python，以实现更加广泛的使用。

本文以一台48槽8极表贴式磁钢的PMSM为例，应用Python语言进行程序设计，验证了程序的正确性，研究了极弧系数对电机气隙径向磁密谐波畸变率的影响。

1 PMSM的气隙磁场谐波分析

根据PMSM的原理，当电机通以对称的m相交流电流，定子在气隙中产生基波磁动势以及一系列不同次数、幅值以及转速的谐波磁动势[6-8]。转子磁钢则在气隙中产生基波磁动势和一系列的谐波磁动势。当定子上开槽，转子磁钢为表贴式时，气隙磁导除了平均磁导，还有一系列的磁导谐波分量，定转子磁动势以及气隙磁导相互作用产生了气隙磁场。

PMSM气隙中基波磁动势与平均气隙磁导相互作用，产生基波磁场bp=Bpcos(pθ1-ω1t)，p为电机极对数，ω1为电流的角频率，θ1为定子空间的圆周角坐标。可以看出，基波的极对数为p。

2 有限元仿真和Python程序设计

2.1 ANSYS-Maxwell 2D分析气隙磁场谐波

在PMSM中，电机的径向气隙磁场Br(θ,t)是沿着气隙圆周分布的，它是时间与位置的函数，可以在电机气隙中取一个固定时间点，并取沿着气隙一周的路径进行计算。

ANSYS-Maxwell 2D仿真软件计算中，气隙径向磁密表达式：

Br=BXcosθ+BYsinθ

(1)

式中:BX为磁密沿着x轴的分量;BY为磁密沿着y轴的分量。根据式(1)，沿着该圆周可以绘制出横坐标为空间位置，纵坐标为径向磁密的波形图。一般在工程技术上取该圆周半径为定子内径与转子外径的均值的一半，即：

(2)

由ANSYS-Maxwell 2D提供了对波形图进行快速傅里叶分解的工具FFT，可以将Br波形图分解为各次谐波以及对应的磁密谐波幅值大小，并表示为横坐标为空间位置d，纵坐标为谐波幅值的傅里叶分解图。其中，空间位置所对应的谐波极对数以及次数分别是：

(3)

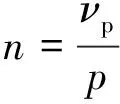
(4)

式中:vp为谐波极对数;n为谐波次数。当v为分数时，谐波为间谐波；当n为整数时，谐波为整数次谐波。

2.2 Python程序设计

为了简化对ANSYS-Maxwell 2D快速傅里叶分析的数据处理，以直观方便的形式从快速傅里叶分解的数据中筛选出用户想要的结果，开发了本程序。程序基于语言简洁的Python语言，以图表的形式直观地表示出各次谐波以及对应的谐波幅值，并快速计算出该波形的谐波畸变率，节省了对波形数据处理的时间。

2.2.1 Python程序设计内部流程

本程序设计的主要模块如图1所示。

图1 Python设计程序的模块示意图

Python程序分析流程主要有3个模块。第一模块是对电机参数包括电机极对数p、定子内径D1、转子外径D2的读取和对气隙径向磁密快速傅里叶分解数据Data.csv的读取。该模块是程序分析的前提。第二模块是将数据Data.csv中的D换算成谐波的次数 。通过用户给出的谐波次数以及幅值的筛选条件，在大量的谐波中筛选出次数比较小、幅值比较大的谐波。该模块是程序分析的主要部分。第三模块是对处理完成的结果进行输出，输出内容为隙磁密谐波畸变率THD值以及谐波幅值柱状图。其中，程序的各个模块具体流程叙述如下：。

(1)变量定义部分

程序包含了8个变量的定义，包括电机极对数p、定子内径D1、转子外径D2、圆周半径R、谐波极对数vp、谐波次数n、筛选谐波次数限定值nc、筛选谐波幅值限定值nm。其中，为了计算结果有较高的精度，将定子内外径、圆周半径、筛选谐波幅值限定值设定为float数据类型，而其他参数则设置为int数据类型。

(2)读取Data.csv数据文件部分

该部分主要对应第一模块第一步，对傅里叶分解的数据进行读取工作，是程序分析的前提。由于从ANSYS-Maxwell 2D导出的原始数据文件Data.csv是以列表格式展现的，即第一列为空间位置数据，第二列为谐波幅值数据，故需要对数据文件进行读取并对数据表格执行按列拆分功能。在程序中使用with open(file, 'r') as stream命令实现以上功能。

(3)读取电机参数部分

该部分主要对应第一模块第二步骤。主要读取输入的电机极对数p、定子内径D1、转子外径D2。

(4)计算部分

该部分对应第二模块的第一步骤。首先按照公式(2)计算该电机模型的气隙圆周半径R，其次按照式(3)与式(4)将读取的空间位置数据依次换算成气隙磁密谐波极对数和谐波次数。其中，对谐波极对数的次数取值为Fraction分数类型，以适用于分数槽集中绕组单相电机等其他机型运行过程中产生的间谐波。

(5)筛选谐波部分

该部分对应第二模块的第二步骤。由用户手动输入筛选谐波的限制条件，即筛选谐波次数限定值nc和筛选谐波幅值限定值nm两个条件，利用Python中filter函数，根据用户需求按照谐波幅值以及谐波次数条件进行筛选。

(6)绘制谐波图部分由以上第(4)部分的计算结果以及第(5)部分用户的筛选结果，调用Matplotlib绘图库进行绘制bar图，并以谐波次数为横坐标，各次谐波幅值为纵坐标。

(7)计算THD部分

该部分对应第三模块的第二步骤。在该部分定义函数THD(G)进行计算气隙磁密谐波畸变率，其中，参数G为由第(5)筛选的谐波次数所对应的谐波幅值数组，并调用sqrt函数与sum函数完成计算功能。

为了进一步清晰地说明本程序的算法流程，给出程序流程图如图2所示，并包含了以上说明的三部分模块的功能。

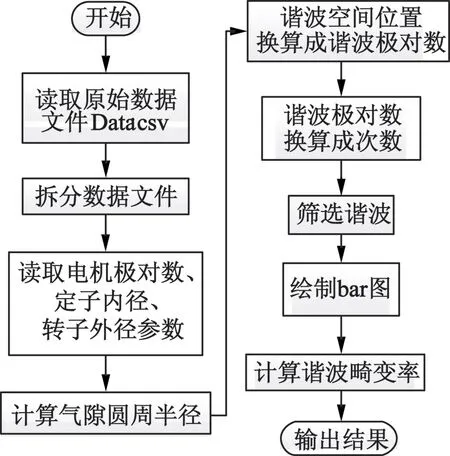
图2 设计程序流程图

2.2.2 ANSYS-Maxwell 2D与Python数据交互

本程序拥有友善的HCI界面，使用者可以在完全不考虑程序内部结构和内部特性的情况下，而直接使用它对数据进行分析处理，直接得出想要的结果。该程序与ANSYS-Maxwell 2D的交互过程如图3所示。

图3 数据交互传递过程

在ANSYS-Maxwell 2D仿真软件建立PMSM有限元模型，进行仿真分析计算。计算完成后通过Draw circle命令绘制半径为R的圆周，再通过Creat Transient Report命令绘制气隙径向磁场波形图。完成之后通过Perform FFT on Report对波形图傅里叶分解，得到关于空间位置和谐波幅值的傅里叶分解数据Data.csv。

打开Python分析程序Analyze.py，将Data.csv数据导入到分析程序中，输入筛选的限制条件：谐波次数条件以及谐波幅值条件。该程序可以进行单一条件筛选或者两个条件同时筛选，以满足用户的多种需求。对数据进行分析筛选完成以后，分析结果以横坐标为筛选谐波的次数，纵坐标为筛选谐波的幅值的Bar Plot图形呈现，并计算出该径向谐波的畸变率THD。

3 有限元仿真分析与程序应用

以一台8极48槽表贴式磁钢的PMSM为例，仿真分析其额定负载时电枢磁场的径向磁场以及额定负载时气隙磁场的径向磁场。

3.1 额定负载时电枢磁场径向磁场谐波分析

鉴于需要分析定子绕组产生的径向磁场磁密，故删去ANSYS-Maxwell 2D电机模型中转子上的磁钢，然后进行仿真计算，单独分析定子绕组在气隙中产生的磁场。建立电机模型如图4所示。

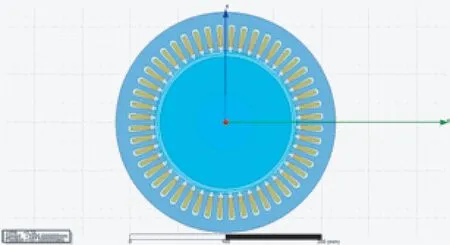
图4 PMSM电枢磁场仿真模型

仿真结果通过ANSYS-Maxwell 2D自带的FFT工具进行傅里叶分解，将分解结果数据保存为Data.csv文件。再通过Python程序分析，输入筛选的限制条件：谐波次数为25及以下，谐波幅值大于0.005 T。并由Python程序直接绘出谐波图如图5所示，并计算出气隙径向磁密谐波畸变率的大小。

图5 额定负载电枢磁场谐波

通过图5可以看出，对定子绕组额定负载情况进行仿真，基波幅值最大为0.614T，谐波包含有5，7，11，13，17，19、25等次数。由于11，13次为一阶齿谐波，谐波含量比较大。通过Python程序分析直接得出谐波此时畸变率为26.99%。符合上述关于PMSM的定子绕组磁场谐波的原理。

3.2 额定负载时气隙径向磁场谐波分析

在ANSYS-Maxwell 2D电机模型中，保留转子上的磁钢以及定子上的绕组，对气隙中磁密进行仿真计算仍由Python设计程序进行分析，结果如图6所示。

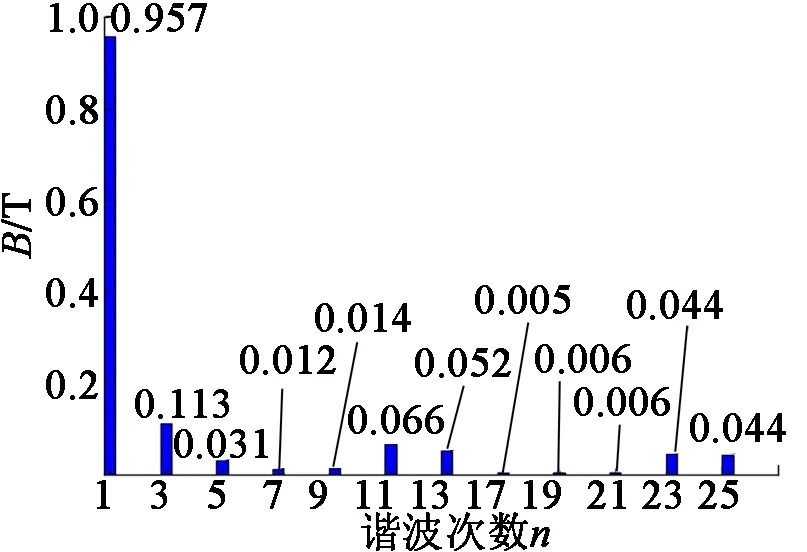
图6 额定负载气隙磁场谐波

由图6可知，气隙中的径向磁密主要以奇数次磁密为主，其中，基波的幅值最大为0.957 T，谐波幅值以3，11，13次谐波幅值为主。谐波畸变率为16.56%。

通过以上仿真计算以及基于Python程序的对于数据的处理，验证了程序的可靠性与实用性。

3.3 极弧系数对径向磁密THD的影响

利用Python程序能快速地计算出谐波畸变率的特点，通过ANSYS-Maxwell 2D的参数化分析工具以及Python程序来进行仿真，分析极弧系数对径向磁密THD的影响。仿真结果如图7所示。

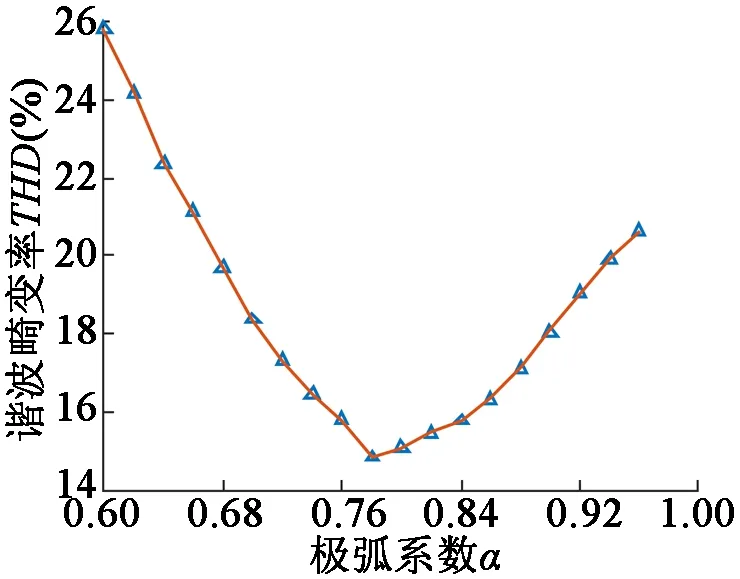
图7 极弧系数对气隙径向磁密THD的影响

由图7可知，当选择不同的极弧系数时，谐波畸变率有不同的数值，且曲线呈现先下降后上升的趋势，当选择极弧系数为0.78时，THD有最小值14.81%。

由于当径向气隙磁密波形中的谐波含量越小，谐波畸变率会越小，谐波幅值越小。所以，在谐波磁场次数一定时，通过改变磁钢的极弧系数来降低谐波幅值[9-11]。

由此可见，通过选择恰当的极弧系数可以抑制谐波畸变率，使谐波更加趋近于正弦。

4 结 语

本文设计了一个基于Python的程序，用于对ANSYS-Maxwell 2D进行径向磁密分析的数据进行后处理，它能准确快速地绘制出谐波图形和计算出气隙磁密THD值，节省了用户的时间。通过仿真一台48槽8极PMSM，验证了程序的实用性和准确性。鉴于该程序能快速计算THD，利用该程序分析了不同极弧系数对径向磁密谐波畸变率的影响。通过该方法，得出极弧系数对磁密谐波畸变率的影响规律。本文的程序设计思路以及方法为分析旋转电机的气隙径向磁密提供了参考。

[1] 蔡黎明.永磁同步电动机电磁振动与噪声的研究[D].广州：广东工业大学,2016.

[2] 赵博.Ansoft 12在工程电磁场中的应用[M].中国水利水电出版社,2010.

[3] 谭建成.永磁无刷直流电机技术[M].机械工业出版社,2011.

[4] 段世英.分数槽集中绕组永磁同步电机的若干问题研究[D].武汉：华中科技大学,2014.

[5] Python核心编程[M].机械工业出版社,2001.

[6] 黄国治,傅丰礼.中小旋转电机设计手册[M].中国电力出版社,2007.陈仲才.

[7] 王秀和.永磁电机[M].中国电力出版社,2011.

[8] 许实章.交流电机的绕组理论[M].北京.机械工业出版社,1985

[9] 肖庆优,黄开胜,陈文敏,等.一种确定永磁同步电动机最佳磁极偏移角度的方法[J].微特电机,2015,43(12):14-16.

[10] ZHENG P,ZHAO J,HAN J,et al.Optimization of the magnetic pole shape of a permanent-magnet synchronous motor[J].IEEE Transactions on Magnetics,2007,43(6):2531-2533.

[11] LI Y,XING J,WANG T,et al.Programmable design of magnet shape for permanent-magnet synchronous motors with sinusoidal back EMF waveforms[J].IEEE Transactions on Magnetics,2008,44(9):2163-2167.