基于扰动补偿的PMSM转速环自抗扰控制器设计

谢传林，曾岳南，王发良，曾祥彩

(广东工业大学，广州 510006)

0 引 言

自抗扰控制器(以下简称ADRC)作为应用于永磁同步电机(以下简称PMSM)控制中的一种非线性算法，能够对系统的内、外扰动进行估计并给予补偿，不依赖于对象模型[1]。扩张状态观测器(以下简称ESO)作为ADRC的核心部分，其观测精度越高，系统的控制性能越好。然而在系统实际运行中，ESO所估计的扰动量较多且变化幅度很大，使得ESO难以保证对扰动有较高的估计精度，导致扰动不能够完全补偿，影响了ADRC的控制性能。为此，国内外学者进行了大量的研究，文献[2]提出了基于负载观测的自抗扰控制器设计，但是扰动补偿范围较小。文献[3]提出了基于滑模控制的模型补偿自抗扰控制器设计，利用辨识算法估计出转动惯量和负载转矩，从而减轻了ESO的观测负担，但由于滑模控制开关的切换动作所造成的控制不连续性，抖振现象无法避免。

针对上述问题，本文设计了基于扰动补偿的ADRC。首先通过参数辨识的方法估计出转动惯量和负载转矩，把部分扰动项表示出来并补偿到ADRC的扰动观测输出中，减小ESO的观测负担，提高ESO对扰动量的观测精度，进而增加转速环抗扰性能。最后根据基于带宽的参数整定方法得到控制器参数，通过仿真和实验表明，转速环采用基于扰动补偿的ADRC与采用线性ADRC相比，抗扰性能更优越。

1 PMSM数学模型

对于表贴式PMSM在d-q旋转坐标系下的电压和磁链方程可以表示：

(1)

(2)

电磁转矩和运动方程：

(3)

(4)

式中：ud，uq分别为定子d，q轴电压；id，iq分别为定子d，q轴电流；L为定子电感；ψd，ψq分别为定子磁链d，q轴分量；ψf为转子磁链；ω为转子电角速度；ωr为转子机械角速度；Rs为定子电阻；p为电机的极对数；Te为电机的电磁转矩；TL为电机负载转矩；J为转动惯量；B为电机的摩擦系数。

2 转速环控制器的设计

2.1 基于扰动补偿的自抗扰控制器设计

线性自抗扰控制器(以下简称LADRC)具有参数整定方便、算法简单等优点，它包括线性跟踪微分器(以下简称LTD)、线性扩张状态观测器(以下简称LESO)以及线性状态误差反馈(以下简称LSEF)3个部分[4]。根据式(4)可知，转速输出为一阶微分方程，因此选取一阶LADRC作为转速环控制器[4]。通过转动惯量辨识和负载转矩观测得到部分扰动项，并将补偿到ADRC扰动估计输出项中，同时与LSEF对总扰动的补偿一起组成控制量，实现转速反馈对转速给定的跟随。

由式(3)、式(4)可得：

(5)

(6)

式中：b0为可变参数。可得：

(7)

式中：fω为总扰动量。令x1=ω，x2=fω，u=iq，式(6)可写为：

(8)

为了LESO设计方便，将式(8)写为：

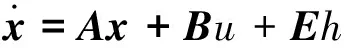
(9)

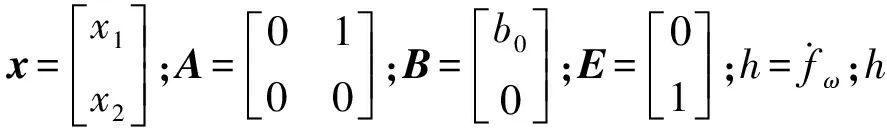
为了得到扰动量的数值，由式(9)设计的LESO的方程：

(10)

式中：β1,β2表示LESO的增益；z1,z2表示状态量的观测值；x1表示状态量的实际值。

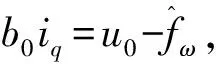
(11)

通过扰动补偿后，转速开环可由一个积分环节来表示。因此，选取比例控制作为控制律，即:

(12)

(13)

图1 转速环采用基于扰动补偿ADRC结构图

2.2 转动惯量的辨识

由于采样时间很小，可以得出：

(14)

式中：Ts为采样周期。

将式(14)代入到式(7)中，可得：

ωr(k)=ωr(k-1)+(Ts/J)·

[Te(k-1)-TL(k-1)]

(15)

由于机械负载转矩在两个采样时间内变化很小，可以看作恒定，因此对于式(15)中的负载转矩有：

TL(k)=TL(k-1)

(16)

由式(15)可得：

ωr(k-1)=ωr(k-2)+(Ts/J)·

[Te(k-2)-TL(k-2)]

(17)

联立式(15)、式(17)可得：

ωr(k)=2ωr(k-1)-ωr(k-2)+

b(k-1)U(k-1)

(18)

式中：U(k-1)=Te(k-1)-Te(k-2)；b(k-1)=Ts/J。

将式(18)作为转动惯量辨识的参考模型，即：

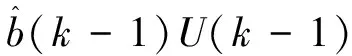
(19)

利用梯度校正估计算法[5-6]，可得：

(20)

由式(20)可以得到转动惯量的估计值：

(21)

2.3 负载转矩观测器的设计

由式(5)得：

(22)

由于负载转矩不易直接测量，可以通过已获得的iq，ω来观测。由于测量iq和ω时会有噪声误差的存在，使测量值不准确，因此为了得到精确的测量值，在负载转矩观测器的输出端加入一阶低通滤波器[7]，加入滤波器后式(22)变为：

(23)

式中：T1为一阶低通滤波器的时间常数。

将式(23)进行拉氏变换并整理可得：

(24)

对A取拉氏反变换可得：

(25)

联立式(24)及式(25)可得：

(26)

3 仿 真

在MATLAB/Simulink平台上搭建转速环，采用基于扰动补偿的ADRC双闭环调速系统仿真模型，电机参数如表1所示，并和转速环采用LADRC的控制效果进行对比，其参数整定是基于转速环带宽指标[8]，如表2所示。转速环参数可按表2给出的计算方法得到，其中：ωcv，ω0以及b0分别为200，1 000以及50。电流环均采用PI控制器，PI参数由工程整定方法可得[9]。

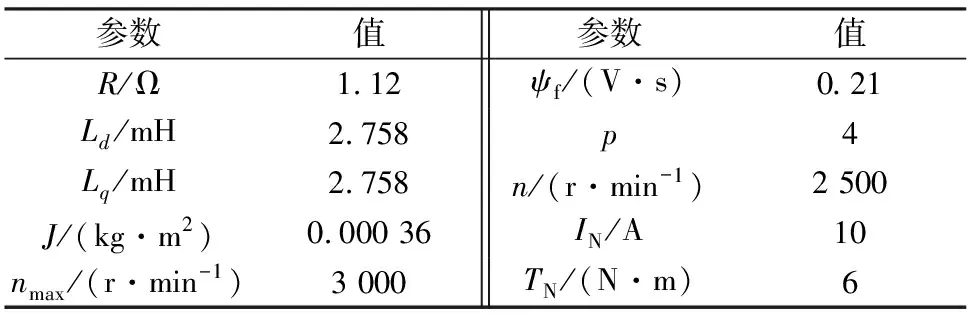
表1 伺服电机参数

表2 转速环一阶LADRC整定公式

表2中ωcv为转速闭环带宽；ω0为观测器带宽，取ω0=5ωcv～10ωcv；τ为LTD的惯性时间常数。

当转速给定1 000r/min，在0.5s时突加50%额定负载时，采用LADRC和基于扰动补偿的ADRC控制的系统转速响应如图2所示，观测器对扰动的跟踪波形如图3所示，系统总扰动量如图4所示。由图2、图3可知，采用基于扰动补偿的ADRC控制的系统在突加负载后，可以更快地恢复到稳态，转速跌落更小。而采用LADRC控制的系统在突加负载后，转速恢复时间更长，转速跌落也更大。

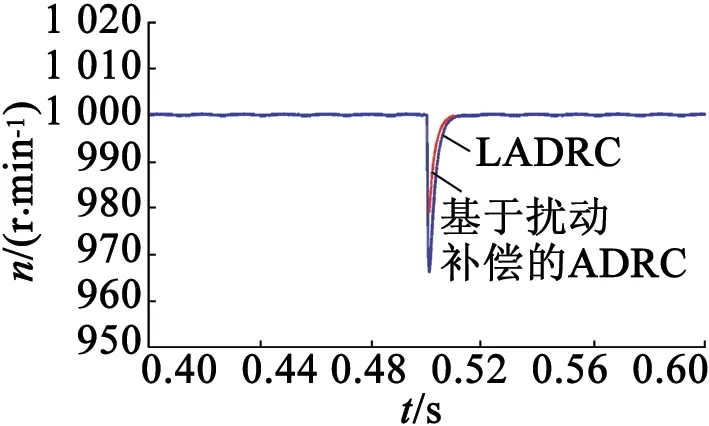
图2 突加负载时转速响应曲线

图3 扰动观测值对比

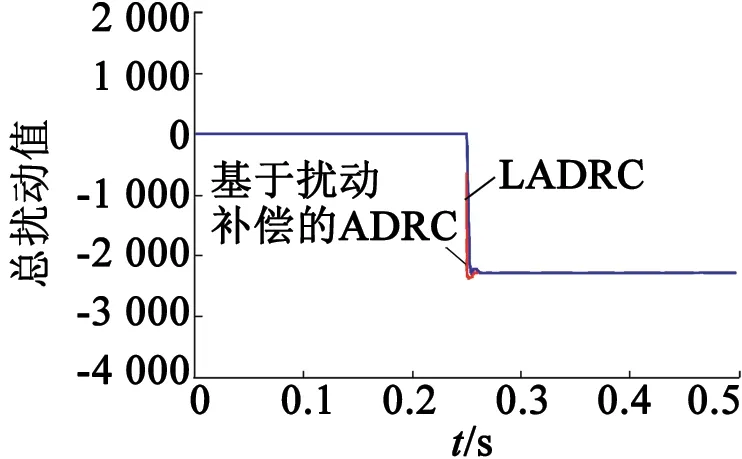
图4 总扰动对比

4 实 验

上述理论通过实验验证其有效性，实验中的参数设置条件与仿真参数相同。实验平台如图5所示。

图5 加载实验平台

抗负载扰动性能实验：转速给定为1 000r/min，转速达稳态后突加50%额定负载，采用LADRC和基于扰动补偿的ADRC控制的系统的转速跌落如图6所示，由图6可知，在负载转矩扰动作用下，采用基于扰动补偿的ADRC控制的系统抗负载扰动效果优于采用LADRC控制的系统。

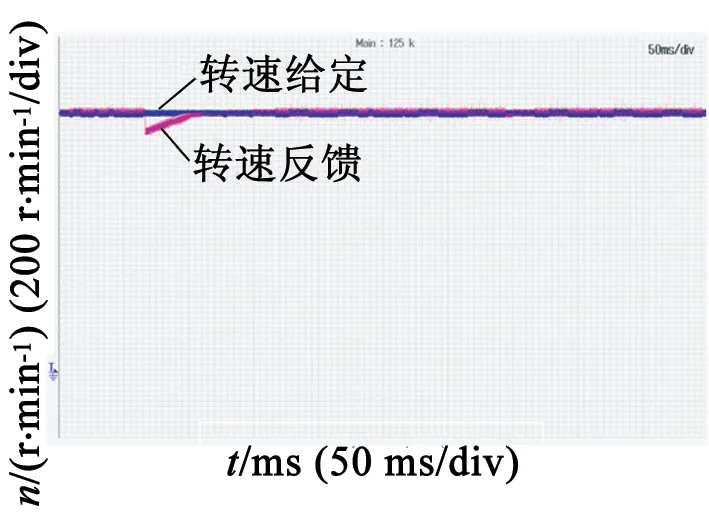
(a) 采用LADRC转速响应波形

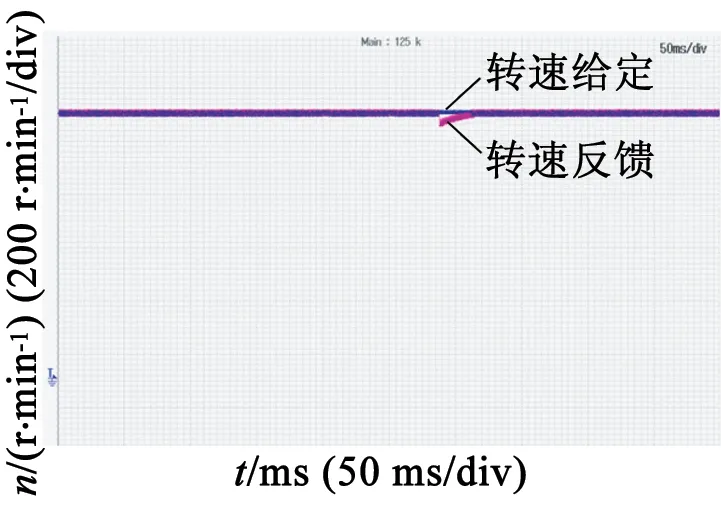
(b) 采用基于扰动补偿的ADRC

5 结 语

本文在线性自抗扰控制技术的基础上，辨识了负载转矩以及转动惯量，设计了基于扰动补偿的ADRC，并将其应用于PMSM转速环控制。仿真和实验表明，基于扰动补偿的ADRC有效减小了观测器的观测负担，提高了扰动估计精度，具有更好的抗负载扰动能力，有效抑制负载变化对转速的影响。

[1]HANJQ.FromPIDtoactivedisturbancerejectioncontrol[J].IEEETransactionsonIndustrialElectronics,2009,56(3)：900-906.

[2] 盖江涛，黄守道.基于负载观测的永磁电机驱动系统自抗扰控制[J].电工技术学报,2016,31(18):29-36.

[3]CHENHJ，XUH，LIUB，etal.ThecompensatedactivedisturbancerejectioncontrollerbasedonslidingmodecontrolforPMSM[C]//The5thAnnualIEEEInternationalConferenceonCyberTechnology，2015：240-245.

[4] 曾岳南，曾祥彩.永磁同步电机调速系统自抗扰控制器的设计[J].电气传动,2017(4):3-6.

[5] 沈艳霞，刘永钦.基于改进型模型参考自适应的PMSM参数辨识[J].电气传动,2009,39(5):47-50.

[6] 章玮，王伟颖.基于降阶负载扰动观测器的永磁同步电机控制[J].机电工程,2012,39(7):821-832.

[7] 刘志刚，李世华．基于永磁同步电机模型辨识与补偿的自抗扰控制器[J].中国电机工程学报，2008，28(24)：118-123．

[8]GAOZQ.Scalingandbandwidth-parameterizationbasedcontrollertuning[C]//ProceedingsoftheAmericanControlConference.Denver：IEEE，2003：4989-4996.

[9] 阮毅，陈伯时.电力拖动自动控制系统-运动控制系统[M].4版.北京：机械工业出版社，2012.