随机均衡配流下的连续性交通网络设计*
田晟 马美娜 许凯
(华南理工大学 土木与交通学院, 广东 广州 510640)
交通网络的设计和分析可以表述为一类带有用户均衡约束的网络优化问题,这类问题长期以来被认为是交通科学领域最难、最具有挑战性的问题之一.设计可靠和有效的交通网络,可以在最大限度利用道路资源的同时为出行者提供高效、快捷的服务.
近年来,国内外学者研究了各类网络设计问题的建模和算法.为了能够最大限度地为用户服务,学者们进行了基于出行者行程时间及其可靠性的研究.Sun[1]提出了一种基于随机需求的连续网络设计问题,并指出对于不同旅行时间的路段通行能力的拓宽需要采用不同的方法.Tong等[2]通过构建随时间变化的交通空间网络,制定了线性整数规划模型,使道路用户在行程时间预算内到达最多数量的活动地点.Yao等[3]提出了考虑路段行程时间可靠性的公交网络优化,最大限度地提高乘客出行效率.Avinash等[4]研究了用户收到不确定网络信息时的连续网络设计问题,并运用两种算法(量子遗传算法及一般的遗传算法)和代替评价函数考虑提供信息的用户行为.刘慧等[5]在交通网络设计中引进α- 鲁棒解,详细分析了期望行程时间与最大遗憾值之间的权衡关系.而关于网络道路资源的利用程度,国内外学者也从不用的角度提出了许多观点.Chen等[6]系统地阐述了不确定环境下的连续网络设计问题,并提出了基于容量和旅行时间可靠性的双目标网络设计模型.Wang等[7]根据需求的不确定性提出了新的双目标规划模型,该模型可以在满足加权平均数和标准差要求的基础上,最大限度地提高网络备用容量,而且可以用来评估各种排放和需求的影响对可持续发展的约束.孙飞等[8]通过建立考虑速度限制和环境污染的双层规划模型,解决了提高交通运行效率的问题.
以上研究在对交通流进行分配时均使用确定性均衡分配模型,而实际上,出行者在交通行为中会表现出不同的属性.除此之外,对道路本身一般只考虑路段的旅行费用,很少考虑其他的路网评价指标,从交通管理者的层面来讲考虑不够全面.可达性作为城市道路网评价指标之一,可以评价路网在空间构造和道路等级划分方面的合理性.基于此,文中在传统网络设计的基础上,考虑所设计网络中的节点可达性,建立了双层规划模型,通过改变部分路段的通行能力来影响交通流量的分配,从而使路网结构更加合理,以期更好地满足出行者的交通需求.该模型上层规划是从交通管理者的角度出发,通过考虑路网中的节点可达性来完成对路网中道路的扩建,下层规划则通过随机用户均衡交通分配模型来实现对路网中流量的分配.
1 交通网络设计中的双层规划模型
1.1 上层规划模型
可达性是反映交通成本的基本指标之一,它可以描述交通网络中各节点相互作用的机会.可达性反映节点在交通网络中的相互作用,因此网络中所有节点的可达性便可反映该网络的便利性.关于节点可达性的计算方法很多,文中结合交通网络设计的影响因素及交通网络的特性,建立了综合考虑路段阻抗函数、节点重要度等因素的节点可达性模型.
借助评价可达性常用的距离度量法[9],在一个OD(起讫点)对有多条路径的交通网络中,节点i的可达性如式(1)所示:
(1)

在实际的交通网络中,大多数出行者出行的首要考虑因素是时间最短,如果出行者均选择最短路径,结果可能导致该路径拥挤,从而增加出行时间.为了弥补距离度量法只考虑距离因素这一评价指标造成的对实际出行时间的忽视,在可达性的评价中引入路段阻抗函数[10]:
(2)
式中,ta(0)为路段a自由流走行时间,qa为路段a的交通流量,ea为路段a的原有通行能力,ya为路段a增加的通行能力,α、β为阻抗影响参数.
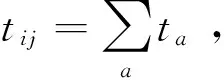
(3)
由于交通分区之间的流量吸引不同,即有不同的重要度,可达性的差异化是由不同的土地利用模式导致的.节点在网络中的位置和连接方式可以体现节点的重要性,如式(4)所示:
Ii=γni+(1-γ)cni
(4)
(5)
式中,Ii为节点i在路网中的重要度,ni为直接与节点i相连的路段数量,cni为节点i的凝聚系数,mi为与节点i直接相连的节点之间路段的总数,γ为指标所对应的权重.
当网络中节点的连通度很大时,节点本身的重要性便相对很小,在这种情况下,删除该节点基本不影响网络中交通流量的出行效率,即节点的凝聚系数cni大,因此凝聚系数是节点重要度的正向评价指标[11],指标对应的权重可以由熵值法确定.
综上,整个交通网络的可达性可认为是所有节点的可达性之和,将路网的可达性用所有节点的可达性的加权求和值表示,以节点可达性的重要度为权重,可将上层规划表示为
(6)
s.t.
(7)
式中,A为所有路段集合,Ga为扩建路段a的成本函数,B为投资金额.
式(7)的约束条件为拟扩建道路不超过预算投资和决策变量取值限制.
1.2 下层规划模型
传统的交通分配模型大多假设出行者是完全理性的,以出行的阻抗最小、效用或可靠性最大作为路径选择准则,较少考虑出行者的有限理性问题,导致交通分配结果存在一定偏差[12],这样的假设是不符合实际情况的.在实际的交通网络中,每一位出行者的理解出行时间是不同的,因此每条路段上的理解出行时间应该是一个随机变量.鉴于此,文中提出引入随机用户均衡配流模型.在该模型中,理解路段出行时间是实际路段出行时间与随机项之和,即
Ta=ta+εa
(8)
式中,Ta为路段a的出行者理解出行时间,εa为路段a出行时间的随机误差.
假设E[εa]=0或者E[Ta]=ta,即路段理解出行时间的平均值等于该路段实际出行时间,并假设εa是完全相同且独立分布地服从Gumbel分布的随机变量(独立同分布),则选择概率可被理解为Logit路径选择概率,根据这个Logit选择模型,路段流量由相应的路段成本决定.
在实际的交通网络中,当OD对间可以选择的路径之间的出行量满足Logit模型[13]时,即
(9)
(10)
通常情况下,城市道路交通网络的θ值会比地铁系统的小一些,因为地铁系统在出行时间上有相对较高的可靠性.不同θ取值下的OD出行需求不同,随着θ的增大,OD出行需求呈递减并逐渐收敛的趋势,当θ→∞时,随机均衡分配的结果近似于确定性用户均衡的分配结果,如果当θ取值a时OD出行需求趋于收敛,则θ的取值范围为(0,a).
综上,以Logit形式的流量随机加载为基础,构建Fisk随机均衡配流模型[14],具体的考虑路段能力约束的下层规划为
(11)
s.t.
(12)
式中:W为所有OD对集合;Rω为OD对之间的路径集合;gω为OD对之间的出行量;δar为路段与路径的关联关系,若路段a经过路径r,则δar=1,否则δar=0.
式(12)中约束条件表示:起讫点交通流量为所有路径流量守恒、路段流量为所有路径中经过该路段的流量之和、路段流量不超过扩建后的道路通行能力.
该模型没有考虑均衡路段排队延迟,这是因为只有在路段流量达到路段通行能力时延迟才会出现.Bell等[15]还证明,当且仅当所有达到通行能力的路段约束相互独立时,随机均衡分配的延迟才是唯一的.
可以看出,对高校决算报表分析的重要性认识比较一致,这也是当前中国高校要解决好如何提供具有参考和应用价值的数据的通性问题。
2 模型算法
文中所建立的交通网络设计模型是一个多目标优化问题.在求解此类问题时,多个目标之间可能会存在一定的对立,让多个目标同时达到最优是比较困难的,所以要协调各目标函数之间的关系,找到一系列能够使各个目标函数之间较好权衡的解的集合.文中采用粒子群优化算法对该模型进行求解.
算法流程如下:
(1)初始化粒子群,包括群体规模、每个粒子的位置和速度.每个粒子对应于该模型的决策变量即路段所增加的通行能力,粒子的初始位置随机产生.
(2)计算每个粒子的适应度值.由于文中的下层规划为常见的平衡配流问题,可以采用拉格朗日乘子法进行求解,并选择道路阻抗作为适应度函数.
(3)将每个粒子的适应度值和个体极值进行对比,如果适应度值大于个体极值Pbest,i(N),将个体极值替换为适应度值.
(4)将每个粒子的适应度值和全局极值进行对比,如果适应度值大于全局极值Gbest,i(N),将全局极值替换为适应度值.
(5)根据式(13)和(14)更新粒子的速度vi(N+1)和位置xi(N+1):
vi(N+1)=ωvi(N)+b1s1(Pbest,i(N)-xi(N))+
b2s2(Gbest,i(N)-xi(N))
(13)
xi(N+1)=xi(N)+vi(N)
(14)
式中,b1、b2为加速系数,s1、s2为[0,1]范围内变化的随机数,N为当前迭代次数.
(6)如果满足结束条件(误差足够低或到达最大循环次数),则退出,否则返回(2),进行循环迭代.
一般情况下,种群规模过小会缩小采样点的范围,导致算法性能下降;规模过大可以扩大采样点的选择,阻止早熟收敛的发生,但会使计算量和收敛时间大大增加.所以种群规模一般设为100~1 000,惯性权重采用非线性递减的策略进行动态调整[16],其变化如式(15)所示:
(15)
式中:Nmax为最大迭代次数;σmax、σmin分别为初始惯性权值和进化到最大代数的惯性权值;u和v为调整因子,取值范围分别为10 采用广州市天河区某路网验证上述交通网络设计双层规划模型的有效性,该交通网络由金穗路、花城大道、临江大道、冼村路、猎德大道、马场路6条道路构成,交通网络如图1所示. 图1所示的交通网络是集政治、经济、文化和对外交通功能以及商业、生活于一体的综合区域,位于广州市新城市中心区——天河区珠江新城,区域内各种交通资源高度聚集,拥有地铁、快速公交系统(BRT)等多层次城市交通体系,交通状况复杂,高峰时段交通拥堵情况较为突出,具有一定的改善需求. 图1 交通网络图 该交通网络由24条路段和9个节点组成,其中图1(a)中道路和图1(b)中路段的对应关系如表1所示. 表1 交通网络路段性质 图1(a)中金穗路与冼村路、猎德大道、马场路相交的交叉口分别为图1(b)中的节点1、4、7;花城大道与冼村路、猎德大道、马场路相交的交叉口分别为图1(b)中的节点2、5、8;临江大道与冼村路、猎德大道、马场路相交的交叉口分别为图1(b)中的节点3、6、9. 表2 交通网络基础数据 文中选择种群规模为100.算法的收敛性是靠迭代次数来保证的,综合考虑运算的速度,取迭代次数为500.加速系数b1和b2用于调整粒子的自身经验和社会经验在其搜索运动中所起的作用,设置较大或较小都不利于粒子的搜索,一般设置b1=b2∈[1,2.5],文中选取算法中最常见的设定,即b1=b2=2[17]. 图2 目标函数值随θ的变化 图3描述了上层规划值的收敛随迭代次数的变化情况.前60次迭代中,函数值随着迭代次数的增加而迅速降低,在将近180次迭代时基本趋于平稳,达到最优值94.3,最后迭代次数满足设置的迭代要求,达到最大允许迭代次数. 基于用户均衡配流连续性交通网络设计模型得出的设计方案[18]与文中模型的设计方案所得结果如表3所示. 表3 两种优化模型路段通行能力增加值1) 为了检验采用文中模型进行优化后的交通网络系统是否得到改善,利用道路服务水平指标——饱和度,将采用文中模型进行的交通网络设计前后的饱和度以及采用用户均衡模型进行改进后的路段饱和度进行对比,结果见表4. 表4 路段饱和度对比 从表4中可以看出:设计前有66.7%的路段饱和度在0.9以上,这一比例的路段服务等级均为E级及以下,说明该交通网络中重度拥堵以上的路段占66.7%,甚至有45.8%的路段处于严重拥堵状态,这种服务等级的交通网络急需改善;同时,经双层规划模型设计后,网络整体饱和度大大降低,只有25.0%的路段饱和度保持在0.9以上,其余路段的服务等级均处于D级以上,虽然有些路段的饱和度有一定程度的增加,但增加后的饱和度依然处于可接受范围内;采用基于用户均衡配流的连续性交通网络模型设计后,网络整体饱和度较设计前虽然有所下降,但仍有54.1%的路段饱和度在0.9以上.综上,文中提出的基于随机用户均衡配流的双层规划模型能够保证路段在被充分利用的同时保持相对的畅通,具有较好的优化设计效果. 文中建立了基于随机用户均衡配流的双层规划模型,该模型综合考虑了交通决策中交通出行者出行行为的差别性,反映了交通网络连接水平的路网可达性.节点作为交通网络的核心元素之一,对交通网络中的流量分布、出行成本及效率有重要的影响,因此文中将节点重要度作为描述节点功能的特征参数,引入到路网可达性的计算中.该模型中,上层规划模型引用道路走行时间作为适应度函数,设计了粒子群优化算法,下层规划运用拉格朗日乘子法进行计算. 选取道路饱和度对设计后的交通网络进行实例验证,将文中模型得到的所有路段平均饱和度与用户均衡模型得到的所有路段平均饱和度进行比较,结果表明,文中模型可使网络中的路段平均饱和度降低28.4%;与基于用户均衡配流的连续性交通网络设计模型相比,文中模型既可以提高交通网络中的道路利用率,又可以在一定程度上缓解拥堵问题.文中提出的双层规划模型只验证了对于连续型网络设计的可行性,在今后的研究中应对模型进行改进,使其对于离散型网络设计同样适用,同时,还应对其算法进行优化,使优化结果更接近实际情况. : [1] SUN Zhichen.Continuous transportation network design problem based on bi-level programming model [J].Procedia Engineering,2016,137:277- 282. [2] TONG Lu,ZHOU Xuesong,MILLER Harvey J.Transportation network design for maximizing space-time accessibility [J].Transportation Research Part B:Methodological,2015,81:555- 576. [3] YAO Baozhen,HU Ping,LU Xiaohong,et al.Transit network design based on travel time reliability [J].Transportation Research Part C:Emerging Technologies,2014,43:233- 248. [4] UNNIKRISHNAN Avinash,LIN Dun-Ying.User equili-brium with recourse:continuous network design problem [J].Computer-Aided Civil and Infrastructure Engineering,2012,27(7):512- 524. [5] 刘慧,杨超,杨珺.具有遗憾值约束的鲁棒性交通网络设计模型研究 [J].交通运输系统工程与信息,2013,13(5):86- 92. LIU Hui,YANG Chao,YANG Jun.Robust transportation network design modeling with regret value [J].Journal of Transportation Systems Engineering and Information Technology,2013,13(5):86- 92. [6] CHEN Anthony,ZHOU Zhong,CHOOTINAN Piya,et al.Transport network design problem under uncertainty:a review and new developments [J].Transport Reviews,2011,31(6):743- 768. [7] WANG Hua,LAM William H K,ZHANG Xiaoning,et al.Sustainable transportation network design with stochastic demands and chance constraints [J].International Journal of Sustainable Transportation,2015,9(2):126- 144. [8] 孙飞,龙建成.考虑速度限制的连续交通网络设计问题 [J].交通运输系统工程与信息,2015,15(3):146- 151. SUN Fei,LONG Jian-cheng.A continuous transportation network design problem with considering of speed limit [J].Journal of Transportation Systems Engineering and Information Technology,2015,15(3):146- 151. [9] LIU Chengliang,YU Ruilin.Spatial accessibility of road network in Wuhan metropolitan area based on spatial syntax [J].Journal of Geographic Information System,2012,4(4):128- 135. [10] 王炜,张桂红.城市道路路阻函数研究 [J].重庆交通大学学报(自然科学版),1992,11(3):84- 92. WANG Wei,ZHANG Guihong.Research on impedance function of urban streets [J].Journal of Chongqing Jiaotong Institute,1992,11(3):84- 92. [11] 叶春森,汪传雷,刘宏伟.网络节点重要度评价方法研究 [J].统计与决策,2010(1):22- 24. YE Chun-sen,WANG Chuan-lei,LIU Hong-wei.Research on evaluation method of network node importance [J].Statistics & Decision,2010(1):22- 24. [12] 张波,隽志才,林徐勋.基于累积前景理论的随机用户均衡交通分配模型 [J].西南交通大学学报,2011,46(5):868- 874. ZHANG Bo,JUAN Zhicai,LIN Xuxun.Stochastic user equilibrium model based on cumulative prospect theory [J].Journal of Southwest Jiaotong University,2011,46(5):868- 874. [13] LUCE R Duncan.Individual choice behavior [M].New York:John Wiley and Sons,1959. [14] FISK C.Some developments in equilibrium traffic assignment [J].Transportation Research B,1980,14(3):243- 255. [15] BELL M G H.Stochastic user equilibrium assignment and iterative balancing [C]∥Proceedings of the 12th International Symposium on Traffic and Transportation Theory.Berkeley:[s.n.],1993. [16] 罗金炎.粒子群优化算法惯性权重的一种动态调整策略 [J].沈阳化工大学学报,2013,27(4):371- 375. LUO Jin-yan.A dynamic adjustment strategy of inertia weight in particle swarm optimization [J].Journal of Shenyang University of Chemical Technology,2013,27(4):371- 375. [17] WANG Hei-Chia,YANG Che-Tsung.Enhanced particle swarm optimization with self-adaptation based on fitness-weighted acceleration coefficients [J].Intelligent Automation & Soft Computing,2015,22(1):1- 14. [18] XU Tianze,WEI Heng,WANG Zhuan-De.Study on continuous network design problem using simulated annealing and genetic algorithm [J].Expert Systems with Applications:An International Journal,2009,36(2):2735- 2741.3 实例分析
3.1 交通网络概况
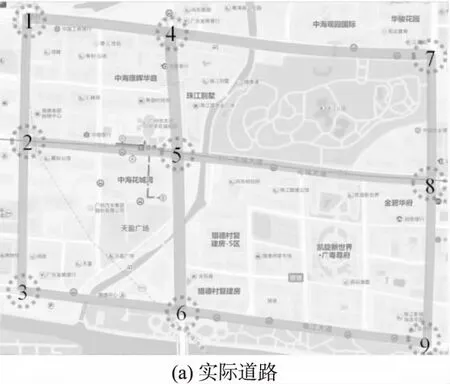

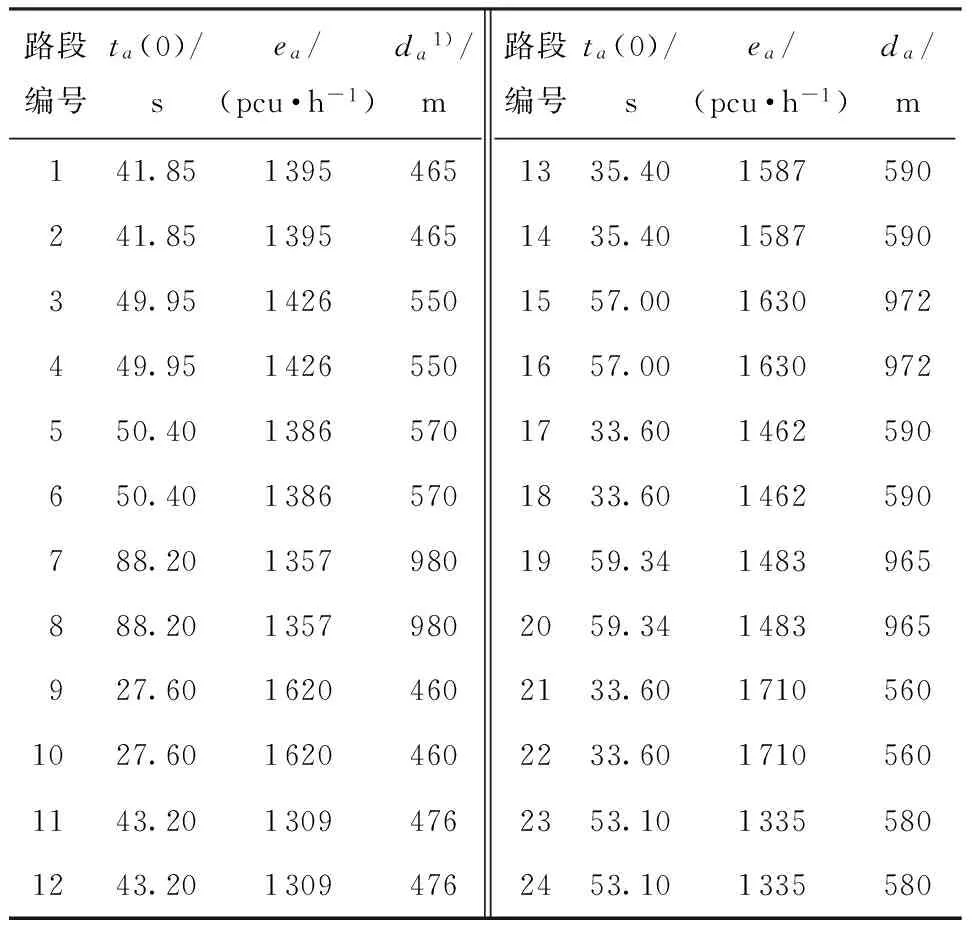
3.2 计算结果与分析
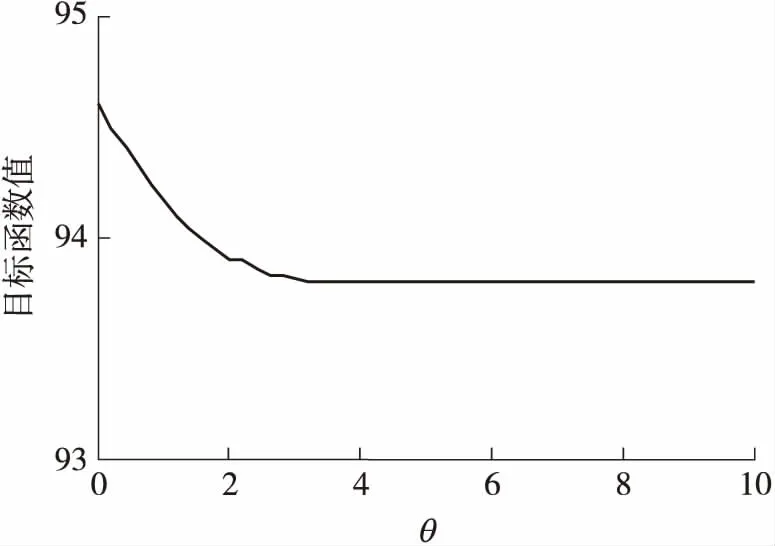
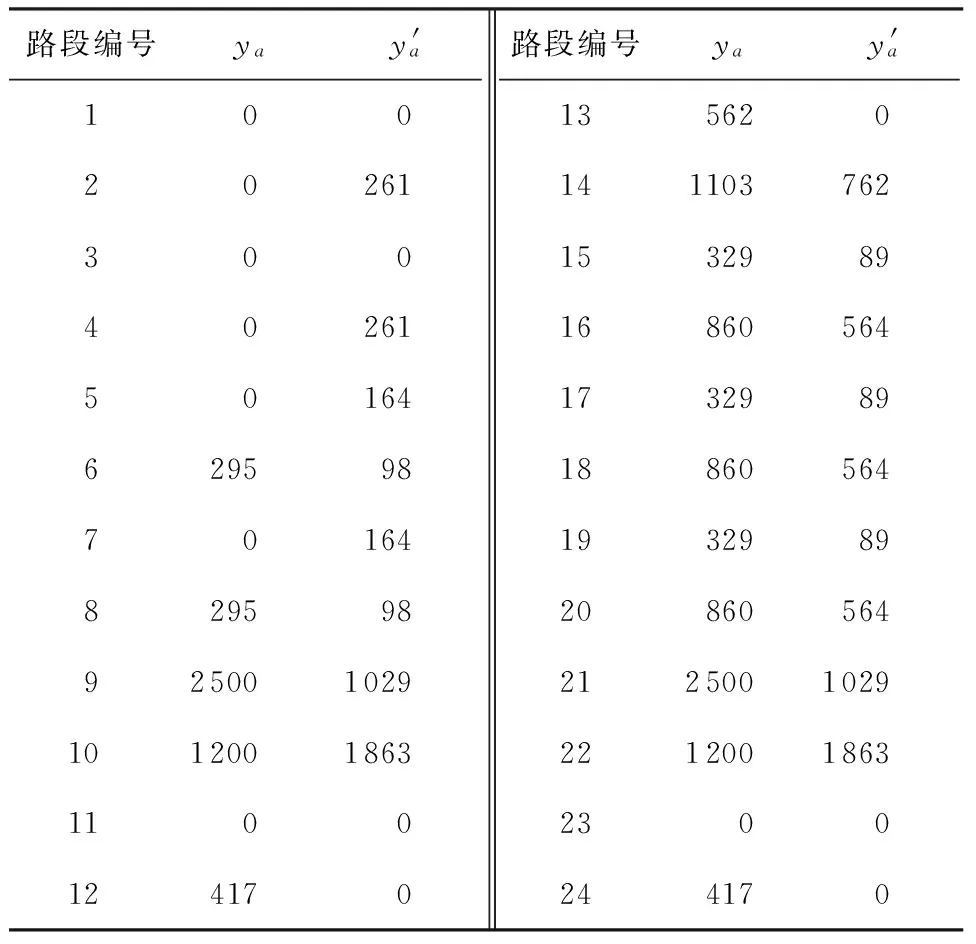
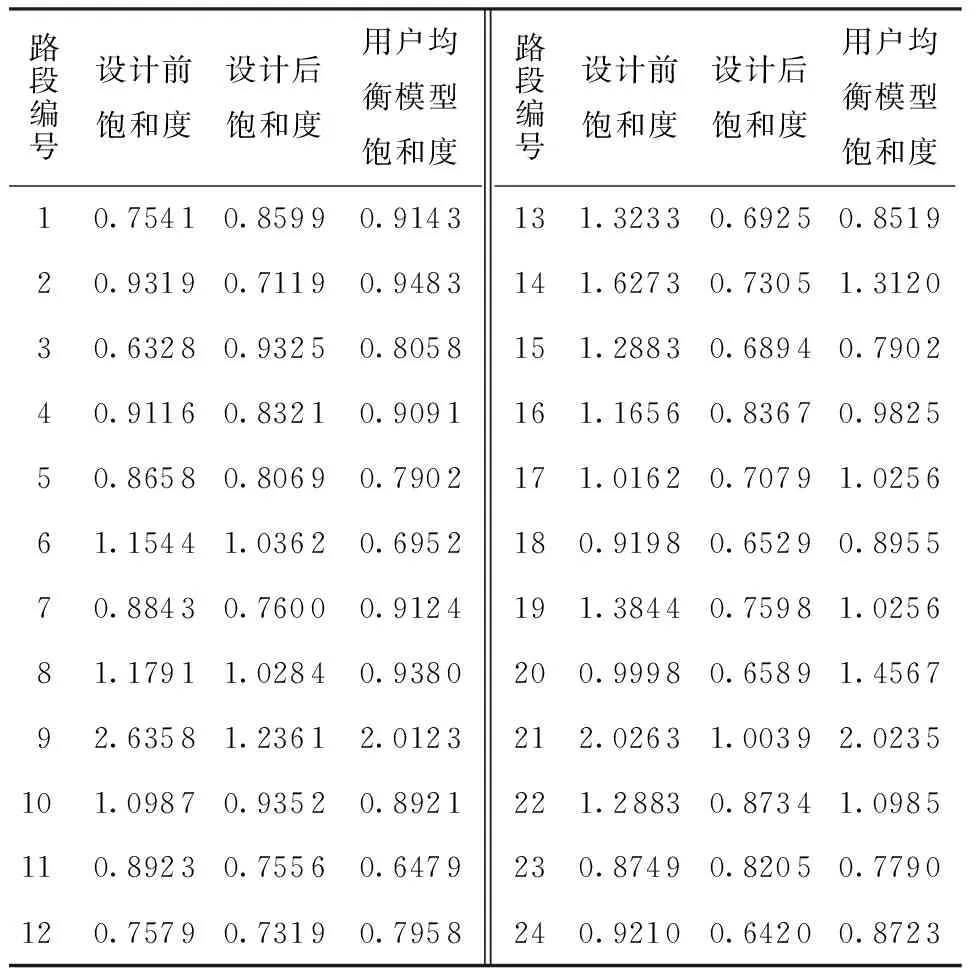
4 结语

