基于拉普拉斯变换的路面一维时变温度场预测*
张丽娟 黄建武 许薛军
(1.华南理工大学 土木与交通学院, 广东 广州 510640; 2.广东省公路管理局, 广东 广州 510075)
路面温度场是路面结构分析设计中非常重要的影响因素,关于路面温度场的理论求解方法有很多种,主要包括分离变量法、积分变换法和拉普拉斯变换法等.
Barber[1]首先采用半无限表面介质温度周期变化时热传导方程的解来确定路面最高温度.严作人[2]采用较简单的三角函数(或级数)来表示气温、太阳辐射等气候条件,推导出一维层状路面体系周期性温度场的解析解.吴赣昌[3]得出了二维层状体系温度场分布的解析解.韩子东[4]建立了一维路面结构温度场数学模型,采用分离变量法求解温度场的解析解.Chong等[5]通过拉普拉斯变换及数值反演的方法求解了一维双层路面结构体系温度场的解析解.Dong等[6- 7]采用拉普拉斯变换法及数值反演方法先后建立了柱坐标下沥青路面周期性温度场的解析解及n层刚性路面体系一维温度场的解析解.吴建良等[8]得到了路面非周期一维温度场的傅里叶级数解.秦勃[9]利用积分变换法求解热传导微分方程,得到了路面结构时变温度场的解析解.
分离变量法和积分变换法广泛应用于求解路面温度场的解析解,其计算模型的理论推导较为完整,但理论分析过程比较复杂,且需对计算公式进行多次简化,使得计算精度稍差.拉普拉斯变换法由傅里叶变换法发展而来,可以将关于时间变量的偏导数从微分方程中去除,大大简化了求解过程;虽然逆变换相对复杂,很多情况下不能直接表示,但可以采用数值反演的方式进行替代,可操作性较强,且其预测精度完全可以满足工程的要求,便于工程应用.因此,文中采用拉普拉斯变换及数值反演的方法,推导一种多层路面体系的一维时变温度场解析解.
1 一维时变温度场数学模型
1.1 导热方程
设n层路面结构体系的一维时变温度函数为Tj(z,t)(℃),其表示路面结构内部温度随深度z和时间t的变化情况,下标j表示层位序号.假设路面结构为各向同性的均质体,各层材料的热物性参数不随温度变化.
忽略路面水平方向的热传导,一维时变温度场导热方程为
(1)
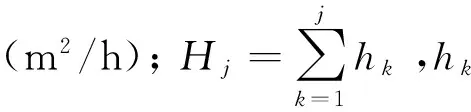
1.2 层间接触条件
由于层与层之间接触紧密,因此假定温度和热流在层间连续,即
Tj(Hj,t)=Tj+1(Hj,t)
(2)
(3)
式中,λj为导热系数(W·m-1·K-1).
1.3 温度场限值
设各结构层随时间、深度变化的温度上限是一个常数V(℃),即
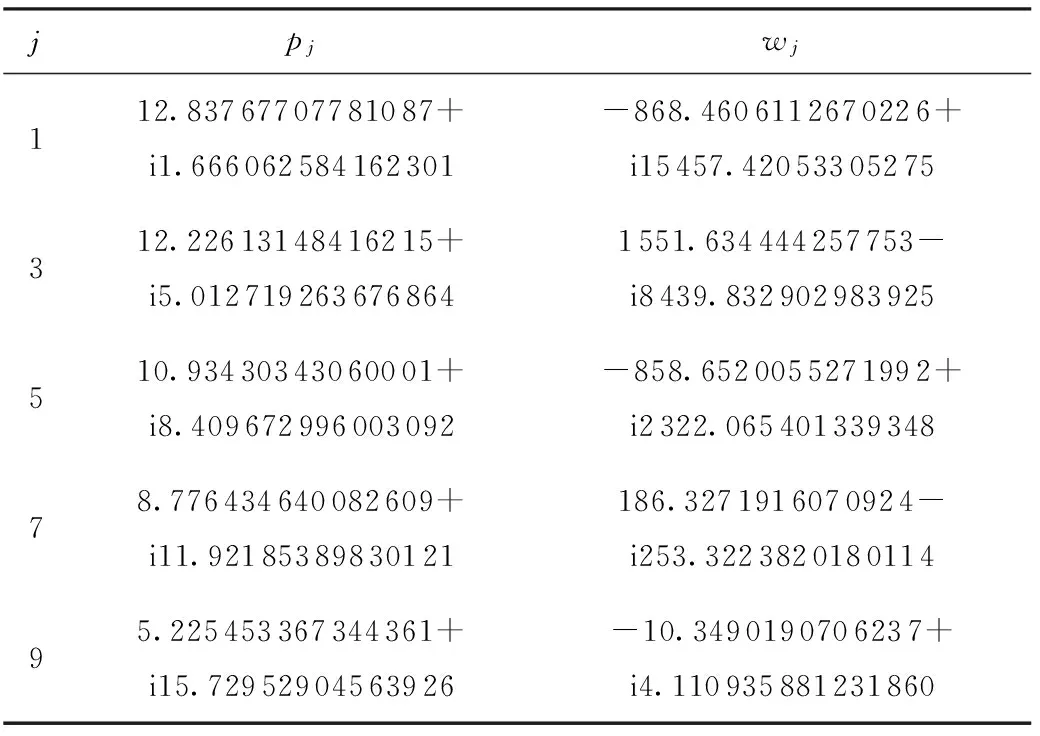
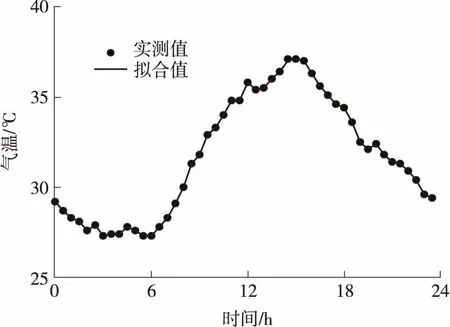
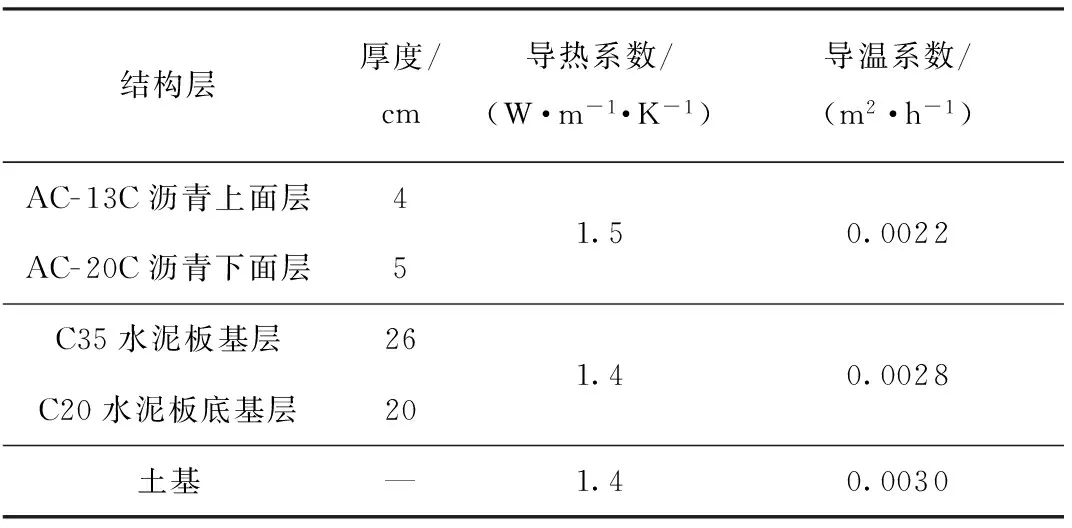
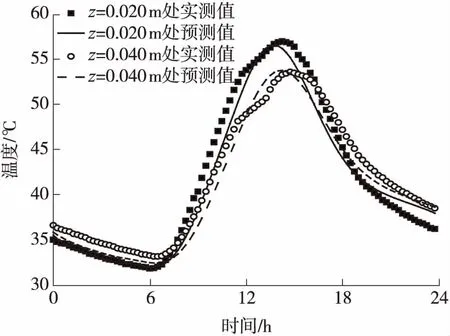
|Tj(z,t)| (4) 路面结构长期暴露在自然环境之中,经受周期变化的气候条件影响.求解一维路面温度场时,须将气温Ta(t)的变化曲线和太阳辐射强度Q(t)的变化曲线进行数学处理后输入到路面结抅温度场的预估模型中去. 应用基于最小二乘近似的内插三角函数多项式拟合气温和太阳辐射强度的变化曲线[10]: (5) (6) 当l=0,1,2,…,2m-1时,Tl、Ql分别为t=lte/(2m)时的气温和太阳辐射强度实测值. 路表与周围环境之间的能量平衡方程为 (7) 以上各式中,Q(t)为太阳辐射强度(W/m2),Ta(t)为气温(℃),T1(0,t)为路表温度(℃),μ为路面材料对流换热系数(W·m-2·K-1),γ为考虑路面本身向外辐射能量后的路面有效太阳能吸收率. 将式(5)和(6)代入式(7),可以得出 (8) 式(1)-(4)和式(8)共同构成了基于实测气温和太阳辐射强度的路面一维时变温度场预测数学模型. 为简化计算,假定各路面结构层初始温度相同且为一常量,即当t=0时, Tj(z,0)=G (9) 式中,G是常量. 采用拉普拉斯变换法求解一维时变温度场数学模型.引入变量θj(z,t): θj(z,t)=Tj(z,t)-Tj(z,0) (10) 式中,j=1,2,…,n. 式(1)-(4)和式(8)所建立的数学模型可转化为 (11) θj(Hj,t)=θj+1(Hj,t) (12) (13) |θj(z,t)| (14) (15) θj(z,0)=0,j=1,2,…,n (16) 利用变换后的数学模型并考虑实测气温和太阳辐射强度,可以求解路面一维温度场. (17) 对层间接触条件(即式(12)和(13))进行拉普拉斯变换,得 (18) (19) 此外,由式(18)和(19)可以推导出Aj、Bj(j=2,3,…,n)与A1、B1的关系 (20) (21) 当j=2,3,…,n-1时, 由式(17)可知,对于n层路面结构体系,总共有2n个积分常量Aj、Bj(j=1,2,…,n),它们可通过对边界条件和层间接触条件进行拉普拉斯变换得到. 由式(14)的温度场限值假设,可知Bn(s)=0.再由式(21),得 (22) 式(15)经拉普拉斯变换后,与式(22)联立,可求得A1、B1如下: 式中: (23) 式中:ν为衰减指数;i是虚数,i2=-1. (24) 式中,pj和wj(j=1,2,…,10)分别代表高斯积分点和权重系数. 表1给出了10节点的高斯积分点和权重系数.j=2,4,6,8,10时的pj、wj值分别为j=1,3,5,7,9时的共轭复数[12]. 令st=p,式(23)变换为 (25) (26) 最后将式(9)和(26)代入式(10),得出各层路面结构的温度为 Tj(z,t)=θj(z,t)+G (27) 表1 高斯积分点pj和权重系数wj 3.1.1 气温和太阳辐射 利用基于最小二乘近似的内插三角函数多项式,采用1stOpt曲线拟合软件拟合随时间变化的气温和太阳辐射强度,得出式(5)、(6)中气温和太阳辐射强度的相关参数值.以天为周期、30 min为间隔(即m=24),对广东省佛山市某旧水泥路面加铺沥青层路面结构在2015年8月24日(夏季)和2015年12月16日(冬季)的气温、太阳辐射强度的实测与拟合结果进行对比,结果如图1-4所示. 图1 气温实测值与拟合结果(2015年8月24日) 3.1.2 路面空气对流 路面表面与空气之间存在对流换热,在实际工程应用中,对流换热系数主要受风速影响,通常采用近似值代替,可以采用下列经验公式计算对流换热系数[13]: μ≈9.4+3.7v (28) 式中,v为一天的平均风速(m/s). 广东省佛山市某旧水泥路面加铺沥青层路面结构在2015年8月24日和2015年12月16日的日平均风速分别为0.48和1.09 m/s,计算得到的对流换热系数分别为11.2和13.5 W/(m2·K). 广东省佛山市某旧水泥路面加铺沥青层路面结构组成及其厚度如表2所示.在验证温度场数学模型时,将该路面结构假设为三层路面结构体系:第1层为沥青混凝土层,厚度为9 cm;第2层为水泥混凝土层,厚度为46 cm;第3层为路基,厚度为无限大.参考文献[14]中的取值选取各层的材料热物理性能参数,列于表2.由于加铺层为沥青混凝土层,考虑路面本身向外辐射能量后的路面有效太阳能吸收率γ取为0.8. 表2 模型验证输入参数 利用Matlab软件编制温度场解析解计算程序,计算出各结构层的温度场数据.路面结构层温度从上向下逐渐趋于稳定,通过观察实测温度数据,2015年8月24日和2015年12月16日的路面结构层温度初值分别取为36和20 ℃.输入层厚、材料参数、实测空气温度和太阳辐射强度后,可以预测该旧水泥路面加铺沥青层路面结构体系中任一深度处的温度曲线. 选取该旧水泥路面加铺沥青层路面结构的上面层中(z=0.020 m)、上面层底(z=0.040 m)、下面层中(z=0.065 m)、下面层底(z=0.090 m)、C35水泥板基层底(z=0.350 m)、C20水泥板基层底(z=0.550 m)等不同路面结构深度,以天为周期、15 min为间隔,得到2015年8月24日(夏季)和2015年12月16日(冬季)路面结构层温度的实测值和理论预测值,分别如图5-10所示. 表3列出了温度场预测值Tp与实测值Tm偏差(Tp-Tm)的最大、最小值以及平均绝对偏差(|Tp-Tm|)值. 图5 z=0.020 m和z=0.040 m处预测温度和实测温度(2015年8月24日) 从图5-10、表3可以看出,采用基于拉普拉斯变换法的一维路面温度场理论预估的旧水泥路面加铺沥青层路面结构温度与实测温度之间的最大偏差在3 ℃以下,平均绝对偏差在1.6 ℃以下,可见该模型预测精度非常高.出现偏差的原因可能与模型的一些假设(如将路面结构内部初始温度设为常数)、参数的取值(如设路表对流换热系数在一天之内为常量)以及实测数据本身存在的误差等因素有关. 表3 不同深度处的路面温度预测值与实测值对比 文中采用热传导方程建立自然环境下一定周期内路面结构的一维时变温度场数学模型,将影响时变温度场的主要因素(即气温和太阳辐射强度)考虑为路表边界条件,应用基于最小二乘近似的内插三角函数多项式拟合一定时段内的气温和太阳辐射强度,据此确定温度场路表边界条件.将温度场数学模型进行拉普拉斯变换,推导出第j层和第1层的积分常量之间的关系,以简化求解过程;然后利用高斯积分公式进行拉普拉斯数值近似反演求解出路面结构温度场.利用Matlab软件编制温度场模型的计算程序,输入层厚、材料参数、实测气温和太阳辐射强度,可以预测路面结构体系中任意深度处的温度值.通过与旧水泥路面加铺沥青层路面结构实测温度场数据的对比发现,预测温度与实测温度之间的最大偏差在3 ℃以下,平均绝对偏差在1.6 ℃以下,表明提出的一维时变温度场解析解模型可以合理预测旧水泥路面加铺沥青层路面结构在冬季和夏季条件下以天为周期的路面结构温度场分布. 下一步将开展路面材料的热物性参数随气温、太阳辐射和风速等环境因素的变化规律研究,进一步完善温度场预测模型,研究路面温度场对高温车辙、低温开裂和疲劳破坏等路用性能的影响,为旧水泥路面加铺沥青层路面结构和材料设计提供参考. : [1] BARBER E S.Calculation of maximum pavement tempe-ratures from weather reports [J].Highway Research Board Bulletin,1957(168):1- 8. [2] 严作人.层状路面体系的温度场分析 [J].同济大学学报,1984(3):76- 85. YAN Zuo-ren.Temperature field of layered pavement [J].Journal of Tongji University,1984(3):76- 85. [3] 吴赣昌.层状路面体系温度场分析 [J].中国公路学报,1992,5(4):17- 25. WU Gan-chang.The analysis of pavement temperature field of multi-layer system [J].China Journal of Highway and Transport,1992,5(4):17- 25. [4] 韩子东.道路结构温度场研究 [D].西安:长安大学,2001. [5] WANG Chong,RAMONE Tramontini,LUCIANO Pivoto Specht.Application of the Laplace transform and its numerical inversion to temperature profile of a two-layer pavement under site condition [J].Numerical Heat Transfer,Part A:Applications,2009,55(11):1004- 1018. [6] WANG Dong,ROESLER Jeffery R,GUO Da-zhi.Analytical approach to predicting temperature fields in multila-yered pavement systems [J].Journal of Engineering Mechanics,2009,135(4):334- 344. [7] WANG Dong,ROESLER Jeffery R.One-dimensional rigid pavement temperature prediction using Laplace transformation [J].Journal of Transportation Engineering,2012,138(9):1171- 1177. [8] 吴建良,孙立军.路面非周期一维温度场的傅里叶级数解 [J].中国公路学报,2012,25(1):29- 34. WU Jian-liang,SUN Li-jun.Fourier series solution of non-periodic 1-D temperature field of pavement [J].China Journal of Highway and Transport,2012,25(1):29- 34. [9] 秦勃.路面结构时变温度场的解析解及预估模型 [D].杭州:浙江大学,2014. [10] BURDEN R L,FAIRES J D.Numerical analysis [M].7th Ed.Pacific Grove:Brooks/Cole,2001. [11] 胡汉平.热传导理论 [M].合肥:中国科学技术大学出版社,2010. [12] STROUD A H,SECREST D.Gaussian quadrature formulas [M].Upper Saddle River:Prentice Hall,1966. [13] 朱伯芳.大体积混凝土温度应力与温度控制 [M].北京:中国电力出版社,1998. [14] 资建民,王海军,李福宝,等.大粒径沥青混合料基层缓解反射裂缝应力分析 [J].华中科技大学学报(城市科学版),2006,23(Sup 1):8- 12. ZI Jian-min,WANG Hai-jun,LI Fu-bao,et al.Reflection cracking resistance stress analysis of large stone asphalt mixures base in asphalt pavement [J].Journal of Huazhong University of Science and Technology(Urban Science Edition),2006,23(Sup 1):8- 12.1.4 路表边界条件
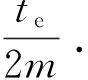
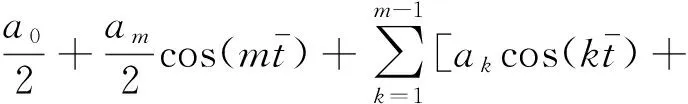
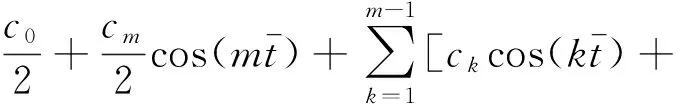
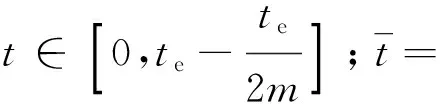
2 路面温度场求解
2.1 初始条件
2.2 模型转换
2.3 拉普拉斯变换
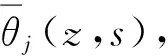
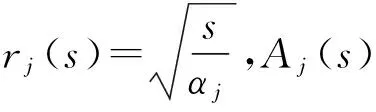
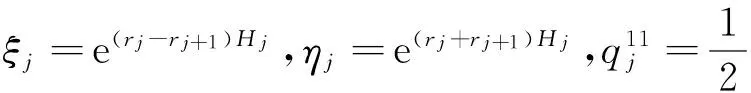
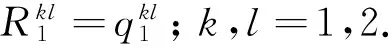
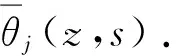
2.4 拉普拉斯数值反演
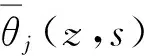
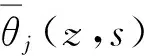
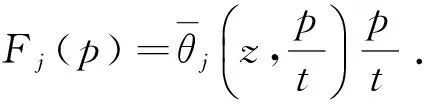
3 模型验证
3.1 温度场的外部环境
3.2 材料热物理性能参数
3.3 模型验证结果

4 结语

