浅海环境下界面对舰船水下标量电位的影响

陈夫余，陈 聪，李定国，冯亚敏

(海军工程大学理学院，湖北 武汉430033)

浅海环境下界面对舰船水下标量电位的影响

陈夫余，陈 聪，李定国，冯亚敏

(海军工程大学理学院，湖北 武汉430033)

针对目前平行分层界面对舰船水下电场的影响研究未进行量化分析的不足，提出以修正系数表征界面对标量电位分布影响的方法。该方法可以量化平行分层界面对标量电位产生的影响，通过研究界面修正系数与海洋水深、海水电导率、场源间距等因素的关系，可以藉此掌握这些因素对舰船水下标量电位分布的影响规律。仿真分析表明，界面修正系数随场源间距、海水电导率增大而增大，随海洋水深、海床电导率增大而减小，不同条件下存在不同的有效修正次数。采用修正系数和有效修正次数的概念，可以将无穷项求和的场分布表达式改写为有限项求和，降低场分布表达式的复杂程度，使其更易于在场源反演、深度换算等实际应用中运用。

舰船水下电场；修正系数；数值仿真；标量电位；界面

0 引言

舰船在海洋环境中，船体不同部位的异种金属会发生电偶腐蚀，为了抑制这种腐蚀，舰船一般安装有阴极保护系统。腐蚀和防腐电流会产生具有明显信号特征的电场，称为舰船水下电场[1-2]。舰船水下电场是舰船在海洋环境中的重要暴露源，以其为特征信号的水中兵器和水下探测技术给舰船生命力和战斗力带来严重威胁[3-4]。近年来相关研究表明，水平电偶极子是舰船水下电场的基本模拟单元，在涂层完好的情况下，水下舰船电场的主体可用位于螺旋桨处的水平直流电偶极子在空气-海水-海床三层模型中的场分布来模拟[5-8]。舰船在浅海环境中航行，其水下电场分布受空气-海水、海水-海床平行分层界面的影响显著。在已有的文献中，文献[9]在实验室环境下，控制场源距离不变，测得空气界面附近场点的标量电位是远离界面场点的1.4倍左右；文献[10]仿真分析表明，分层海洋环境下，海床和空气界面对水下电磁场的影响显著，且海床电导率越小，对电场的增强作用越明显。但上述文献只得出一些定性结论，未对界面的影响进行量化分析，对影响因素也未进行深入研究。本文针对此问题，提出以修正系数表征界面对场的影响，并采用数值仿真的方法，对海洋水深、电导率、场源间距等因素对界面修正系数的影响进行了分析。

1 浅海环境下舰船水下电场的偶极子模型

浅海环境可视为空气-海水-海床三层平行分层媒质空间。建立如图1所示直角坐标系。取水平面为(xOy平面，z轴垂直于水面且指向地心。空气、海水、海床三种介质分别均匀，电导率、磁导率、电容率分别表示为σi，μi，εi，i= 0, 1, 2，其中磁导率μ0=μ1=μ2。海水深度为D，z<0区域为空气， 0D区域为海床。设舰船水下电场的等效水平直流电偶极子Idl=Ixdli位于海水中的(x0,y0,z0)处。

采用镜像法推导上述水平直流电偶极子在海水空间中产生的标量电位。在场点(x,y,z)处所产生的标量电位可表示为场源及其通过上下界面分别形成的无数镜像电偶极子在无限大海水空间中产生的标量电位的叠加[11]，镜像电偶极子的场体现了界面对场的影响。

(1)

2 界面修正系数的引入

2.1 界面修正系数的定义

为更清楚看出式(1)中各项的物理意义，可以将式(1)中的无穷项分为三部分，一是场源在无限大海水域形成的场，二是空气界面以上镜像电偶极子形成的场，三是海床界面以下镜像电偶极子形成的场，因此可将式(1)改写为：

(2)

其中，ΦS表示场源在无限大海水域中产生的标量电位。

(3)

ΦDM表示场源在海水-海床界面之下所成的像在无限大海水域中产生的标量电位。

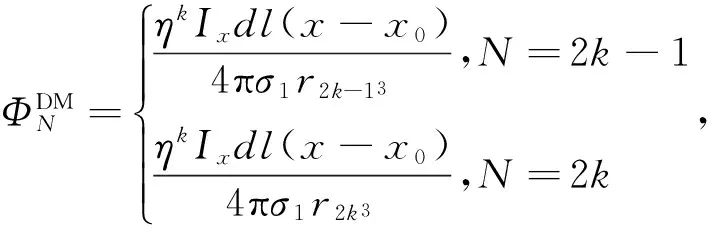
(4)

ΦUM表示场源在空气-海水界面之上所成的像在无限大海水域中产生的标量电位；

(5)

由式(2)可见，各镜像偶极子的标量电位ΦDM，ΦUM可视为是对场源在无限大海水域中产生的标量电位ΦS的修正。镜像偶极子因界面而产生，因此ΦDM，ΦUM分别表示因上、下界面的存在而对标量电位分布产生的影响。为定量分析分层界面对场的影响，可引入修正系数ξM，为镜像偶极子与场源在全空间海水域中产生的标量电位的比值。定义如下：

上界面的第N级修正系数，即上界面对场的第N级修正效果表示为：

(7)

因此式(2)可改写为：

(8)

由ξM定义及ΦDM，ΦUM，ΦS表达式可见：修正系数与海洋环境电导率分布、海水深度、场源点间距及镜像次数有关，因此有必要研究上述各因素对修正系数的影响规律，从而掌握分层海洋环境界面对场的影响规律。

2.2 有效修正次数的定义

由ξM定义及ΦDM，ΦUM，ΦS表达式可看出，修正系数ξM<1；且随着N的增大单调减小，因此在一定精度要求下，存在一个有效修正次数Neff，也就是经过Neff次求和，即可获得满足精度要求的标量电位。假设前Neff次镜像电偶极子产生的修正能达到标量电位的修正精度d，则定义前Neff次修正为有效修正，Neff次以后的镜像电偶极子产生的修正很小，可以略掉不计。

由式(8)展开可得：

(9)

简单分析可知，场点距离源点较远时，上式中源点和各镜像电偶极子与场点距离大致相等，则位于较远处的场点其标量电位表达式可改写为：

Φ(x,y,z)=

(10)

显然上式为几何级数，在η<1，即海床电导率不等于0时具有收敛性，此时有效修正次数可求，表达式如下：

(11)

3 仿真分析

为掌握分层海洋环境界面对舰船水下标量电位影响的规律和特征，现以海水中水平电偶极子模拟舰船，采用数值计算的方法对镜像次数、海洋环境电导率、海水深度、场源点间距对修正系数的影响进行分析。下文参数设定均基于实际海洋环境。

假设舰船等效水平直流电偶极子位于(0 m, 0 m, 15 m)处，等效偶极距为1 A·m。

3.1 镜像次数对修正系数的影响

取海水电导率σ1为4 S/m，海床电导率σ2为0.4 S/m，海洋水深D为30 m。取靠近海水-空气分界面的场点(50 m, 10 m, 5 m)、位于海水中部的场点(50 m, 10 m, 15 m)、靠近海水-海床分界面的场点(50 m, 10 m, 25 m)。分别计算上述三个场点上界面和下界面镜像电偶极子修正系数随镜像次数的变化，仿真结果如图2所示。

由图2可知，1)随着镜像次数的增加，上界面和下界面的修正系数均迅速减小。修正系数的减小，来源于两方面，一是随镜像次数增加，镜像电偶极子的偶极矩量值变小；二是镜像次数增加，镜像电偶极子位置变化，到场点距离变大。2)图2 (a)中修正系数最大的场点是(50 m, 10 m, 5 m)，图2(b)中修正系数最大的场点是(50 m, 10 m, 25 m)。说明场点位置越靠近界面，其电位受界面影响越大。

图2 上下界面修正系数随镜像次数的变化Fig.2 Correction factor varies with the time of mirror image

3.2 海洋水深对修正系数的影响

取海水电导率σ1为4 S/m，海床电导率σ2为0.4 S/m。针对位于(50 m, 10 m, 20 m)处的场点，分别计算上下界面前三个镜像电偶极子的修正系数随海洋水深的变化，仿真计算结果如图3所示。

由图3可知，1)随海洋深度D的增加，相同级次的修正系数均减小，表明海洋水深越深，镜像电偶极子产生的修正电位越小，即界面对标量电位的分布影响越小；且海洋水深较小时，各镜像电偶极子修正系数，即对场的贡献有明显不同，第一个镜像电偶极子产生的修正明显大于第二个和第三个镜像电偶极子，而当海洋水深较大时，除上界面第一个镜像电偶极子，其他镜像电偶极子的修正系数趋于0，表明此时只有上界面对场有影响，此时相当于深海情形。2)上界面第一级修正系数保持不变。这一点由ξM，ΦUM，ΦS的定义表达式可以得到解释，上界面第一级修正系数与海洋水深无关。

3.3 场源间距对修正系数的影响

取海水电导率σ1为4 S/m，海床电导率σ2为0.4 S/m，海洋水深D为30 m。固定场点的y=10 m，z=20 m，x坐标变化。仿真计算场点位置不同时，上下界面前三个镜像电偶极子修正系数随x的变化，仿真结果如图4所示。

由图4可知，场点x值越小，即场点离源点距离越近时，源直接产生的场占主体成分，镜像电偶极子产生的修正是次要的，场点x值越大，即场点源点距离越远时，镜像电偶极子的修正效果越明显，即界面对标量电位分布的影响越大。场点距源点较近时，各镜像电偶极子修正系数同时受距离和偶极矩量值影响，且二者影响都比较大。当场点距源点较远时，各镜像电偶极子与场点距离差别不大，修正系数的差别主要来源于电偶极矩量值的变化。

3.4 电导率对修正系数的影响

1)海床电导率

取海水电导率σ1为4 S/m，海床电导率变化，海洋水深D为30 m。考虑位于(50 m, 10 m, 20 m)处的场点，仿真计算海床电导率不同时，上下界面前三个镜像电偶极子修正系数随海床电导率的变化，仿真结果如图5所示。

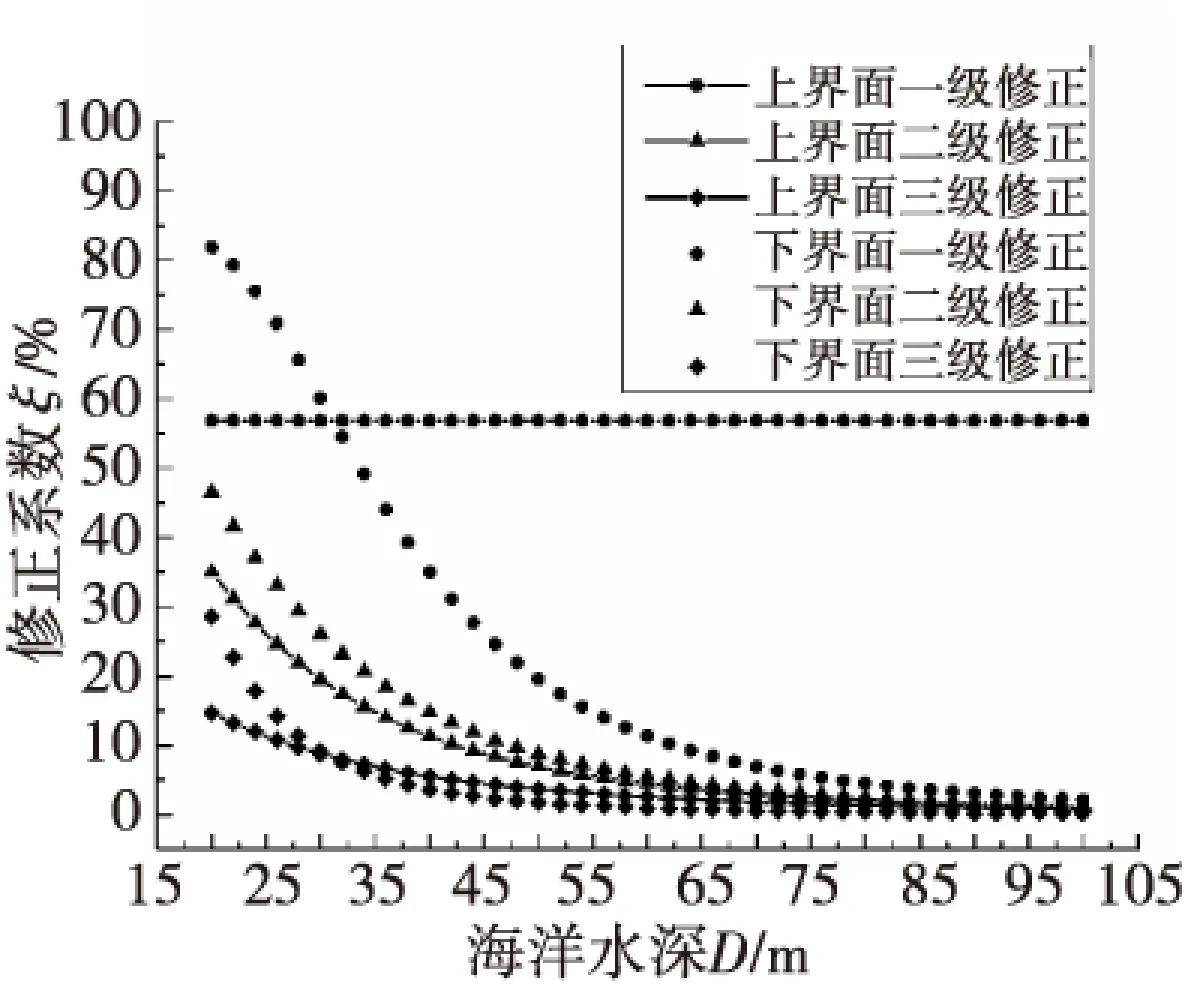
图3 修正系数随海洋水深的变化Fig.3 Correction factor varies with the depth

图4 修正系数随x值的变化Fig.4 Correction factor varies with x

图5 修正系数随海床电导率的变化Fig.5 Correction factor varies with the sea bed conductivity

由图5可知，1)海床电导率越大，相同级次的修正系数越小，说明海床电导率越大，镜像电偶极子的修正电位越小，即界面对标量电位分布的影响越小。其原因为海床电导率越大，η值越小，即镜像电偶极子量值越小。2)上界面第一级修正系数不受海床电导率变化的影响。

2)海水电导率

取海床电导率σ2为0.4 S/m，其他参数同上，计算海水电导率变化时，上下界面前三个镜像电偶极子修正系数随海水电导率的变化，仿真结果如图6所示。

由图6可知，1)海水电导率越大，相同级次的修正系数越大，说明海水电导率越大，镜像电偶极子的修正电位越大，即界面对标量电位分布的影响越大。其原因为海水电导率越大，η值越大，即镜像电偶极子量值越大。2)上界面第一级修正系数不受海水电导率变化的影响。

3.5 有效修正次数仿真分析

下面通过一个仿真算例来分析有效修正次数Neff。取海水电导率σ1为4 S/m，海床电导率σ2为0.4 S/m。假设无穷远处场点标量电位修正精度d要求达到95%，则采用式(11)计算可得需要镜像电偶极子个数为28，即有效修正次数Neff为28。仿真计算无穷项电偶极子(上下界面各镜像1 000次)和有效修正次数Neff项电偶极子电位分别随x,y的变化，如图7、图8所示。可见有效修正次数镜像电偶极子产生的电位和无穷项镜像电偶极子产生的电位基本重合，计算其在本区域内的相对均方误差，图7相对均方误差低至1.35 × 10-4，图8相对均方误差低至2.60 × 10-4，可知在计算浅海分层环境下舰船水下电场时，只计算有限几项有效修正，就可以与无穷镜像电偶极子的计算精度相比拟。

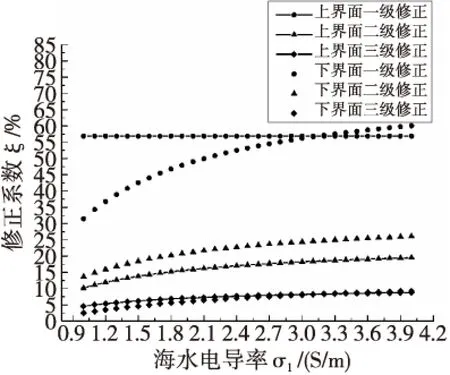
图6 修正系数随海水电导率的变化Fig.6 Correction factor varies with the sea water conductivity

图7 电位随x的变化Fig.7 Variation of electric scalar potential with x

4 结论

本文提出了以界面修正系数表征平行界面对舰船水下标量电位的影响。该方法可以量化平行分层界面对舰船水下电场标量电位产生的影响，通过研究界面修正系数与海洋水深、海水电导率、场源间距等因素的关系，可以藉此掌握这些因素对舰船水下标量电位分布的影响规律。仿真结果表明，界面修正系数随场源间距、海水电导率增大而增大，随海洋水深、海床电导率增大而减小，不同条件下存在不同的有效修正次数。采用修正系数和有效修正次数的概念，可以将无穷项求和的场分布表达式改写为有限项求和，降低场分布表达式的复杂程度，使其更易于在场源反演、深度换算等实际应用中运用。

[1]AdeyR,BaynhamJ.PredictingcorrosionrelatedelectricalandmagneticfieldsusingBEM[C]//Conf.Proc.UDTEurope，2000：473.

[2]RodrigoFJ,María-DoloresB,SánchezA.Underwaterthreatsdetectionbasedonelectricfieldinfluences[C]//UnderseaDefenceTechnologyConferenceEurope,Hamburg,Germany.2010:1-6.

[3]BirsanM.Measurementoftheextremelylowfrequency(ELF)magneticfieldemissionfromaship[J].MeasurementScienceandTechnology,2011,22(8):085709.

[4]AllanPJ.Investigationsofthemagneticfieldsfromshipsduecorrosionanditscountermeasures[D].Glasgow:UniversityofGlasgow, 2004:101-116．

[5] 胡英娣,龚沈光,闫永贵.船舶静态电场混合模型的逐步回归法优化求解[J].探测与控制学报，2013,35(4):32-35.

[6]RawlinsPG.Aspectsofcorrosionrelatedmagnetic(CRM)signaturemanagement[C]//Conf.Proc.UDTEurope, 1998: 237-242．

[7] 熊露,毕晓文,张伽伟.船舶金属螺旋桨旋转产生的涡旋电场模型[J].探测与控制学报，2016,38(2):57-63.

[8]AllanPJ.Investigationsofthemagneticfieldsfromshipsduetocorrosionanditscountermeasures[D].Glasgow:UniversityofGlasgow,2004.

[9] 罗晓强,陈聪,陈勇.舰船水下标量电位分布特征研究[J].武汉理工大学学报，2012, 34(11): 48-52.

[10] 陈聪,蒋治国,姚陆锋,等.分层海洋环境对潜艇腐蚀相关静态电磁信号的影响研究[J].武汉理工大学学报(交通科学与工程版)，2014,38(5):950-954.

[11] 陈聪,李定国,蒋治国等.二次等效法求三层媒质中静态电偶极子的场分布[J].物理学报，2012, 61(24):1-6.

The Influence of Shallow Sea Interface to the Underwater Electric Field

CHEN Fuyu，CHEN Cong，LI Dingguo，FENG Yamin

(College of Sciences, Navy University of Engineering, Wuhan 430033, China)

Aiming at the problem that the present research on the influence of the parallel layer interface to the underwater electric field of ships was not quantified, a correction factor was introduced to represent the influence on the electric scalar potential of the interface. This method was able to quantify the influence. The influence of these factors on the distribution of the underwater scalar potential of the ship could be obtained by considering the relationship between the interface correction factor and the water depth, the conductivity of the sea water and the distance between the electric dipole and field point. Numerical simulation results showed that the correction factor would increase along with the increase of the distance between the electric dipole and field point, the increase of sea water conductivity, and would decrease with the increase of the water depth and the seabed conductivity. The correction factor and effective correction times were introduced to change the field distribution expression of infinite items summation into finite items summation, and reduce the complexity of field distribution expression. Therefore, it was easier to apply in practical application, such as field source inversion and extrapolation of the static electric field etc.

underwater electric field; correction factor; numerical simulate m; electric scalar potential; interface

2016-11-21

国家自然科学基金项目资助(51109215)；国防预研基金项目资助(51444070105JB11)

陈夫余(1991— ), 男，山东临沂人，硕士研究生，研究方向：电磁目标特性。E-mail:chfuyu@163.com。

TJ6

A

1008-1194(2017)02-0029-05