最优区域划分的飞行器视觉测量标记
姜 威,辛海华,邓永福,厉智强
(北京宇航系统工程研究所,北京100076)
最优区域划分的飞行器视觉测量标记
姜 威,辛海华,邓永福,厉智强
(北京宇航系统工程研究所,北京100076)
针对现有标记无法适应回转体飞行器曲面结构的问题,提出了最优区域划分的飞行器视觉测量标记设计方法。该方法首先根据飞行器截面成像模型将飞行器划分为6个子区域,保证飞行器成像中始终有一个完整的子区域;然后将子区域作为标记基本单元并将区域顶点作为标记点,在标记点满足共面约束的同时使点间的距离最大;最后根据颜色分布特性为子区域设计标识码,实现子区域之间的区分。仿真实验结果表明,当飞行器处于摄像机视场内时,标记成像中始终有一个完整的子区域,在子区域上能提取4个共面特征点用于飞行器位姿参数的准确解算。设计的曲面标记能够满足回转体飞行器(如炮弹弹丸、导弹等)视觉测量的要求。
兵器科学与技术;飞行器;位姿测量;视觉测量;标记
0 引言
视觉位姿测量是飞行器(如弹丸、导弹等)研制和试验过程中获取位姿参数重要手段[1-3]。飞行器上的自然特征定位精度不高[4-6],为提高视觉位姿测量精度,需要在飞行器上设计标记。
依据标记附着的物体结构进行划分,标记可分为平面标记与曲面标记。其中,平面标记最为常见[7-8],如文献[8]设计了一种由黑白矩形组成的标记,用于无人机自主着陆姿态的测量,但平面标记无法适应飞行器的曲面结构。
曲面标记相关研究很少,仅发现文献[9]及文献[10]针对锥形结构飞行器开展标记设计。文献[9]将棋盘格标记进行变形使其适应了锥形结构,文献[10]将锥面划分成若干个扇区并根据扇区开展特征优化设计,这些锥形标记难以适用于其它曲面结构的飞行器。针对现有标记无法适应飞行器曲面结构的问题,本文不失一般性的假设飞行器具有回转体结构,提出最优区域划分的飞行器视觉测量标记设计方法。
1 飞行器位姿单目视觉测量系统
图1为飞行器位姿单目视觉测量系统示意图。各坐标系定义为:图像坐标系oI-uIvI,坐标系原点oI在图像左上角,uI轴沿图像的行向右,vI轴沿图像的列向下;摄像机坐标系oc-xcyczc,坐标系原点oc在摄像机光心上,xc轴为摄像机水平轴,方向朝右,yc轴为摄像机竖直轴,方向朝下,zc轴沿摄像机光轴的反方向;飞行器坐标系op-xpypzp,坐标系原点op在飞行器底面中心,xp,yp轴沿底面圆的半径且相互垂直,zp轴沿弹轴并朝向飞行器顶点。

图1 飞行器位姿单目视觉测量系统Fig.1 Projectile monocular pose estimation system
假设飞行器上有n个标记点Pi,它们在图像坐标系中的坐标为PIi,在摄像机坐标系中的坐标为Pci,在飞行器坐标系中的坐标为Poi。由摄像机成像模型及刚体运动方程得
PIi=MPci,Pci=RPoi+T,
(1)
式(1)中,M为摄像机内参数矩阵;R为飞行器坐标系相对于摄像机坐标系的旋转矩阵;T为飞行器坐标系相对于摄像机坐标系的位移向量。
M由摄像机标定得到,PIi由标记点提取得到,Poi为已知量。根据文献[11],当n≥3且标记点不完全共线时能够解算出相对位姿参数R,T。
2 标记设计
2.1 子区域划分
当飞行器处于不同位姿时,摄像机只能拍摄到飞行器的部分表面。为保证标记成像中至少有3个标记点,将飞行器表面进行区域划分:首先将飞行器表面划分成一定数量的子区域,保证飞行器在不同的姿态下至少有一个完整的子区域被摄像机拍摄到;然后在每个子区域内至少设计3个标记点,保证标记成像中始终有足够多的标记点。为实现子区域的最优划分,建立如图2所示的飞行器成像模型。
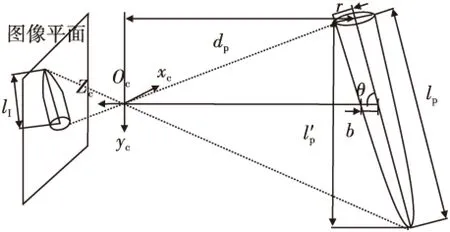
图2 飞行器单目视觉成像模型Fig.2 Monocular imaging model for projectile
(2)
(3)
式中:f为摄像机的焦距,dp为摄像机光心oc与飞行器轴线最近的水平距离。
当θ=90°时,式(3)中的等号成立。当θ∈(0,30°)∪(150°,180°)时,式(3)可改写为:
(4)
根据式(4),当θ∈(0,30°)∪(150°,180°)时,飞行器成像长度lI不到θ=90°时的1/2;此时飞行器成像的形变量很大,设计在飞行器表面的标记的可能会产生畸变,从而使标记点无法准确提取。为此在θ∈[30°,150°]范围内设计标记,使其结构成像清楚;当θ=30°(或θ=150°)时,标记成像在θ∈[30°,150°]范围内形变量最大。
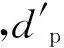
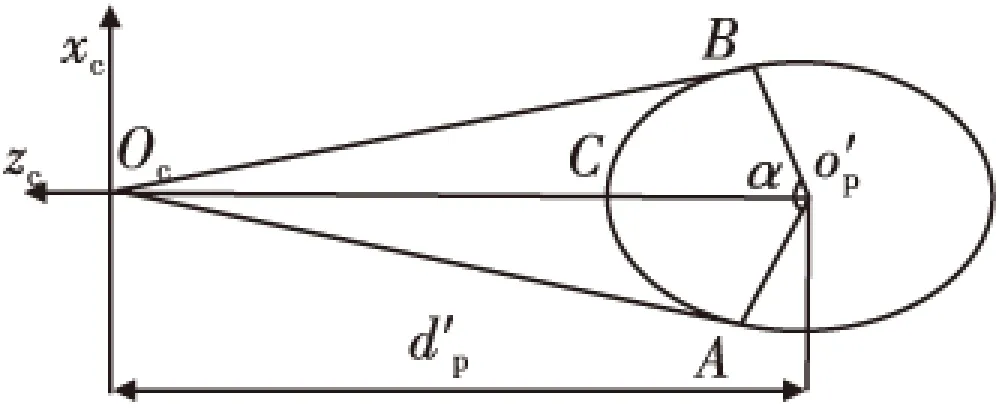
图3 飞行器截面单目成像模型Fig.3 Projectile section’s monocular imaging model
将椭圆按圆心角等分成n段,并使每个椭圆弧段对应的圆心角β满足β≤0.5α,以保证飞行器在绕飞行器轴线旋转时,始终有一个完整的椭圆弧段能被摄像机拍摄到。
下面计算α确定椭圆最优的分段数。由图2可得出椭圆短轴a和长轴b分别为
a=r,b=r/sinθ
(5)
式(5)中,r为飞行器半径。
点B在oc-xczc中的坐标(xb,zb)满足
(6)
式(6)中,k表示切线ocB的斜率。
由于B是椭圆截面与ocB切点
进而解得α
(7)
根据式(7),α与sinθ单调性相同。当θ=30°(或θ=150°)时,α在θ∈[30°,150°]范围内取得最小值为:
(8)
椭圆分段数n越大,飞行器表面划分就越细,标记点间距就越小;而标记点间距越小,系统对姿态角的分辨能力越低[12],标记点可区分性越差。在能满足椭圆分段要求的条件下,n越小越好;而n=6是n能满足分段要求的最小值。因此n取6,即将椭圆等分成6个椭圆弧段。
如图4所示,将飞行器所有横截面均按圆心角等分成6个椭圆弧段,即将飞行器表面等分成6个子区域并使子区域的边界与弹轴共面。
图4中,当飞行器处于不同姿态且θ∈[30°,150°]时,总有一个完整的子区域能被摄像机拍摄到。若再在每个子区域内至少设计3个标记点就可以保证标记成像中始终有足够多的特征信息。
2.2 共面标记点设计
根据文献[13]对PnP问题解唯一性的分析,若已知刚性被测目标上4个共面特征点的物理坐标和图像坐标,能解得目标位姿参数的唯一解。据此在每个子区域内设计4个共面标记点,以满足解算飞行器位姿参数的要求。如图5所示,为保证标记点共面,将标记点分别设计在两个垂直于弹轴的截面圆上。

图4 飞行器子区域划分Fig.4 Dividing projectile’s surface into 6 sub-regions

图5 共面标记点设计Fig.5 Designing coplanar points
图5中面ABC与面A′B′C′是垂直于弹轴AA′的截面,为保证标记点B,C,B′,C′共面,应使线BB′,CC′分别与弹轴AA′共面。
证明如下:
1)若两截面圆半径相同,则有BB′//AA′,CC′//AA′,因此标记点B,C,B′,C′共面。
2)若两截面圆半径不相同,由于线BB′、CC′均与弹轴AA′共面,则BB′延长线与弹轴AA′交于D,CC′延长线与弹轴AA′交于D′。根据三角形相似性有
由于
AB=AC=r1,A′B′=A′C′=r2
(9)
式(9)中,r1,r2分别为两个截面圆的半径。
即
可得
A′D′=A′D。
D′、D两点重合,即线BB′、CC′相交于D(D′)。两相交直线必然共面,所以标记点B,C,B′,C′共面。
如图6所示,由于子区域侧边与飞行器轴线共面,用两个垂直于飞行器轴线的截面将子区域分成三段,保留中间部分,这部分的4个顶点即可作为标记点。图中标记点位置用黑色“×”标出。

图6 共面标记点Fig.6 Coplanar points
为增加标记点间的距离,保留的子区域应尽量位于飞行器中直径较大的部分,且标记点沿弹轴方向的距离应当足够大。
2.3 标记标识码设计
要完成标记点匹配应使每个标记点都具有唯一可识别性。可将子区域涂成不同颜色,但这种方式容易受外界条件干扰。本文通过在子区域内设计小区域方式完成标识码设计:首先将标记颜色设计成白色和黑色,这两种颜色具有最强的对比度;然后在每个子区域内设计0~2个的小区域;最后根据子区域颜色及小区域数量给每个子区域设计唯一标识码,如图7及表1所示。
标记点匹配时,先利用标识码识别子区域,再根据标记点在子区域内的位置识别标记点。

图7 子区域标识码设计Fig.7 Designing code for sub-regions

序号子区域123456标识码000110001100010101
注:标识码第1位代表子区域颜色,黑色为0,白色为1;标识码第2、3位代表小区域数量,没有小区域为00,含1个小区域为01,含2个小区域为10。
3 仿真实验
为验证标记是否满足飞行器位姿单目测量要求,对不同位姿的飞行器进行仿真实验。仿真对象为用3D MAX软件生成的常规飞行器模型(长度550 mm、弹径100 mm)。摄像机为3D MAX软件默认的135相机,设置摄像机视场角为30°,图像分辨率为640×480。
在飞行器表面涂上所设计的标记,给飞行器模型设置不同的位姿并生成图像。图8给出了飞行器在不同极限位置下的成像,图8(a)是飞行器轴线与光轴夹角为30°时的飞行器成像,此时标记成像的形变量最大,标记最容易产生畸变;图8(b)是摄像机能够同时拍摄到两个完整的子区域时飞行器的成像,此时子区域外侧成像的形变量最大;图8(c)是飞行器在离摄像机10 m时的成像,此时飞行器与摄像机距离较远,标记成像的像素数量很少,可能导致标记点无法区分;图8(d)是飞行器在一般姿态下的成像。图8涵盖了标记成像的所有极限位置,如果标记成像始终清楚,则表明标记能够满足位姿测量要求。

图8 飞行器在不同位姿下的成像Fig.8 Projectile images in different pose
图8中标记点位置已用黑色“×”标出。由图8可见,当飞行器处于不同位姿时,图像中至少有一个含有4个共面标记点的完整的子区域。图8(a)中标记结构清楚,各部分没有发生畸变,标记点能区分开;图8(b)子区域外侧成像清楚,标记点位置能准确提取;图8(c)在远距离时,标记结构清楚,标记点没有重合到一起;图8(d)中标记上有一个子区域且标记点成像清楚。因此当飞行器在处于极限位置时,标记没有出现畸变,标记点成像清楚且能准确提取。
将所设计的标记用于飞行器位姿解算,给飞行器设置不同的位姿并生成图像。表2为飞行器的6组位姿参数,这6组位姿涵盖了标记成像的不同极限位置:第1组,飞行器轴线与摄像机光轴夹角为30°(对应图8(a)),标记成像的形变量最大;第3组,摄像机恰好能拍摄到两个子区域,子区域外侧成像的形变量最大(对应图8(b));第2组到第3-第6组为普通位姿;每组位姿下,沿摄像机光轴方向每间隔100 mm生成一幅图像,每组位姿参数均包括远近不同的距离。

表2 飞行器位姿参数
提取图像中的标记点,根据文献[11]提供的方法初步解算飞行器位姿参数,然后用文献[12]给出的平差法进行优化。将解算结果与设定值比较得到误差,计算误差绝对值并求均值结果见表3。
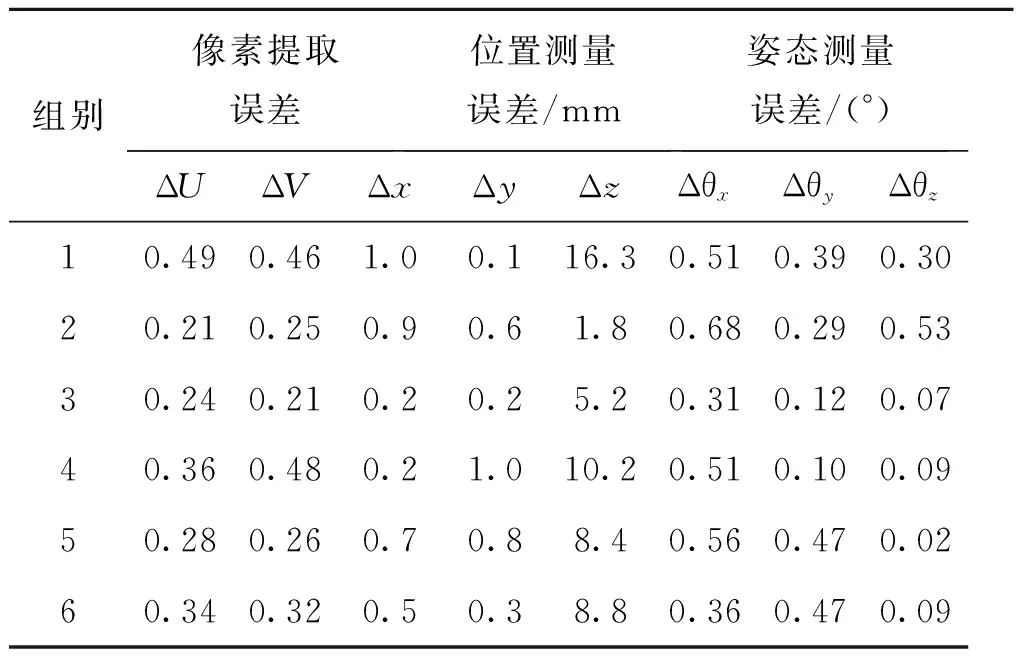
表3 标记点提取误差及飞行器位姿测量误差
由表3可以看出,无论是极限位姿还是任意位姿下标记点的像素定位误差均不超过0.5个像素,这进一步说明标记在各种姿态下没有发生畸变,标记点定位准确。在相应的像素提取精度下,位置测量精度在摄像机xc,yc轴方向上误差小于1 mm,zc轴方向上误差小于16.3 mm;姿态角误差在3个轴方向上分别小于0.68°,0.47°,0.53°。
根据仿真实验, 当飞行器处于不同的位姿时,摄像机始终能在标记上拍摄到4个清晰的共面标记点,利用标记点能解算出飞行器位姿参数且精度较高。
4 结论
本文提出了最优区域划分的飞行器视觉测量标记方法。该方法先将飞行器表面划分成6个子区域,将子区域作为标记设计基本单元;然后在基本单元内规划标记点分布位置使其满足共面约束且分布位置最优;最后基于区域灰度分布特征给子区域设计标识码。仿真实验结果表明,标记成像中始终有一个完整的子区域,在子区域上能提取4个共面特征点,能够满足飞行器位姿单目视觉测量的要求。该标记能够用于各种具有回转体结构的飞行器,也可以用于其他具有类似结构的目标。
[1]Nagarkar Vivek V, Singh Bipin, Miller Stuart, et al.A modular high precision digital system for hyperveloci- ty projectile performance measurements [C]//Visual Information Processing XVII. Florida, USA, 2008: 801-808.
[2]Herrejon R, Kagami S, Hashimoto K.Online 3-D trajectory estimation of a flying object from a monocular image sequence [C]//IEEE/RSJ Interna tional Conference on Intelligent Robots and Systems.St.Louis, USA, 2009: 2496-2501.
[3]秦晓燕, 王晓芳, 陈萍, 等.基于Adaboost算法的炮弹炸点检测 [J].兵工学报, 2012, 33(6): 682-687.
[4]Ribnick Evan, Atev Stefan, Nikolaos P.Papanik- olopoulos.Estimating 3D positions and velocities of projectiles from monocular views [J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(5): 938-944.
[5]于起峰, 孙祥一, 陈国军.用光测图像确定空间目标俯仰角和偏航角的中轴线法 [J].国防科技大学学报, 2000, 22(2): 15-19.
[6]Zhao Zhuxin, Wen Gongjian, Zhang Xin, et al.Model-based estimation for pose, velocity of projectile from stereo linear array image [J].Measurement Science Review, 2012, 12(3): 104-110.
[7]Mark Fiala.Designing highly reliable fiducial markers [J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(7): 1317-1324.
[8]Mondragon Ivan F, Pascual Campoy, Carol Martnez, et al.3D pose estimation based on planar object tracking for UAVs control [C]//IEEE International Conference on Robotics and Automation, Alaska, USA.IEEE, 2010: 35-41.
[9]李蒙, 谌德荣, 周广铭, 等.用于圆锥体位姿测量的曲面标记[J].中国图象图形学报, 2012, 17(12): 1534-1539.
[10]李蒙.圆锥体飞行目标位姿测量特征标记设计[D].北京:北京理工大学, 2012.
[11]赵锐.基于单目视觉的物体位姿测量方法研究 [D].合肥: 合肥工业大学, 2005.
[12]尚洋.基于视觉的空间目标位置姿态测量方法研究 [D].长沙: 国防科学技术大学, 2006.
[13]胡占义, 雷成, 吴朝福.关于P4P问题的一点讨论 [J].自动化学报, 2001, 27(6): 770-776.
Optimal Region Dividing Marker for Projectile Pose Estimation
JIANG Wei, XIN Haihua, DENG Yongfu, LI Zhiqiang
(Beijing Institute of Astronautical Systems Engineering, Beijing 100076, China)
A vision measuring marker was designed for monocular pose estimation of target with revolved body, i.e. projectile. At first, the projectile surface was divided into 6 equal sub-regions to guarantee that there was always a complete sub-region in projectile’s image according to the imaging model. Then, the 4 vertexes of each sub-region were used as a set of marker points, which were coplanar and the distances between which were maximized. At last, the sub-regions could be distinguished using their color distribution, based on which a unique code was assigned to each sub-region. Experimental results using simulation image showed that: a set of 4 marker points could be detected and used to calculate the projectile’s pose accurately, under the situation that the projectile was caught by the camera. The proposed marker could be applied to various targets with revolved body, such as bullets, shells, missiles, etc.
armament science and technology; projectile; pose estimation; vision measurement; marker
2016-11-03
姜威(1986-),男,河南信阳人,硕士,工程师,研究方向:运载火箭电气系统总体设计。E-mail:240884664@qq.com。
TP751.1
A
1008-1194(2017)02-0115-05

